JUMP TO TOPIC
Rational Expression|Definition & Meaning
Definition
A rational expression is a fraction whose numerator and denominator are polynomials. Just like its name, The ratio of two polynomials is named the rational expression.
When f is an expression that is rational then it can also be noted in the form, x/y where x and y are polynomials. Basic arithmetic operations like subtraction, addition, multiplication, and division can be done on rational expressions just like polynomials or any other expression.
A good principle of rational expressions is that when any of the above-mentioned operations are performed on two rational expressions, the result is always a different rational expression. Unlike polynomials, rational expressions are normally easy to multiply or divide but relatively harder to add or subtract. An example is given below.
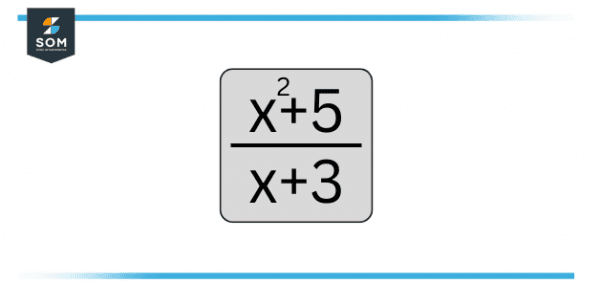
Figure 1 – Rational Fraction Example
What Is a Rational Expression?
You would have studied rational numbers, which are written in the form of p/q. But on the other hand, Rational expressions are the ratio of two polynomials.
We have to put the polynomial expression equal to zero in order to find the root or zero of the expression. But if one desires to figure out the zeros of rational expressions, only the numerator should be made zero when the expression is reduced to its lowest term.
The lowest terms indicate that numerator and denominator both don’t have even a single factor in common. Like when we talk about a fraction, then 4/16 is not in the lowest form of the expression. It can be reduced even further by taking 2 as a common factor. Finally, 1/4 is the lowest form.
Likewise, for example, $\mathsf{\dfrac{x^2+2x}{3x}}$ which is a rational expression, but it is not in its lowest form. So again if we take the common factor x from both the numerator and denominator, we get $\mathsf{\dfrac{x+2}{3}}$, which is now the lowest form of the expression.
Rational Expressions Simplification
Some significant points to memorize for performing arithmetic operations on rational fractions are listed below. These operations include addition, subtraction, division, and multiplication.
Figure 2 – Arithmetic Operation for Simplifying Rational Expression
When getting rational expressions to a reduced form, the basic and most important step is to factor both the numerator and the denominator. And then, cancel out the common factors of the expressions.
Addition and Subtraction
In solving Rational expressions, if the fraction has the same polynomial in the denominator, then add or subtract the numerators while keeping the denominator unchanged. then if possible, further reduce the expression.
If the denominators of a rational expression are not the same, the first step should be taking the LCM. Now, make each rational expression equal by making the denominator of all expressions identical. In the final step, Add or subtract the terms, then if possible, further reduce the expression.
Multiplication
Factorize the polynomials in fractions (Numerator and Denominator), then reduce wherever possible. Multiplying the remaining numerators and denominators separately will result in a reduced form.
Division
Multiply the inverted denominator with the first rational expression (i.e., numerator) because reduction is much easier after converting the division into multiplication by inverting the denominator, just like in the case of dividing fractions. As explained above, further simplification is identical to multiplication.
Addition and Subtraction of Rational Expressions
As we already know, for adding or subtracting any two fractions, the denominator should be the same for both fractions. The same rule is functional to rational functions too. Normally, the given formula is how we represent addition and subtraction:
\[ \mathsf{\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}} \]
\[ \mathsf{\dfrac{a}{c} – \dfrac{b}{c} = \dfrac{a-b}{c}} \]
Assuming a fraction. For example, add and subtract 2/3 and 1/2.
So first, adding both fractions, we get:
\[ \mathsf{\dfrac{2}{3} + \dfrac{1}{2} = \dfrac{4+3}{6} = \dfrac{6}{6}} \]
Now by subtracting 1/2 from 2/3, we get:
\[ \mathsf{\dfrac{2}{3} – \dfrac{1}{2} = \dfrac{4-3}{6} = \dfrac{1}{6}} \]
In the above steps, you can see that we take the LCM first to make the numerators identical, and once the expressions are normalized, we perform the operations.
Multiplication and Division of Rational Expressions
Just like we added and subtracted rational functions, we can multiply and divide them too. The general formula is:
\[ \mathsf{\dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{ac}{bd}} \]
\[ \mathsf{\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{ad}{bc}} \]
The Rule for Rational Fraction
We need to address the unspoken rule of dealing with rational expressions. We know that division of a number by zero isn’t permitted. The same practice is followed for rational expressions. With rational expressions, we will always take the values for X that won’t give a division by zero. We sometimes note these restrictions down, but we will always need them to be memorized.
\[ \mathsf{\dfrac{2}{x-2} \hspace{0.5cm};\hspace{0.5cm} \dfrac{y^2 -1}{y^2+5} \hspace{0.5cm};\hspace{0.5cm} \dfrac{z^4 + 18z + 1}{z^2 – z – 6}} \]
In the first one listed above, we cannot take x=2. The second rational expression can not be zero in the denominator, so we don’t have to stress about any restrictions. Also, note that the second rational expression’s numerator will be zero, which is acceptable if we avoid division by zero.
Now, for the third rational expression, we will have to avoid m = 3 and m = −2. The final rational expression given above can never be zero in the denominator, so we don’t need to have any limitations.
Simplifying Rational Expressions
The quotient of 2 polynomial expressions is the rational expression. Now the properties of fractions will also apply to rational expressions, just like reducing the expressions by cutting common factors from the numerator and the denominator. To be able to do this, first of all, we have to factor in the numerator and denominator. Let’s begin with the rational expression given below:
\[ \mathsf{\dfrac{x^2 +8x + 16}{x^2 + 11x + 28}} \]
Factorizing the numerator and denominator and rewriting the expression:
\[ \mathsf{\dfrac{(x + 4)^2}{(x + 4) (x + 7)}} \]
By canceling out the common values, we can solve the expression factor (x+4) as:
\[ \mathsf{\dfrac{x+4}{x+7}}\]
Example of Solving a Rational Expression
Simplify the given expression:
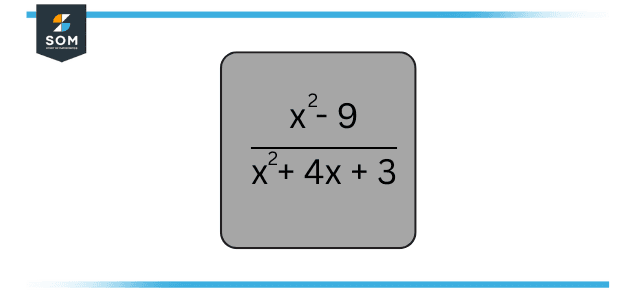
Figure 3 – Simplifying Rational Expression
Solution
The common factor can be canceled because 1 is the result when any expression is divided by itself.
\[ \mathsf{\dfrac{(x+3) (x-3)} {(x+3) (x+1)}} \]
\[ \mathsf{\dfrac{x-3} {x+1}} \]
All images/mathematical drawings were created with GeoGebra.
