Sequence|Definition & Meaning

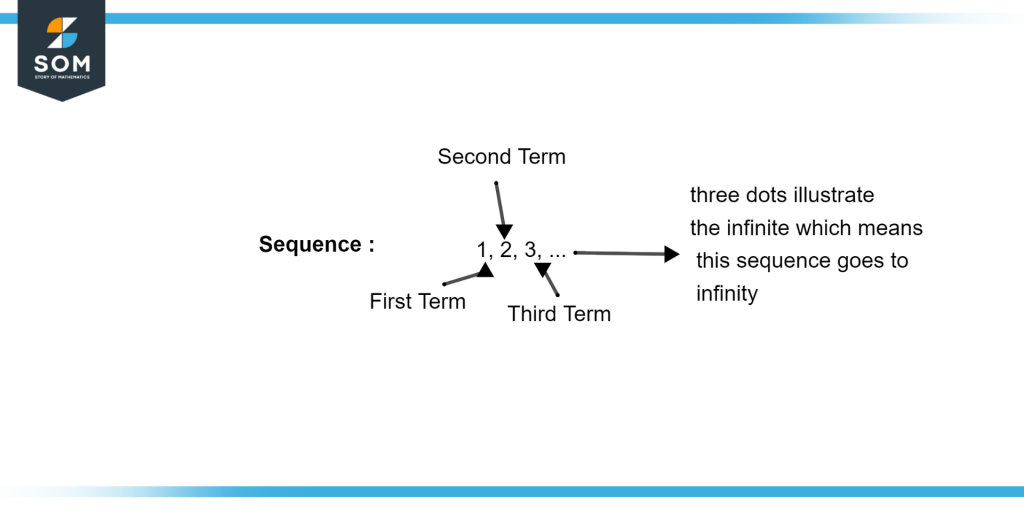
Figure 1 – Sequence

Figure 1 illustrates a sequence with its specifications. 

An enumerated collection of things in mathematics known as a sequence allows repeats and emphasizes the importance of order. It possesses members, much like a set (also called elements or terms).

The length of the series is the number of items in it, which might be infinite. The order of the components in a sequence does matter, unlike a set, and the same elements might occur in a sequence numerous times at various points.

A sequence is formalized as a function from natural numbers (the locations of sequence members) to the items at each place. An indexed family, which is a function from any index set, can be thought of as a sequence in the broadest sense. For instance, the letters (M, A, R, Y) are arranged from first to last, with M being the first letter.

This pattern is distinct from (A, R, M, Y). Furthermore, the sequence (1, 1, 2, 3, 5, 8), which includes the number 1 in two separate locations, is a legitimate sequence. Sequences may be endless or finite, as in the case of the series of all even positive integers (2, 4, 6, ...).

In computer science and computers, finite sequences are frequently referred to as strings, words, or lists; these names typically correlate to various ways that they might be represented in computer memory. Infinite sequences are referred to as streams. Most concepts of the sequence include the empty sequence (). However, this might vary depending on the situation.

The quantity of words in a sequence is what determines its length. An n-tuple is another name for a sequence of length n. The element-free empty sequence () is one example of a finite sequence. In most cases, when someone uses the word “infinite sequence,” they’re referring to a sequence that contains a start element, but no end element is infinite in one direction and finite in the other.

When disambiguation is required, this type of sequence is referred to as a singularly infinite sequence or a one-sided infinite sequence. A bi-infinite sequence, two-way infinite sequence, or twice infinite sequence is, on the other hand, a sequence that is infinite in both directions—that is, it contains neither a start nor a final element.

Increasing and Decreasing Sequence

Each term in a series must be bigger than or equal to the one before it in order for it to be considered to be monotonically rising. If each next term rigorously exceeds (>) the one before it, the sequence is said to be strictly monotonically rising.

Every subsequent term in a series must be smaller than or equal to the one before it to be considered monotonically decreasing; otherwise, it is strictly monotonically decreasing. A series is referred to as monotone if it is either rising or decreasing.

Sub-sequence

A sub-sequence of a given sequence is a sequence that is created from the provided sequence by removing some of the items while maintaining the relative locations of the remaining elements.

For example, the positive even integer sequence (2, 4, 6,…) is a sub-sequence of the positive integers (1, 2, 3, …). Some pieces move into other locations because of the removal of other ones. The relative positions, however, are kept.

Types of Sequences

An arithmetic sequence is one in which each word is produced by either increasing or decreasing the preceding number by a specific amount.

A geometric sequence is one where each phrase is produced by multiplying or dividing a certain integer by the one before it. If the reciprocals of every number in a sequence form an arithmetic sequence, the numbers are said to be in a harmonic sequence. The Fibonacci sequence, which begins with 0 and 1, is an intriguing collection of numbers where each element is created by adding two components that came before it.

If the difference is constant in the sequences, then the sequence is arithmetic, and if the difference is not constant, then the sequence is quadratic.

Difference Between Series and Sequences

In sequence group of components is with a pattern. The order of the components matters. Finite order: 1, 2, 3, and 5. Indefinite succession: 1, 2, 3, 4. A series is the sum of the sequence’s component parts. The order of the components is not as crucial in series. Finite series: 1, 2, 3, 4, and 5. Numerous Series: 1+2+3+4+.

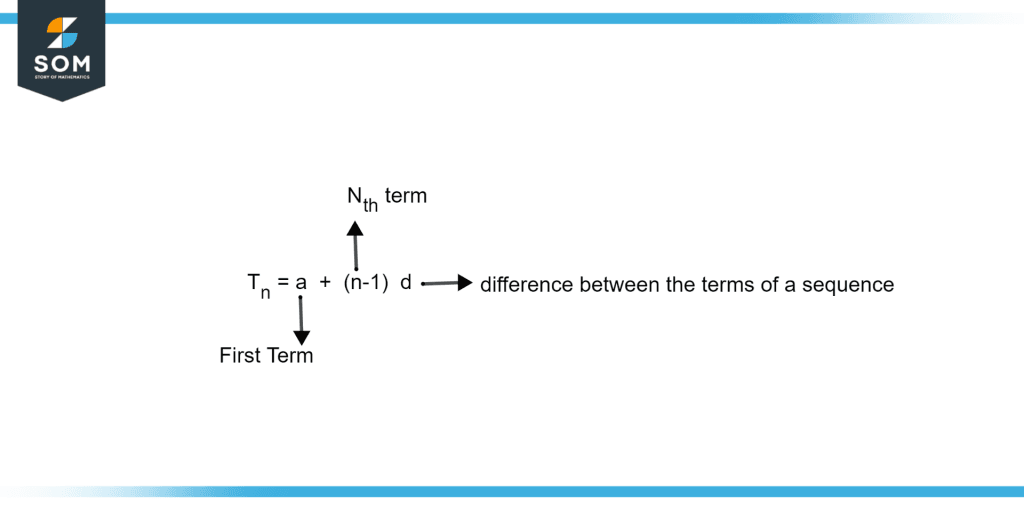
Figure 2 illustrates the formula to find the n-th term in the sequence where a is the first term of the sequence, n is the index of the term want to find, and d is the difference between the terms of a sequence.

Some Examples of Sequences

Example 1

Illustrate the Geometric sequence on the real line with a common multiple of three up to four terms.

Solution

As we want to illustrate the sequence on the real line so we will draw a real line and start from one. As we have a common multiple of three so we will multiply by three up to four terms, as illustrated in figure 3.

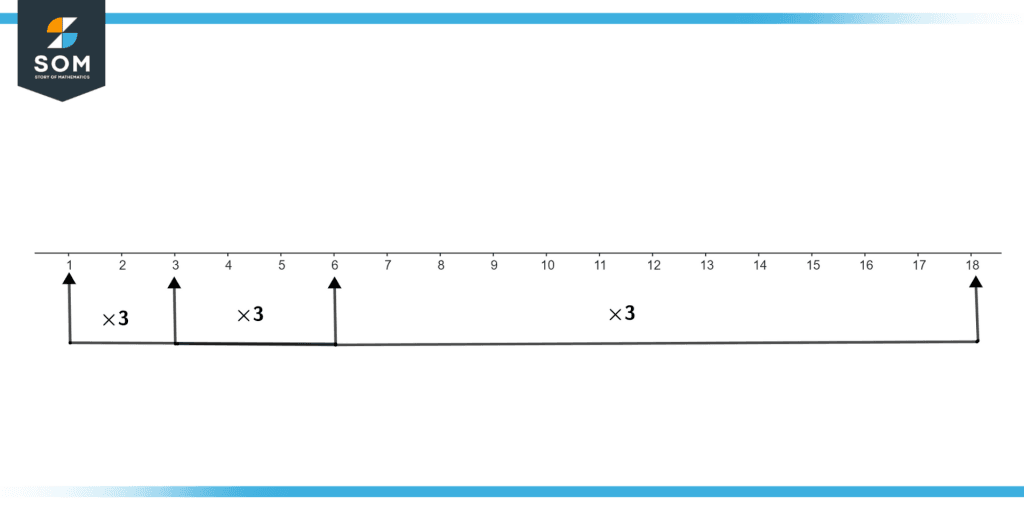
Figure 3 – Geometric-Sequence

The sequence will be 1,3,6,18.

Example 2

Find the common difference and 20^th term of the following sequences.

a) 4,7,10,13, …

b) 2,4,6,8,10,…

c) 3,6,9,12,15,…

Solution

a) In order to compute the difference, we have to subtract the first term and second term:

7 – 4 = 3

So the difference is three. In order to compute the n^th term, we have the formula:

$T_n$ = a + (n-1) $\times$ d

$T_n$ = 4 + (20-1)$\times$3

$T_n$ = 4 + 19$\times$3

$T_n$ = 61

So the 20^th term of the sequence is 61.

b) In order to compute the difference, we have to subtract the first term and second term:

4 – 2 = 2

So the difference is three. In order to compute the n^th term, we have the formula:

$T_n$ = a + (n-1) $\times$ d

$T_n$ = 2 + (20-1)$\times$2

$T_n$ = 2 + 19$\times$2

$T_n$ = 40

So the 20^th term of the sequence is 40.

c) In order to compute the difference, we have to subtract the first term and second term:

6 – 3 = 3

So the difference is three. In order to compute the n^th term, we have the formula:

$T_n$ = a + (n-1) $\times$ d

$T_n$ = 3 + (20-1)$\times$3

$T_n$ = 3 + 19$\times$3

$T_n$ = 60

So the 20^th term of the sequence is 60.

All images were created using GeoGebra.

Septagon Definition < Glossary Index > Si Units Definition