SI Units|Definition & Meaning

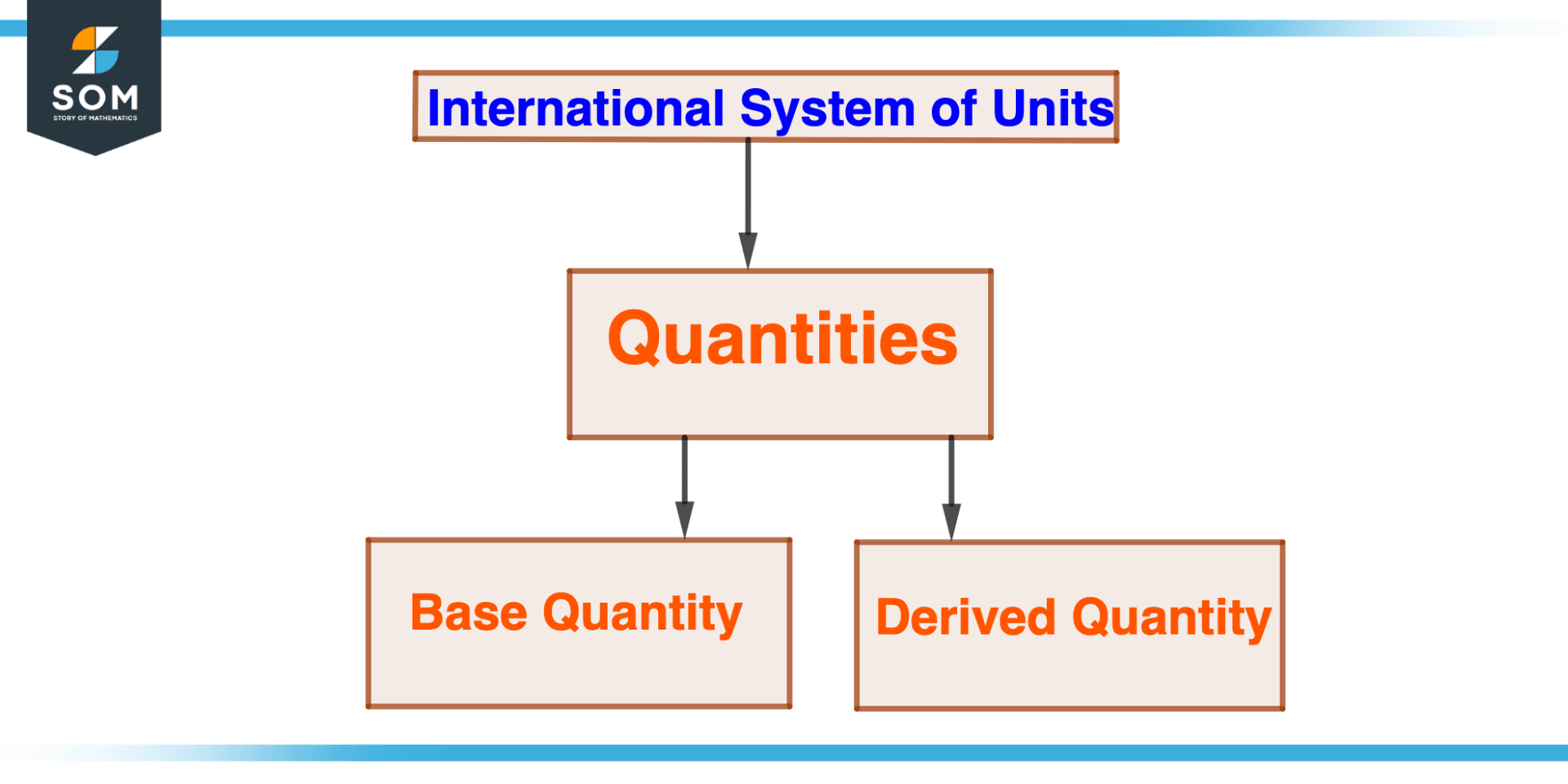
Figure 1 – Quantities in International system of units

Quantities can be divided into two groups in the International System of Units (SI): base quantities and derived quantities.

Base Quantity

The term “base quantity” refers to a quantity that cannot be defined in terms of another quantity. The SI system has seven fundamental units: length, mass, time, electricity, thermodynamic temperature, substance amount, and luminous intensity.

Derived Quantity

Quantities that can be defined in terms of one or more base quantities are referred to as derived quantities. For instance, velocity is a derived quantity representing the displacement of an object over time, and acceleration is another derived quantity defined as the rate of change of velocity over time. 

The derived quantities force, energy, power, and electric charge are additional examples. 

The flowchart of SI units is shown below.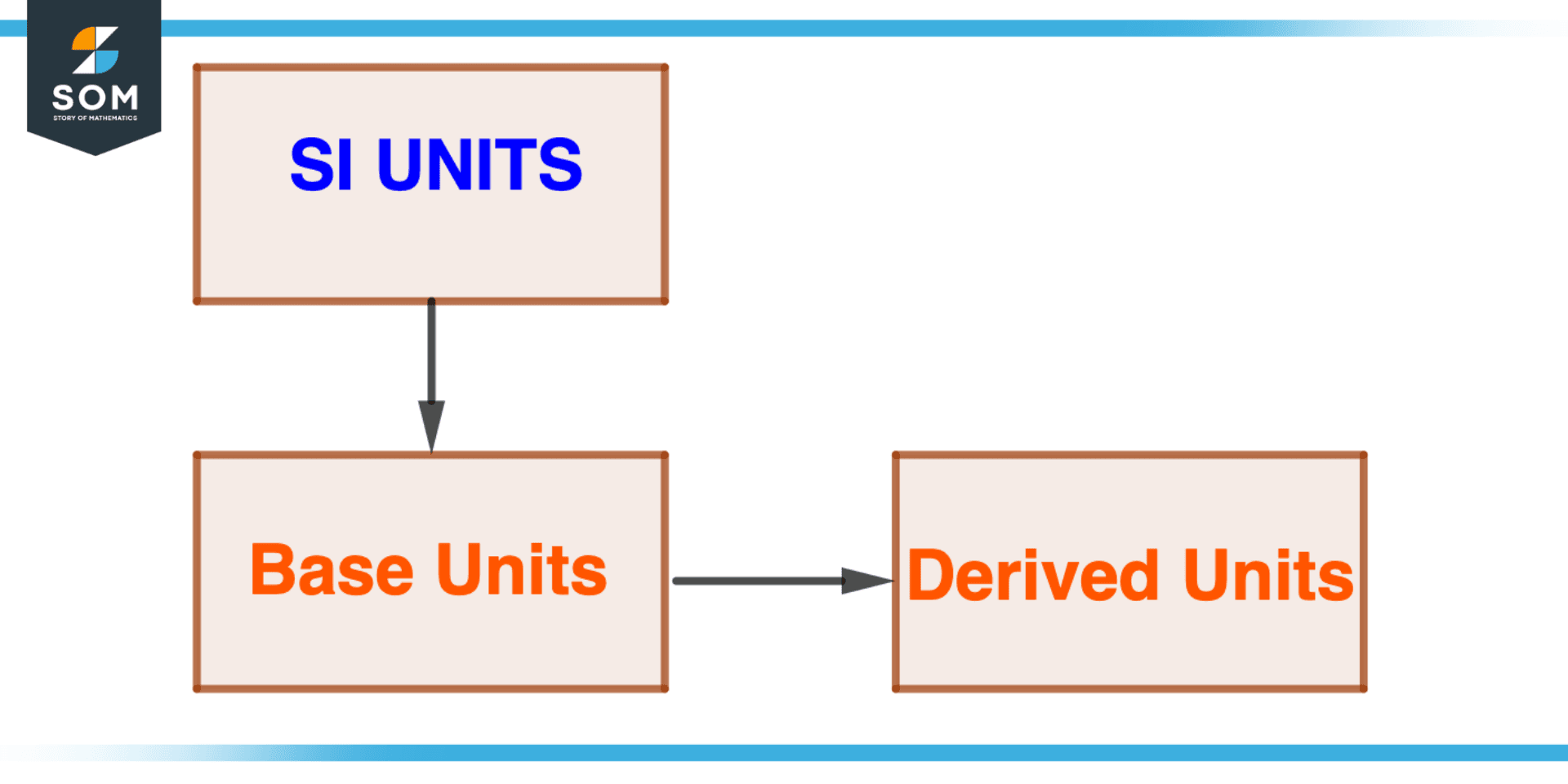

Figure 2 – Flow of Base Units and Derived Units

Base Units

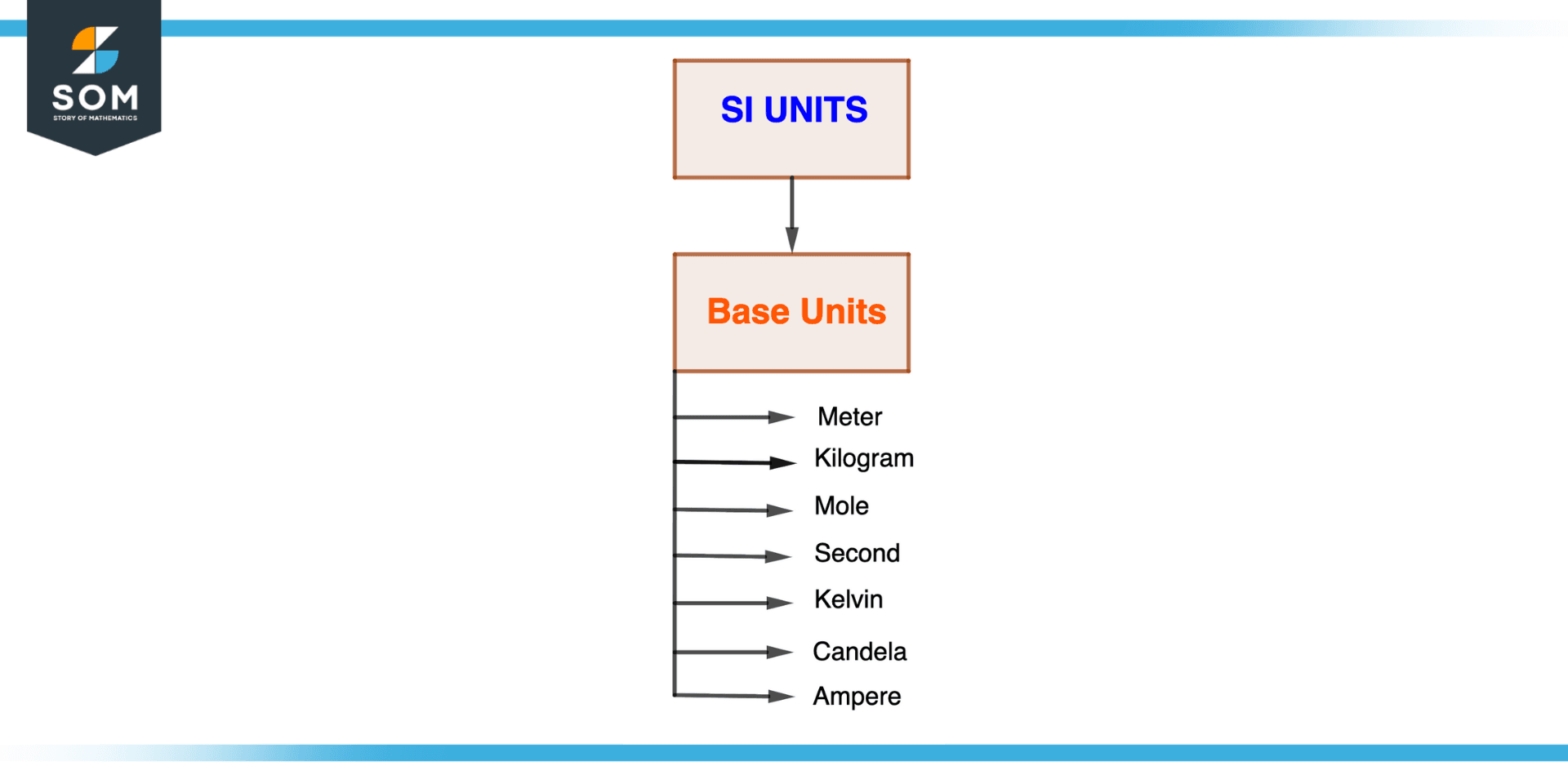
Figure 3 – SI Base Units

For a specific system of measurement, such as the metric or SI system, the base units are the accepted units of measurement (SI). The seven basic SI units are the meter (length), the kilogram (mass), the second (time), the mole (amount of substance), the kelvin (temperature), the ampere (electric current), and the candela (luminous intensity).

Here is a quick description of each.

Meter

The distance that light covers in a vacuum in 1/299,792,458 of a second is measured in meters, or m.

Kilogram

The kilogram (kg), the fundamental unit of mass, is defined as the weight of the platinum-iridium cylinder known as the International Prototype of the Kilogram, which is kept at the International Bureau of Weights and Measures.

Second

The duration of 9,192,631,770 radiation periods, or the base unit of time, the second, is equal to the change in the cesium-133 atom’s ground state between its two hyperfine levels.

Mole

The mole, or mol, is the basic unit of substance quantity and is the amount of a substance containing the same number of entities is described as there are in 12 grams of carbon-12.

Kelvin

The base unit of temperature is the kelvin (K), which is equal to 1/273.16 of the triple point of water’s thermodynamic temperature.

Ampere

The ampere (A), the fundamental unit of electrical current, is the constant current that, if maintained in two parallel, straight conductors of infinite length and negligible circular cross-section, spaced one meter apart in vacuum, would result in a force between these conductors equal to 2 x 10^-7 newtons per meter of length.

Candela

The candela (cd), the basic unit of luminous intensity, is defined as the amount of light emitted in a given direction by a source with a radiative intensity of 1/683 watt per steradian and a frequency of monochromatic radiation of 540 x 10¹² Hz.

Derived Units

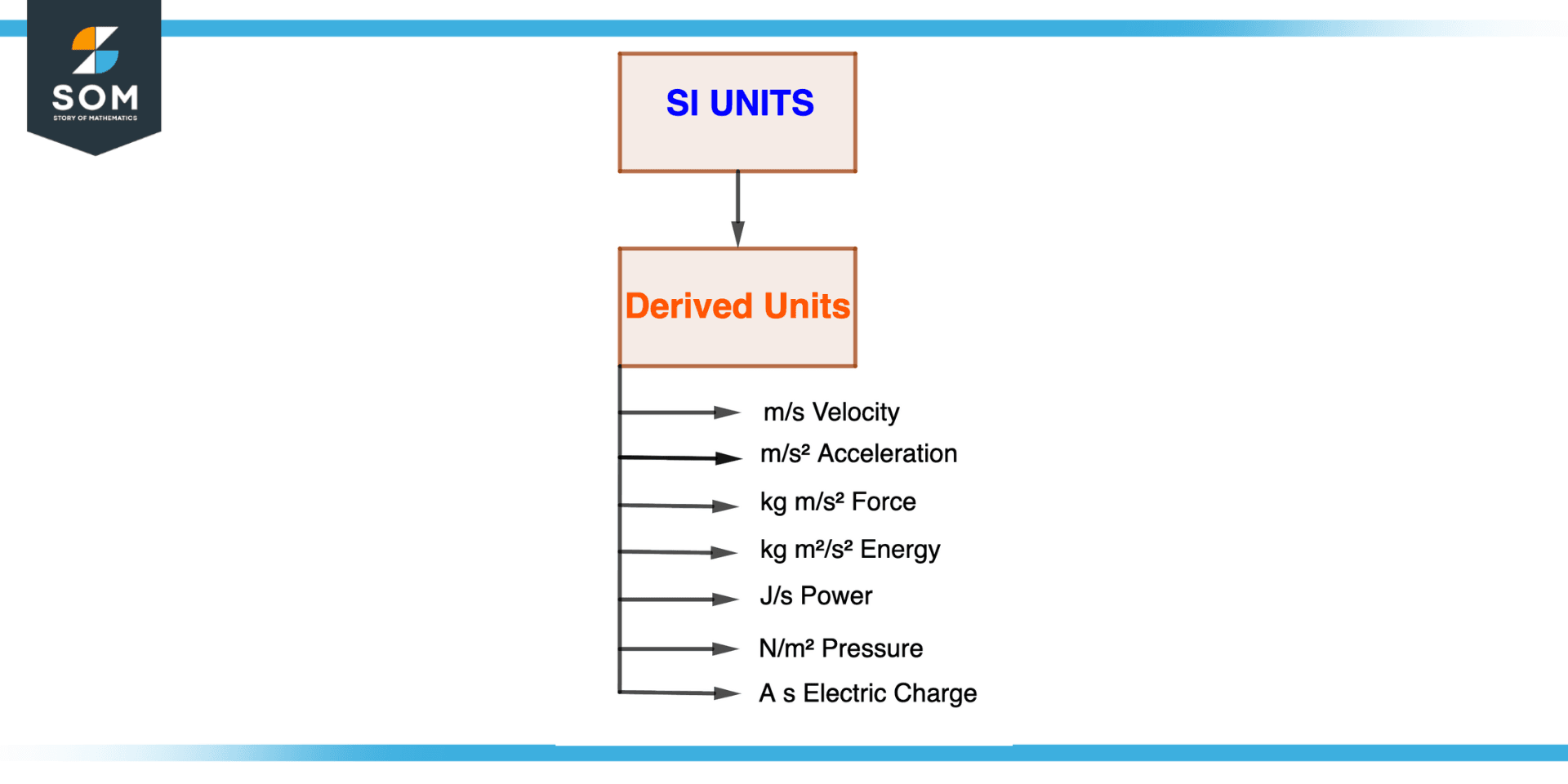
Figure 4 – SI Derived Units

Defined in terms of the base units of a specific system of measurement, such as the International System of Units, derived units are units of measurement (SI). Contrary to base units, derived units are defined in terms of combinations of the base units rather than having their own independent definition.

The following are some instances of derived SI units:

Velocity v = m/s

Acceleration a = m/s²

Force N = kgm/s²

Energy J = Nm = kgm²/s²

Power W = J/s 

Pressure Pa = N/m²

Electric charge C = As

Derived units offer a practical and standardized method of expressing various physical quantities, including speed, force, energy, power, and pressure, which are used to measure a wide range of physical quantities.

Significance of Learning SI Units

The most popular system of measurement in use today, the International System of Units (SI), offers a consistent and standardized method for measuring physical quantities. Learning SI units is crucial for the following reasons.

• Consistency: The use of SI units guarantees that measurements of physical quantities are uniform across nations and cultures, facilitating comparison and information exchange.
• Precision: The SI units have a precise definition, making it possible to make accurate measurements and lowering the chance of errors.
• Clarity: Using standardized units of measurement facilitates the comprehension and exchange of data and information in both academic and real-world settings.
• Applications in science: Since SI units offer a standard language for expressing and comparing measurements of physical quantities, they are crucial for scientific research.

International communication and collaboration in fields like science, technology, and business are made possible in large part by the use of SI units.

Applications of SI Units

Numerous scientific and technical applications employ the International System of Units (SI units), including.

• Physics: Physical quantities like length, mass, time, and energy are expressed using SI units.
• Chemistry: In chemical experiments and reactions, SI units are used to express quantities like concentration, volume, and temperature.
• Biology: In biological studies, SI units are used to express quantities like length, mass, volume, and time.
• Engineering: To design and measure structures, machines, and systems, SI units are used in engineering applications.
• Medicine: In medical diagnoses, treatments, and research, SI units are used to express quantities like length, mass, volume, time, and dose.
• Meteorology: In order to express atmospheric parameters like temperature, pressure, and wind speed, SI units are used.
• Astronomy: To express astronomical quantities like distance, mass, and time, SI units are used.

There are many other uses as SI units can be used to depict any quantity.

SI vs. MKS vs. CGS

SI

Despite being a contemporary and widely used system, the International System of Units isn’t the only one that has been applied to scientific and technical fields. The MKS (meter-kilogram-second) and CGS (centimeter-gram-second) units are two older systems.

MKS

The three base units of the SI system—the meter (length), kilogram (mass), and second (time)—are the foundation of the MKS system. The SI system has largely taken the place of the MKS system, which was widely used in the late 19th and early 20th centuries.

CGS

The centimeter, gram, and second units form the basis of the CGS system (time). In the 19th century, the CGS system was widely used to express electrical and magnetic quantities in physics and engineering.

An Example of SI Units Used To Derive Other Quantities

Consider the SI units of mass, length, and time: kilogram, meter, and second. Derive the units of velocity, acceleration, and force using them.

Solution

Velocity

Velocity is given by displacement over time. Displacement is essentially length. Therefore, we can say the units will be that of length over time, so meters/second is the unit of velocity, or m/s (meters per second).

Acceleration

Acceleration defines the rate at which velocity changes. This is given by dividing the velocity of an object by time elapsed. The combination of the units of velocity and time in the form of a fraction gets us: (meters/second) / second = meters / second², which is the unit of acceleration. We usually write it as m/s² (meters per second squared).

Force

Given that force is the product of mass and acceleration (F = ma), combining the units of mass and acceleration gets us the following result:

F = kg * m/s²

The unit kgms² or kgm/s², pronounced as kilogram meter per second squared, is also called and written as the newton or N (after the physicist Isaac Newton).

All mathematical drawings and images were created with GeoGebra.

Sequence Definition < Glossary Index > Side Definition