JUMP TO TOPIC
Side|Definition & Meaning
Definition
In two-dimensional flat shapes, a side is one of the various one-dimensional line segments bounding the shape. The sum of the length of all sides of a flat shape defines its perimeter. In 3D shapes, a side of the object is usually called a face instead, and each side of a 3D object is a flat 2D shape instead of a 1D line segment.
Figure 1 shows the three sides, AB, BC, and CA, of an equilateral triangle ABC.
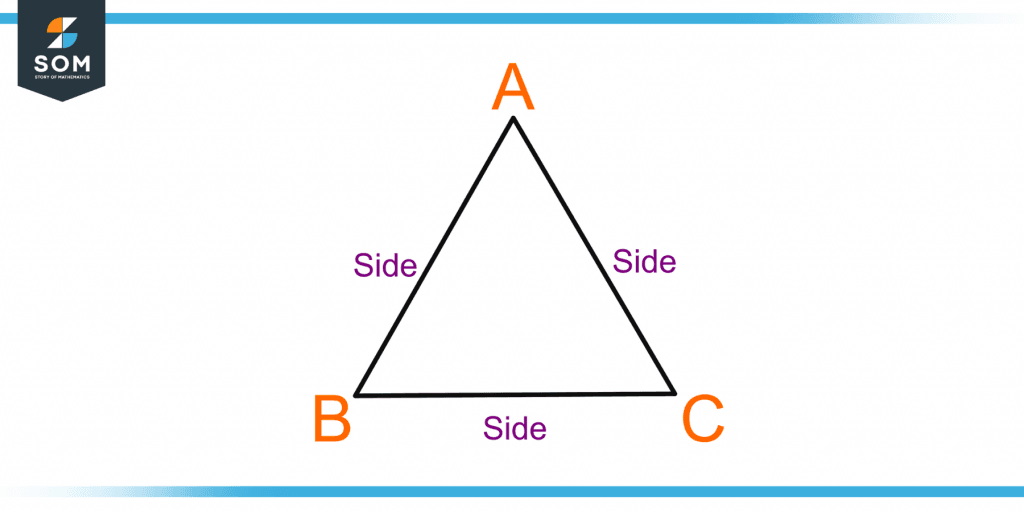
Figure 1 – Demonstration of Sides of an Equilateral Triangle
Polygon
A polygon is a closed two-dimensional shape on a plane or flat surface made with straight lines. These straight lines are the sides of the polygon, also known as edges. A polygon has no curved side. The corner points where two edges or sides meet are known as the vertices of a polygon.
Regular and Irregular Polygons
Regular polygons have all sides of equal length and equal internal angles. For example, an equilateral triangle is a regular polygon, as all its sides are equal, and all the internal angles measure 60°.
An irregular polygon either has sides of unequal length or unequal interior angles, or both. For example, a scalene triangle is an irregular polygon as it has three unequal sides.
Perimeter
A polygon’s perimeter is the total length of all the sides of a polygon. The perimeter’s unit is the same as the unit of the side’s length of the polygon.
Area
The area of a polygon can be found if the perimeter P and the apothem A of the polygon are known. The apothem is the length of the line segment from a midpoint of any side to the polygon’s center. Hence, the general formula for the area of a polygon is:
Area of a Polygon = (1/2)PA
Polygons With Different Numbers of Sides
The different types of polygons, depending on their number of sides discussed as follows:
Triangle
A triangle has three sides with three internal angles. The sum of the three internal angles of a triangle equals 180°. The three types of triangles, depending on the length of their sides, are equilateral, isosceles, and scalene triangles. The right-angle triangle is categorized by an interior angle.
Equilateral Triangle
The equilateral triangle has all three sides of equal length. It also has all the internal angles equal to 60°; hence it is a regular polygon.
If g is the length of an equilateral triangle’s side, the area of the triangle can be found by using the formula:
\[ \text{Area} = \frac{ \sqrt{3} }{4} {\text{g}}^2 \]
The perimeter of an equilateral triangle is:
Perimeter = 3g
Isosceles Triangle
A triangle with two sides equal and one side unequal is known as an isosceles triangle. If c is the length of one side of the two equal sides and f is the third side’s length, the perimeter of the isosceles triangle is given as:
Perimeter = (2c) + f
The unequal or third side is known as the base “b” of the isosceles triangle. The height “h” is the vertical line from the apex to the triangle’s base. An isosceles triangle’s area is given as:
Area = (1/2).b.h
Scalene Triangle
A scalene triangle is an irregular polygon having all three sides of unequal length. If p, q, and r are the length of three sides, the perimeter of a scalene triangle is given as:
Perimeter = p + q + r
A scalene triangle’s area is the same as that of the isosceles triangle.
Right-Angle Triangle
A right-angle triangle has a right(90°) angle. The three sides of the right-angle triangle are the hypotenuse, base, and perpendicular. The hypotenuse “h” is the longest side, the base “b” is the side adjacent to the hypotenuse, and the perpendicular “p” is the side opposite to the hypotenuse.
The Pythagoras theorem relates the length of three sides of the right-angle triangle as:
$h^2$ = $p^2$ + $b^2$
The perimeter of the right-angle triangle is:
Perimeter = h + p + b
If θ is an acute angle between the hypotenuse and the base, then the three sides are related to the trigonometric functions as:
sin θ = p/h
cos θ = b/h
tan θ = p/b
Figure 2 shows the isosceles, scalene, and right-angle triangles.
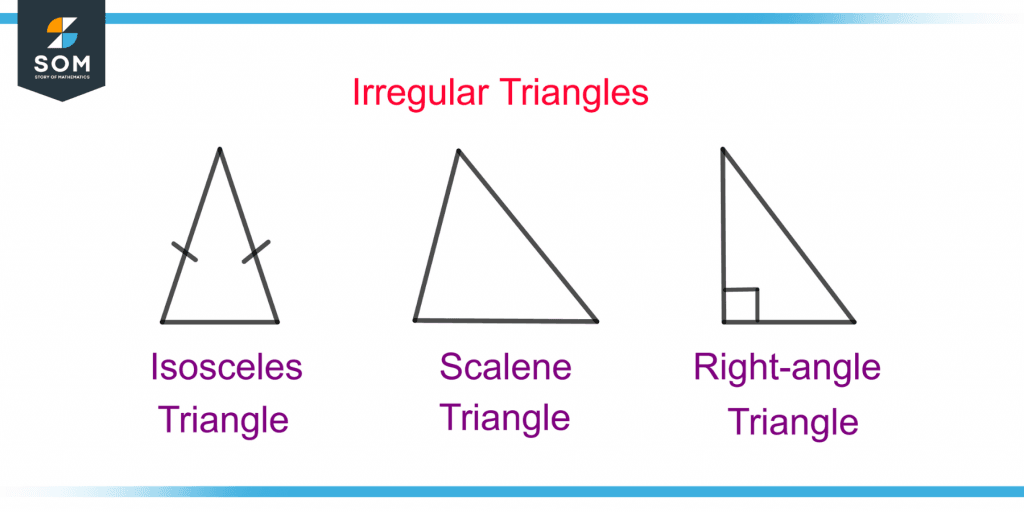
Figure 2 – Demonstration of Isosceles, Scalene, and Right-angle Triangles
Quadrilaterals
Quadrilaterals are four-sided polygons. They can be classified into different types by varying the side lengths or the internal angles as given below:
Square
A square has four equal sides. Each internal angle measures 90°, with the sum of all four internal angles equal to 360°. If e is the length of a side of a square, its perimeter is given as:
Perimeter = 4e
The formula for a square’s area is:
Area = $e^2$
Rectangle
A rectangle is an irregular quadrilateral with two opposite sides of equal length and all internal angles equal to 90°. If the length of the longer side is L and that of the shorter side is W, the perimeter of a rectangle is given by:
Perimeter = 2(L + W)
A rectangle’s area with length L and width W is given by:
Area = L.W
Rhombus
A rhombus has four equal sides, hence is also known as an equilateral quadrilateral. The two opposite angles of a rhombus are equal. If a is the length of a side of a rhombus, its perimeter is:
Perimeter = 4a
The area of a rhombus is half times the product of the lengths of its two diagonals.
Parallelogram
A parallelogram has opposite sides parallel to each other. The parallel sides are equal in length, and the opposite angles are also equal in measure. The square, rectangle, and rhombus can also be considered parallelograms.
A parallelogram’s area with base B and vertical height H is given as:
Area = B.H
The perimeter of the parallelogram is:
Perimeter = 2(r + s)
Where r is the length of the longer side and s is the shorter side’s length.
Trapezoid
A trapezoid has only two sides parallel to each other. These parallel sides are known as the bases of the trapezoid. If u and v are the length of the two bases and h is the vertical height between the two bases, the area of a trapezoid is:
Area = [(u + v).h]/2
A trapezoid’s perimeter is the sum of the length of its four sides.
Kite
A kite has two adjacent sides pairs of equal length. The two angles where the unequal sides meet are equal. A kite’s two diagonals intersect each other at a 90° angle.
The area of a kite is half times the product of the length of its two diagonals. If r is the length of the shorter side and s is the length of the longer side, the perimeter of a kite is:
Perimeter = 2(r + s)
Figure 3 shows different types of quadrilaterals.
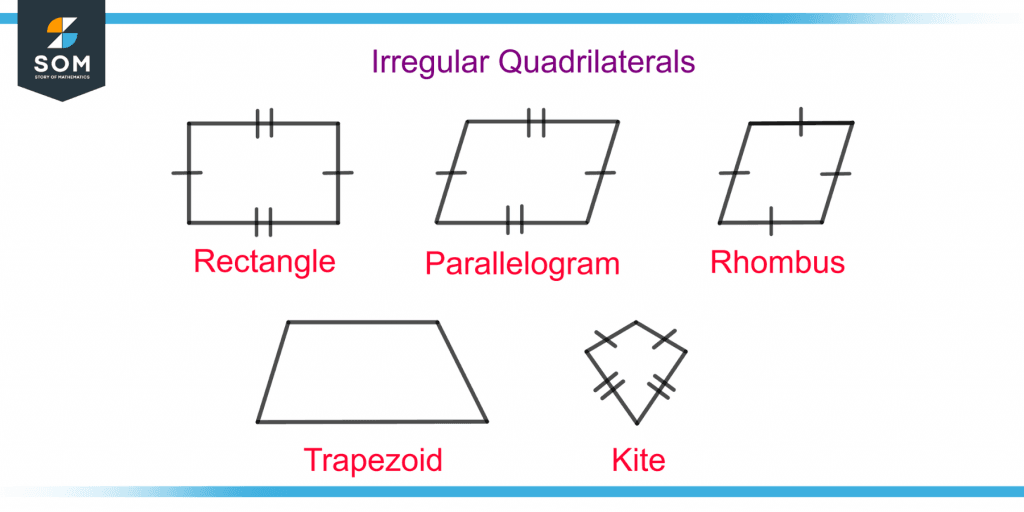
Figure 3 – Different Types of Four-sided Polygons(Quadrilaterals)
Pentagon
“Penta” means five, so a pentagon is a five-sided polygon with five angles. The sum of the internal angles of a pentagon is 540°.
Hexagon
A hexagon has six sides and six internal angles. Each angle in a regular hexagon measures 120°, with a sum of 720° of all the internal angles.
Heptagon
A heptagon is a seven-sided polygon with the sum of the seven internal angles equal to 900°. An internal angle measures 128.57° in a regular heptagon.
Octagon
An octagon has eight sides and eight internal angles. Each internal angle measures 135° in a regular octagon. The sum of the eight internal angles of an octagon is 1080°.
Nonagon
A nonagon is a nine-sided polygon with nine internal angles that sum to 1260°. A regular nonagon has nine equal sides and angles, with each internal angle equal to 140°.
Decagon
“Deca” means ten, so a decagon has ten sides and ten vertices. A regular decagon has all the sides of equal length, with each interior angle equal to 144°. The sum of the internal angles of a decagon equals 1440°.
Figure 4 shows all types of polygons(regular) with sides of equal length.
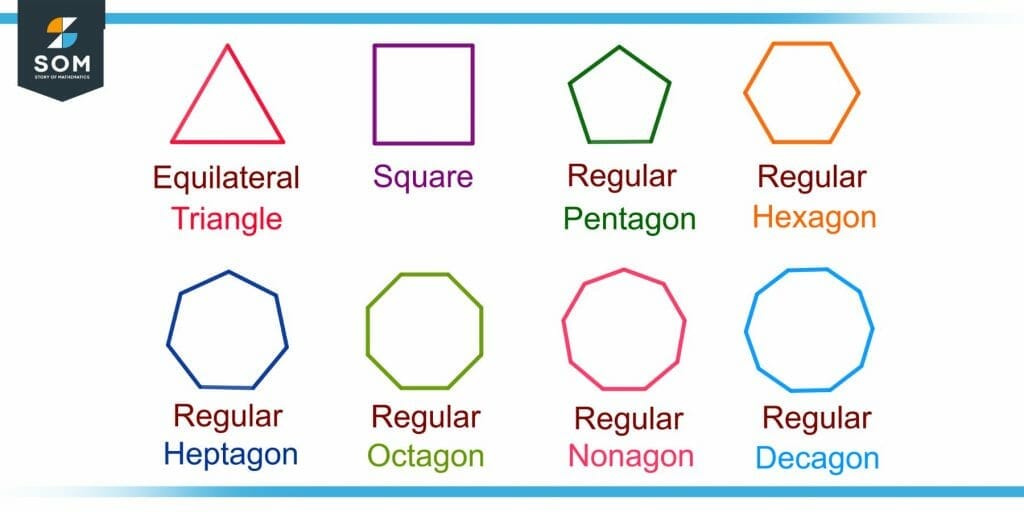
Figure 4 – Different Types of Polygons with Sides of Equal Length
Number of Diagonals of an m-sided Polygon
A line segment formed by joining two non-adjacent vertices in a polygon is known as a diagonal. Non-adjacent vertices are not on the same side of a polygon. The number of diagonals of an m-sided polygon can be found by using the formula:
Number of Diagonals = m(m – 3)/2
For example, the total number of diagonals that can be drawn in a heptagon(m=7) are:
Number of Diagonals in a Heptagon = 7(7-3)/2 = 14
Figure 5 shows all the possible diagonals that can be drawn in a four, five, six, and seven-sided polygon.
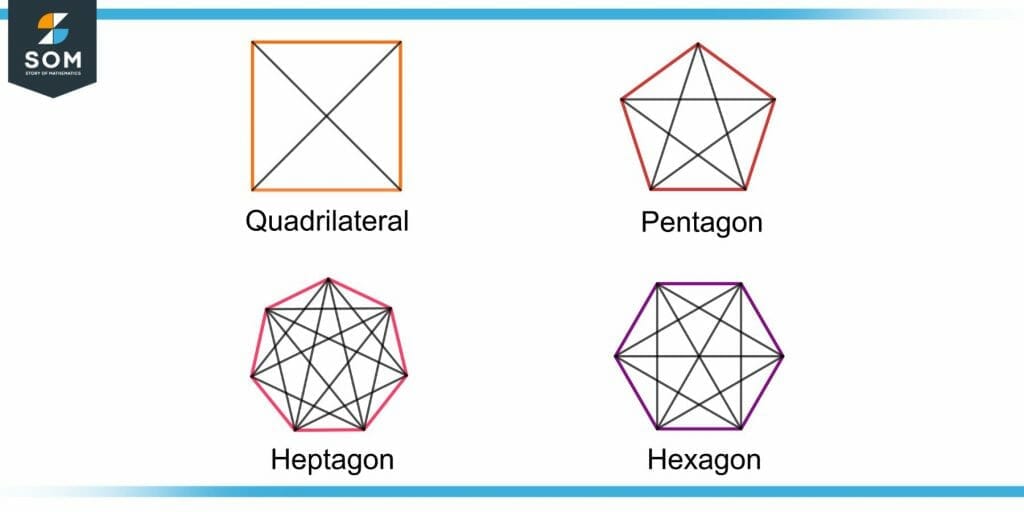
Figure 5 – Number of Diagonals in a Four, Five, Six, and Seven Sided Polygon
Polyhedrons
A polyhedron is a three-dimensional object with its faces as its sides. The edges of a polyhedron are the line segments joining two sides. For example, a cube is a regular polyhedron with a square as a polygonal face.
An Example of Using Side Lengths to Find the Area and Perimeter
A parallelogram has a base length of 5 cm and a height of 7 cm. The length of the other side is 3 cm. Calculate the area and perimeter of a parallelogram. Also, calculate the number of diagonals of a parallelogram.
Solution
The area of a parallelogram is given by:
Area = B.H
Here,
B = 5 cm, H = 7 cm
Putting the values in the above equation gives:
Area = (5)(7) = 35 cm$^2$
The perimeter of a parallelogram is given by:
Perimeter = 2(r + s)
As the base is a side of the parallelogram, so
r = 5 cm
And the length of the other side is given as follows:
s = 3 cm
Putting the values gives the perimeter of the parallelogram as:
Perimeter = 2(5 + 3) = 2(8) = 16 cm
The number of diagonals of a parallelogram can be found by using the formula:
Number of Diagonals = m(m-3)/2
As a parallelogram is a quadrilateral(four-sided), so
m = 4
Putting the value of m gives:
Number of Diagonals = 4(4-3)/2 = 4/2 = 2
All the images are created using GeoGebra.
