JUMP TO TOPIC
Signed Number|Definition & Meaning
Definition
If a number is written along with its sign (+ or -), it is a signed number. For example, +90 and -17 are both signed numbers. Negative numbers appear on the left of 0 on the real line, while positive numbers appear on its right. We only need to use signed numbers if we are dealing with negative numbers in our problems since unsigned numbers are assumed to be positive.
A real number, often known as a number that does not contain any imaginary components, can either be positive (more than zero) or negative (less than zero), or it can be equal to zero. Real numbers, which do not include zero, are referred to as signed numbers. As an illustration, the numbers -3, -1.5, 2, 2.56, and 100 are all examples of signed numbers.

Figure 1 – Signed numbers representation
In the fields of mathematics and science, signed numbers play a significant role because the sign can signify either gain or loss, as well as the direction of motion or rotation.
In mathematical notation, a negative number is denoted by putting a minus sign right in front of the digit portion of the number, whereas positive numbers do not have a sign placed in front of them. The number “-10” is considered negative, while the number “10” is considered positive.
The magnitude of the number, which is the number itself without the sign, and the sign itself determines the value of a signed number. The magnitude of a number is the distance from zero that it represents. A number is positive if its magnitude is greater than zero, while a number is said to be negative if its magnitude is smaller than zero.
For instance, both -5 and 5 have magnitudes of 5, meaning they are equally far away from zero (five units). When expressed as a number, a negative five is five less than zero, and a positive five is five more than zero.
Positive Sign
The symbol for addition is the plus sign (+), which is also known as the positive sign. Any integer other than zero without a negative sign to its left is considered to be positive by default since the positive sign is assumed to be present in mathematics. As an illustration, the numbers 1.4, 45, and 700 are all considered positive, although 0 and -3 are not.
Mathematically speaking, when a plus sign is utilized as a positive sign rather than an addition sign, it often draws attention to the direction that is connected with being positive.
For instance, a record that is turning at a rate of +30 degrees per second is moving in an anticlockwise direction because the positive direction of rotation in both mathematics and physics is defined as being anticlockwise.
In addition, a bird traveling in a horizontal plane with a velocity of +2 miles per hour moves in an easterly direction. This is because the positive horizontal direction is rightward, much like a graph.
Negative Sign
The symbol for subtraction is the same as the negative sign(-), which is a dash. The negative sign, in contrast to the positive sign, does not appear implicitly; rather, a negative number is the only thing that can have a negative sign in front of it. For instance, -1.4 and -700 are both examples of negative numbers.
In mathematics, using a negative sign indicates that the corresponding number is greater than zero. In addition to that, it can be utilized to change the sign of a number or variable. (-(-2)), for instance, equals 2 because the outer negative sign reverses the meaning of the inner one.
In addition, the -x operator will reverse the sign of x even if the original sign of x is unknown.
Additive Inverse
A signed number’s additive inverse or opposite has the same magnitude as the original number but a different sign. As an illustration, -2 and 2 are examples of additive inverses. Because additive inverses always cancel each other out, the sum of a number and its additive inverse is always equal to zero.
To find the additive inverse of a signed integer, you need just to keep the digit(s) and reverse the sign. If the original number was negative, you need to remove the negative sign from it, and if the original number was positive, you need to write a negative sign in front of it.
Number Line
Because vector quantities include both magnitude and direction, it is vital to utilize signed numbers in arithmetic and science. For example, 20 meters per second south or 30 degrees per second clockwise are both examples of vector values. Only the magnitude is indicated by the digits, while the sign specifies which way the value should be read.
A number line, which functions similarly to the x-axis of a coordinate plane, can be of assistance for solving problems involving positive and negative signed numbers.
On a number line, the negative values are located to the left of 0, while the positive numbers are located to the right of 0. The placement of large negative numbers relative to smaller negative numbers is to the left, and the placement of large positive numbers relative to smaller positive numbers is to the right.
When attempting to depict a signed number using a number line, first determine the magnitude of the number, then move the appropriate number of places away from zero on the number line (see Figure 2). The direction to move in for positive numbers is to the right, and the direction to travel in for negative numbers is to the left.
As an illustration, in Figure 2, the red dot stands for the value -2, whereas the blue dot denotes the value 3.
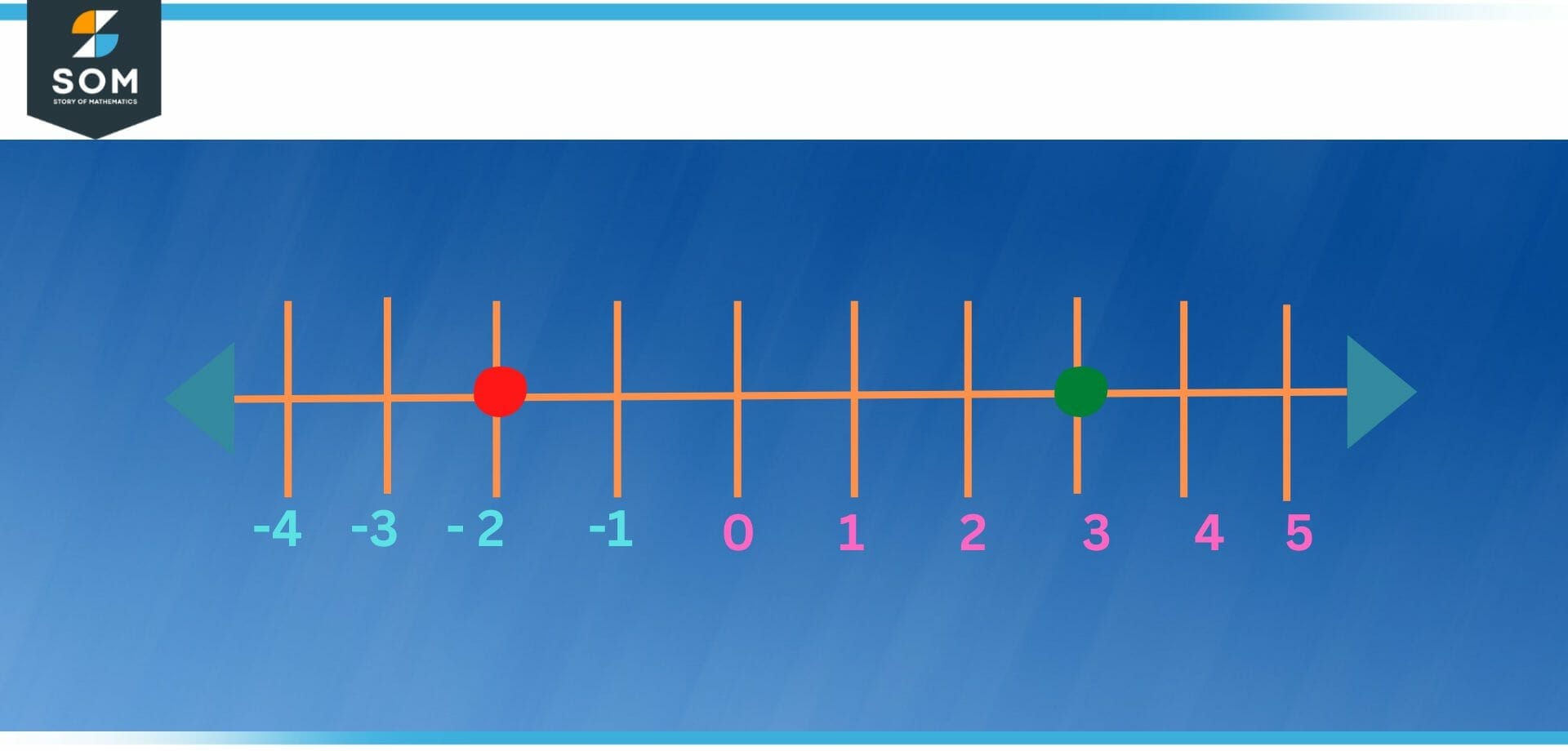
Figure 2 – Negative two and positive 3 on a number line.
Addition of Signed Numbers
A mathematical operation known as “the addition of signed numbers” combines two numbers that can have opposite signs or the same signs in order to arrive at a final total. The final product of the addition could be a number with a positive or negative sign, depending on the signs of the numbers that were added together.
There are two principles that must be followed when adding signed numbers together:
If the signs of the numbers are the same, add the numbers and give the result the same sign as the numbers that were being added. If the signs of the numbers are different, give the result the opposite sign. For instance:
(+6) + (+2) = (+8)
(-6) + (-2) = (-8)
If the signs of the numbers are not the same, subtract the absolute values of the numbers and then give the result the same sign as the number that has the greater absolute value. For instance:
(+4) + (-1) = (+3)
(-4) +(+1) = (-3)
It is essential to keep in mind that the procedures for adding signed numbers are predicated on the idea of absolute value. Absolute value refers to the positive worth that a number possesses regardless of the sign that it carries.
Subtraction of Signed Numbers
Calculating the difference between two integers that may have opposite signs or the same signs is the objective of the mathematical operation known as the subtraction of signed numbers.
There are two principles to follow when subtracting signed integers from unsigned numbers:
- Start by subtracting the absolute values of each of the numbers, and then give the result the same sign as the number that has the highest absolute value.
- If the signs of the numbers are not the same, then add the absolute values of the numbers, and give the resulting number the same sign as the number that has the positive sign.
For instance:
(8) – (+3) = (5)
(-8) – (+3) = (-11)
(-8) – (-3) = (-5)
Remember that the rules for subtracting signed numbers are derived from the rules for adding signed numbers as well as the idea of absolute value. This is an essential fact to keep in mind.
Signed Numbers’ Comparison
Signed numbers are able to be ranked in either the most significant to the least significant or vice versa. The following are the actions that need to be taken when comparing signed numbers on a number line:
- On a number line, locate each of the numbers that have been signed. On a number line, for instance, the numbers -2.5, -1, 0.5, 2, and 3 are presented from left to right in Figure 3. Remember that positive numbers are located to the right of zero, whereas negative numbers are located to the left of zero.
- To determine the order of the numbers from lowest to highest, read the number line from left to right. Another option is to read the number line from right to left in order to arrange the numbers in descending order from highest to lowest.
- For example, the following is a list of the numbers seen in Figure 3 in ascending order: -2.5, -1, 0.5, 2, 3, and so on. The following is a list of the numbers in their decreasing order: 3, 2, 0.5, -1, and -2.5.
- If you don’t have a number line, you can rate the numbers from lowest to highest by listing them in this order: First come the negative numbers that are approaching zero (i.e., larger negative numbers than smaller negative numbers), then 0 comes next, and finally the positive numbers come after that.
- For instance, the sequence in which the numbers 9, 0, -1, and 2 are ordered is as follows: -10, -1, 0, and 2. To determine the totals, list them in descending order from the highest to the lowest.
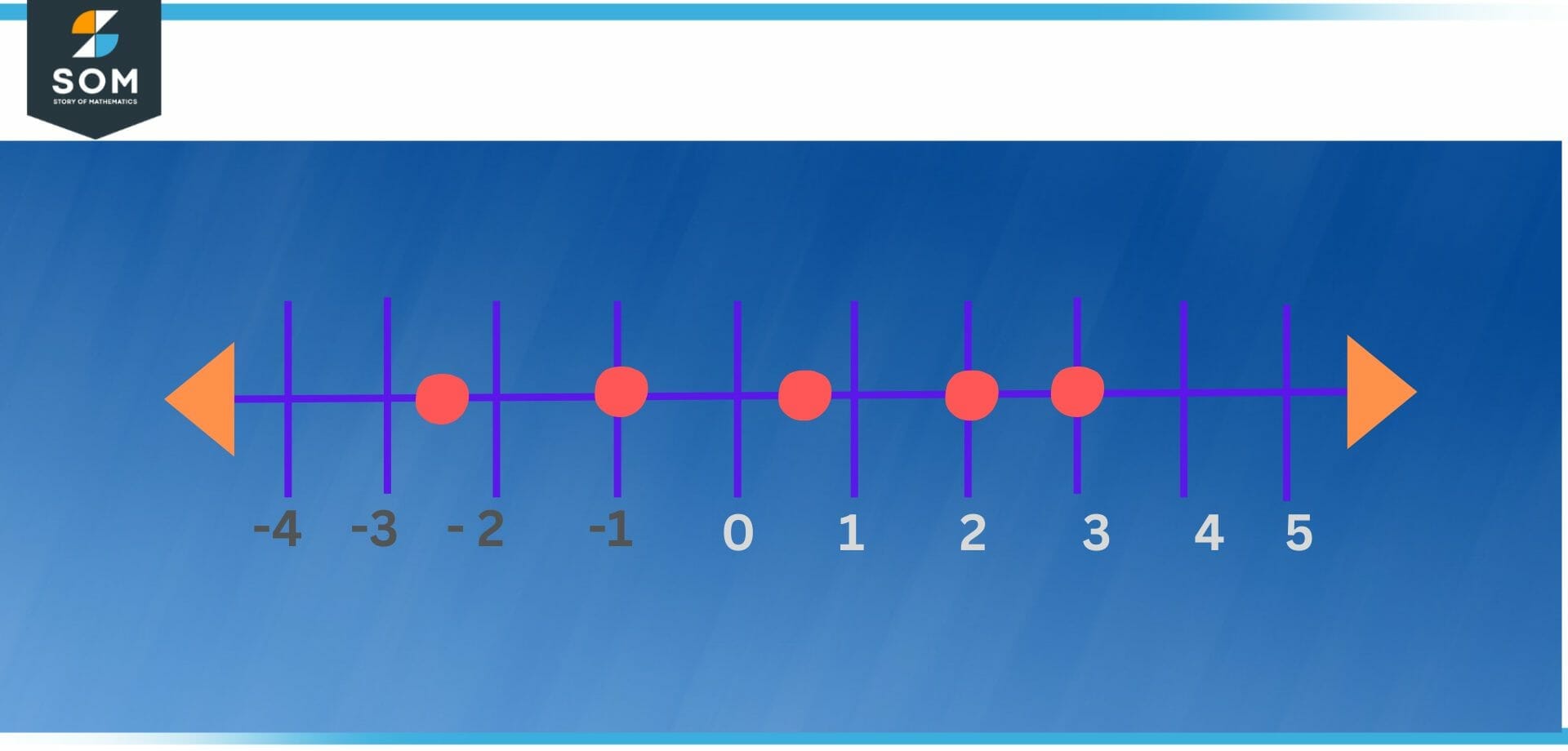
Figure 3 – Locate each of the signed numbers from left to right on a number line.
Example
Find the difference when we subtract a greater number from a smaller number:
4 − 9
What will be the sign of the answer that has been found?
Solution
To assert that we cannot get 9 from 4 would not be an incorrect statement. Naturally, we are able to deduct 4 from 9, and that is exactly what we do; however, when we report the solution, we use a minus sign.
4 − 9 = −5
Even when we are doing algebra, all we can do is simple arithmetic. But after that, we have to decide which sign to use.
It is possible to refer to this principle as the first rule of signed numbers.
All images/mathematical drawings were created with GeoGebra.
