Significant Digits|Definition & Meaning

The fraction of a number that can be confidently measured. All the digits from the first nonzero digit to the right of the decimal point are considered significant. If there are no nonzero digits before the decimal point, the first digit to the right of the decimal point is also considered significant.

What Are Significant Digits?

The precision of every measurement has a certain upper bound somewhere. The accuracy of your results is entirely dependent on the precision of the measuring tool you employ. If you multiply or divide two or more numbers, the result will have as many significant digits as the smallest of the numbers you multiplied or divided. 

When performing an arithmetic operation, the numbers are determined by the least significant figure among the amounts being added or subtracted. As an illustration, the correct notation for the sum of 10.234 + 5.2 + 100.3234 is 115.7574, however, this should be rounded down to 115.8 (with rounding) because the value of 5.2 is only accurate to within +/-0.1.

Figure 1 – Significant Figures of Whole Numbers

The above figure shows the significant digits of some random numbers.

The Rule for Significant Digits

Here are several criteria for determining the number of significant digits in a given number.

Significant Digits With Non-zero Digits

Numbers with non-zero digits always have meaning. Therefore, 11 has only two significant numbers, while 11.4 has three.

Significant Digits With Leading Zero

When zeroes are involved, things get trickier. The leading zeroes in numbers are ignored, so 0.086 contains just two meaningful digits.

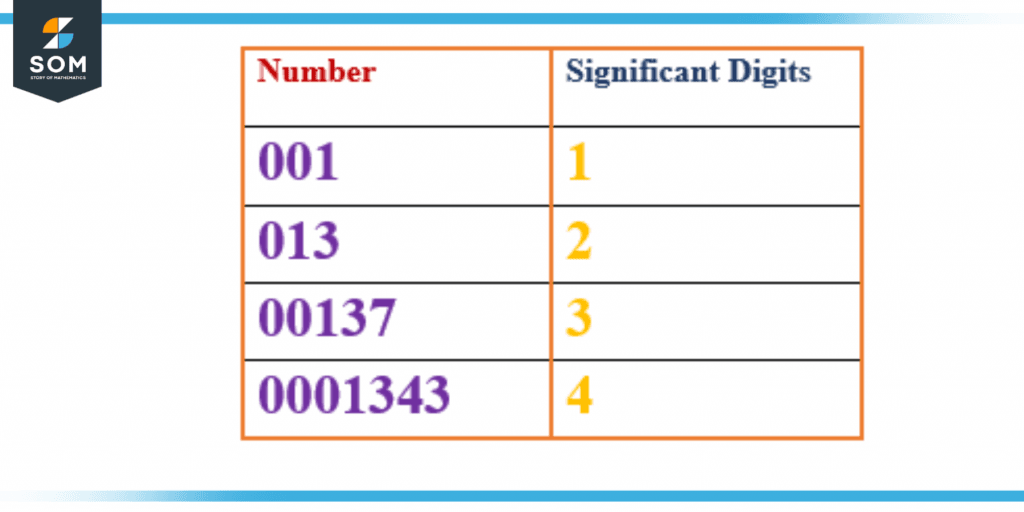
Figure 2 – Significant Digits when Leading Zeros

In the above figure, it can be clearly seen that the leading zero will not be counted in significant digits.

Significant Digits With Zero Between Numbers

Zeroes put between other non-zero numerals are always counted. There are four significant digits in the number 4004 because zeros are in between non-zero numbers.

Significant Digits Involving Decimals

Significant digits include the digits before and after a decimal point; for example, 4.90 contains three significant digits because the third and fourth digits are zeroes.

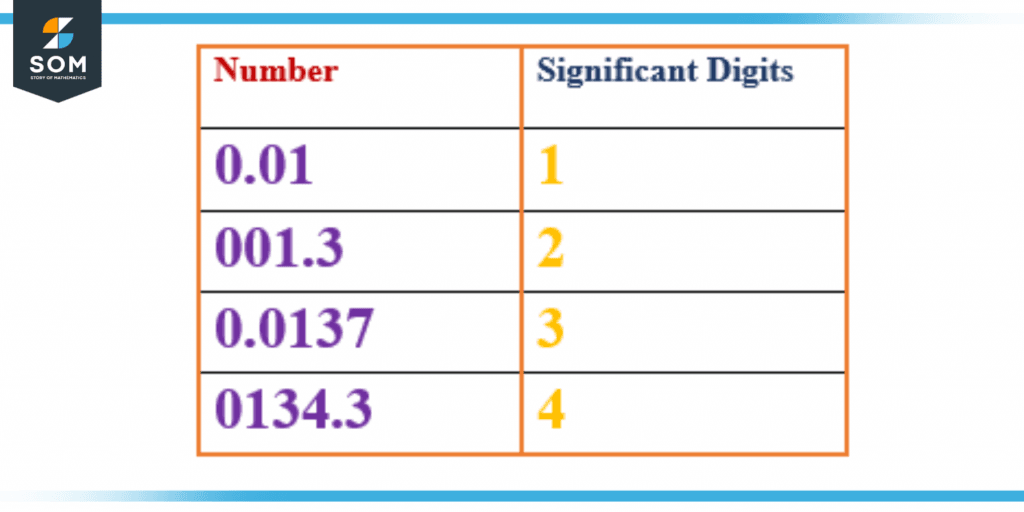
Figure 3 – Significant Digits of Decimals

The above figure shows significant digits of the decimals involving leading zero.

Significant Digits With Zeros at the End

The only time the digits “0” just at the end of the number are meaningful is when they’re tried, followed by decimals. If you don’t know the context, you can’t judge their significance. With number 2200, for instance, it is unclear whether or not the leading zeroes are meaningful. 2200 may have three or four significant digits, with two being the minimum.

Putting significant zeroes after a decimal point in scientific notation is a good way to eliminate guesswork.

It takes four significant digits to represent the number 2.200 x 10³. Three meaningful digits are present in the value 2.20 x 10³.

Having two significant digits, the number 2.2 x 10³ is quite large.

Significant Digits Involving Addition and Subtraction

When performing calculations involving addition and subtraction, it is best practice to reduce the final answer down to the fewest possible decimal places in the measures that are being added or subtracted. Note: When adding or subtracting full numbers, you should round the results to the same significant number of numbers as the measurement with the least amount of precision.

Significant Digits Involving Multiplication and Division

When performing operations such as multiplying, dividing, complex numbers, etc., the answer should have as many significant digits as the smallest of the numbers used in the computation.

When dealing with several operations, it is necessary to carry out the full calculation using all of the numbers. The next step is to establish the number of key digits or decimals placed at each stage (while adhering to the right order of operations). It is beneficial to highlight the “additional” decimal places or significant digits that are being carried over to the subsequent step.

The final answer should be rounded to the same significant number of digits or decimals placed as the component of the computation that requires the least amount of precision.

Rounding the Significant Digits

For rounding a number to the desired number of significant digits, one or even more digits from the right side of the number are dropped. The final digit that is held should be kept the same whenever the very first digit in the leftmost position is less than 5. The value of the left digit is rounded up whenever the value of the right digit is larger than 5.

The number that is held is rounded either up or down depending on whether or not it is an even number when the digit that is left is exactly 5. When there is still more than one digit, rounding should have been done as a whole rather than one digit at a time when there is more than one digit left.

When rounding off the significant numbers, there are two principles to follow:

• The first thing that we need to do is choose the most significant digit to which we should round the number. If the number that comes after the digit that is used to round off is fewer than 5, then we will need to eliminate all of the numbers that are on the right side of the equation.
• However, if the digit that is directly adjacent to the digit that is being rounded off is more than 5, then we need to add one to the digit that is being rounded off and disregard the other numbers that are on the right side.

An Example of Significant Digits

To the fifth significant digit, rewrite this number 13.372167. 

Solution

When rounded down to 5 significant digits, the number 13.372167 becomes 13.372.

As a result, the correct response is 13.372.

All the figures above are created on GeoGebra.

Signed Number Definition < Glossary Index > Similar Definition