Similar|Definition & Meaning

Two figures are referred to as similar and analogous if they contain the same shape. The concept of being similar has been elaborated in Figure 1 below:

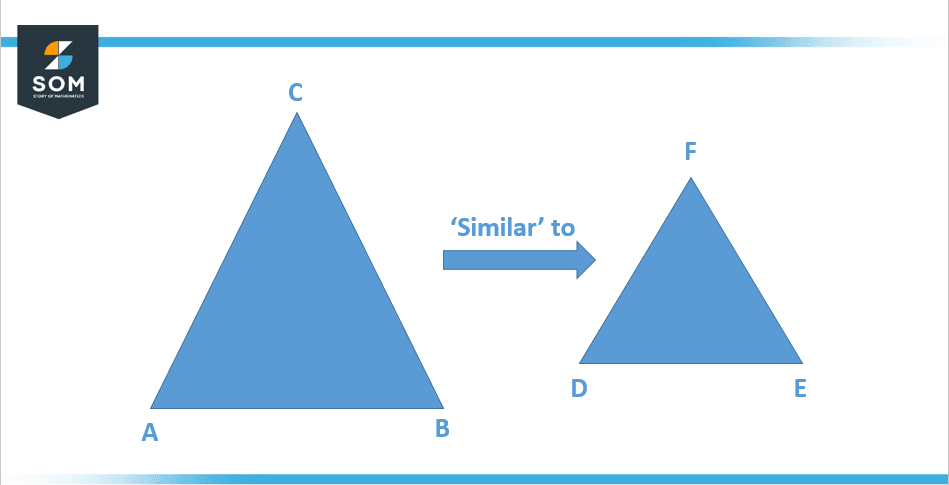
Figure 1: Concept of similarity in shapes

In more formal terms, two figures are said to be similar if their respective angles are congruent and their connected side length ratios are equal. The scale factor is the name given to this common ratio. The symbol ‘∼’ is used to denote similarity, but similarly does not mean the same in size.

When all comparable angles are identical, and all lengths are enlarged (or shrunk) by the same ratio, known as the magnification ratio, two figures are said to be similar. A transformation that takes figures to similar figures is called a similarity. 

Alternatively, when all comparable angles are identified and described in the same rotational sense, two figures are said to be directly similar. A∼B is a symbol of this partnership. (The symbol ‘∼’ is also used to denote the terms “is asymptotic to” and “is of the same order of magnitude as”).

However, when all related angles are equal and described in the opposite rotational meaning, two figures are said to be inversely similar. This requirement is pictured in Figure 2 below:

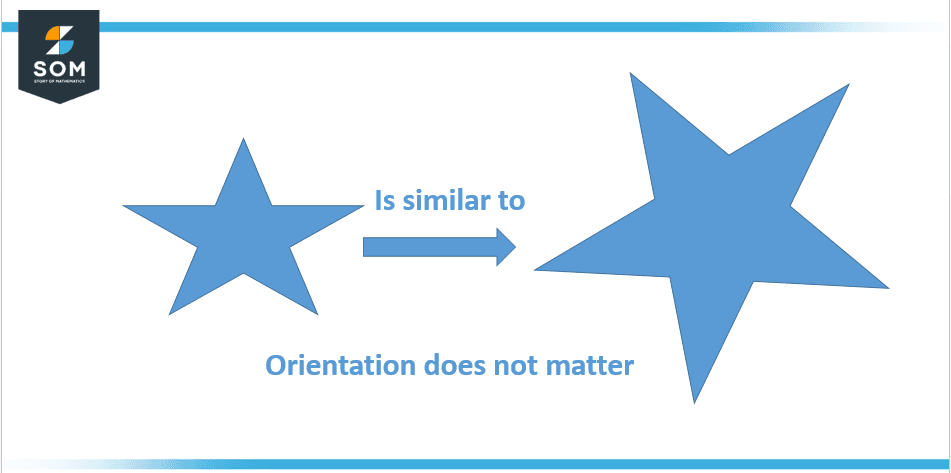
Figure 2: Impact of orientation on similarity

Similar figures are two objects that share the same shape but vary in size.

To put it another way, two numbers are considered to be comparable when they share a number of traits but aren’t necessarily the same. For instance, despite appearing to be the same size, the sun, and moon are actually different sizes.

However, because both of our figures are circular in shape, they are similar figures. This phenomenon is seen as a resemblance property while taking shape and distance into consideration. By describing similar figures, their use in geometry, and solving a few cases, let’s learn more about this attractive idea.

Similarity in Shapes

When two or more objects or figures have the same or equal shape, this is referred to as similarity or similar figures. These figures always superimpose one another regardless of how they are magnified or diminished.

When two shapes, such as triangles, polygons, or quadrilaterals, have the same dimension or common ratio but different sizes or lengths, they are referred to as similar figures in geometry. As an illustration, two circles (of any radii) can have the same shape but different sizes due to their similarity. Similar does not, however, imply the same size.

Similarity of Triangles

If the sides are in the same ratio or proportion and the angles are equal (corresponding angles), two triangles will be similar (corresponding sides).

Similar triangles may have varying individual side lengths, but they must have equal angles and the same scale factor or matching ratio of the side lengths. If two triangles are similar to one another, then:

• All corresponding angle pairs of triangles are equal.
• All corresponding sides of triangles are proportional.

Similarity of Polygons

Polygons that share the same shape but differ in size are called similar polygons. Similar polygons would have specific, consistent ratios. The respective sides are proportionate, yet the corresponding angles are congruent.

Straight lines make up the two-dimensional shapes known as polygons. Because all of the lines are connected, they are considered to have a closed shape. Two essential characteristics of comparable polygons are:

• Angles on either side are identical or congruent (the angles are the same from the inside and outside).
• All sides have the same ratio of the corresponding sides. The perimeters are altered as a result.

Similar polygons have been shown in Figure 3 below:

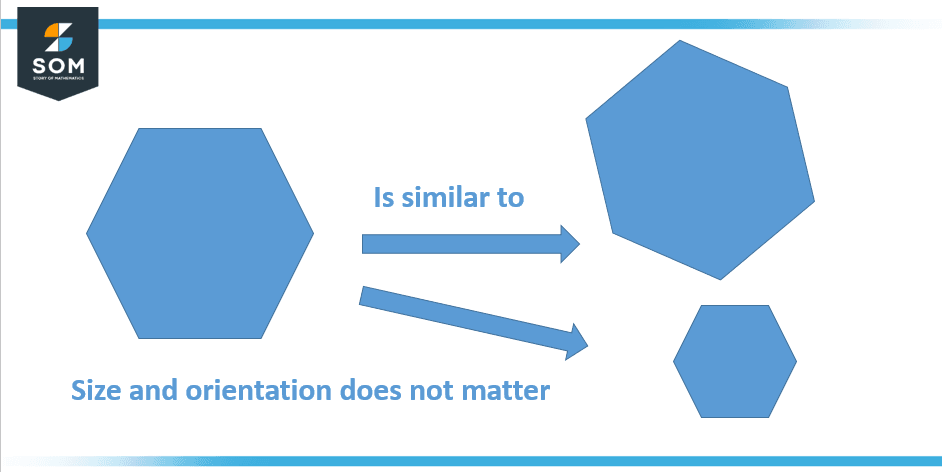
Figure 3: Illustration of similarity in polygons

Quadrilaterals Polygons

Four-sided polygons are referred to as quadrilaterals. A quadrilateral’s interior angles add up to 360 degrees. When two quadrilaterals’ two adjacent sides have equal ratios, and their three corresponding angles are the same (the fourth angle automatically becomes identical because the sum of internal angle is equal to 360 degrees), then the two quadrilaterals are similar.

How Similarity Is Used in Real-World Situations

Despite having varying sizes, comparable figures all share the same shape.

Contrary to congruent figures, which are exact duplicates of one another, similar figures can be described as having a proportional relationship to each other.

Real-world measurements of angles, rivers, and building heights and distances are all done using the similarity principle. Below are a few examples of the applications of similarity.

• The similarity is widely used in architecture.
• Solving problems involves height and distance.
• Solving mathematical problems involving triangles.

The concept of similarity can aid in the simplification of difficult issues that must be resolved in practical scenarios. For instance, you don’t have to climb all the way to the top of a structure to determine its height. Simply measuring its shadow and comparing it to the shadow of an object with a comparable structure can do the same thing.

The user can determine the river’s breadth by using the similarity of the angle’s principle. Using that, we can guess the length of a ship’s mast when its shadow forms an angle with the riverbank. It enables estimation of the bridge’s height needed to address the transportation issue.

The concept of similarity is used while creating models for prospective buildings in a few professions, including architecture, computer-aided modeling, and infrastructure development.

Scaling the model up to a complete structure becomes an easy and seamless procedure when it is accurate and results from in-depth knowledge of similarity. As a result, one of the primary applications of the concept of similarity that receives a lot of support is in the development of model visualization utilizing synonymy and difference.

Difference Between Similarity and Congruence

• In geometry, the similarity and congruence of the terms are connected to shape and size. In contrast to similar figures, which have the same shape but a different size, congruence refers to the same structure, size, and shape.
• Figures are said to be congruent if they are the same size and shape. Similar or similar figures are those that have the same shape but different sizes.
• Congruent figures are superimposed and have the same dimensions. Although similar figures are identical, they cannot be superimposed on each other.
• Congruence follows theorems of similarity. Similarity does not follow any theorems.
• Congruence can be described as coincidental and superimposed. Figures that are similar in nature can be made congruent after some manipulations on one of them.

Important Notes

• The third angle of a triangle will always be equal if the first two angles are.
• A triangle is always divided into two similar triangles by its angle bisector (Theorem of the Angle Bisector).
• The ratio of the dimensions or areas of two similar triangles will be equal if their sides are in the same ratio.

Examples of Similar Shapes

State at least three figures or shapes that can be similar.

Solution

Following are three examples of similar figures:

• Pair of equilateral triangles.
• Pair of squares.
• Pair of circles.

All images/mathematical drawings were created with GeoGebra.

Significant Digits Definition < Glossary Index > Simple Interest Definition