Simplest Form (Algebra)|Definition & Meaning

What Is Simplest Form?

Anything that has been reduced to the minimum possible level or that requires not much effort to reduce it further is known as the simplest form. In mathematical algebra, the simplest form is the least attainable fraction of a number or a linear equation. 

If we talk about fractions, the numerator and the denominator have to be simplified up till the last bit in order to say that we have achieved the simplest form.

For instance, we have a fraction, 1/2, which is in its simplest possible formation and can not be further reduced as a whole number fraction.

Figure 1 – A simplified whole number fraction

What Are Algebraic Expressions?

The concept of algebraic expressions is the use of words or alphanumeric characters to present data without providing their accurate value. We were taught how to represent an unspecified number using symbols like x, y, and z in the fundamentals of mathematics. Here, we refer to such characters as variables.

A calculation may have both constants and variables. Coefficients are these number that comes in front of a variable and is transformed by it.

Algebraic expressions are also composed of arithmetic operations such as addition, subtraction, etc.

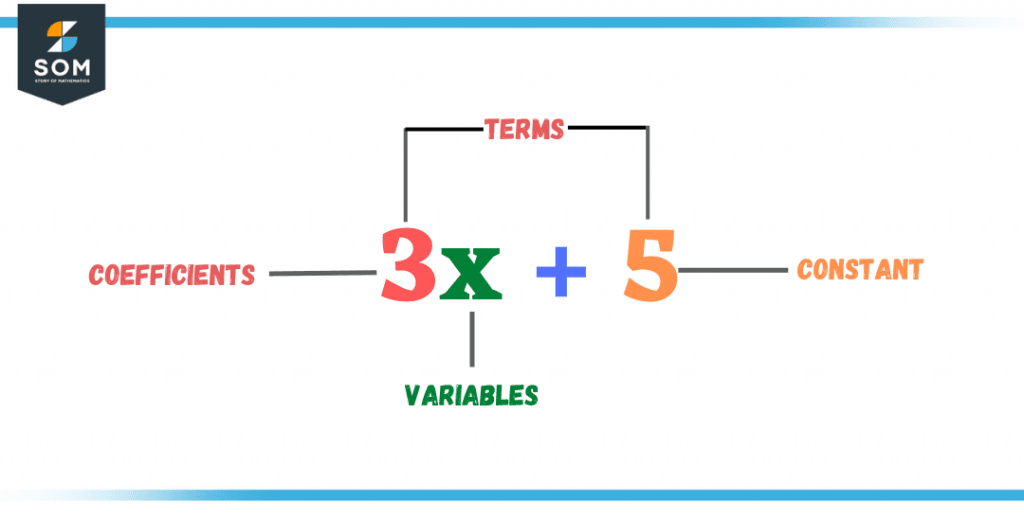
Figure 2 – An algebraic expression of the simplest form

An expression consists of three elements, namely, coefficients, variables, and constants. The elements separated by any arithmetic symbol are known as a term. So in the above expression,

• x represents a variable whose actual value is not known and can contain any virtual value.
• The number 5 next to the variable x is known as a coefficient. Coefficients are usually constant values and are used with variables such as the above. They enhance the value of a variable by increasing it or decreasing it if they are in the denominator.
• The last element that is usually separate from the other terms is a constant, and as the name suggests, it is a well-defined numerical value. In this case, 3 is a constant.

The above expression is known as a binomial expression which means it has two (bi) elements with no similarity between them.

Type of Algebraic Expressions

The three most common types of algebraic expressions are explained below.

Monomial Algebraic Expressions

These are the most basic expressions consisting of only one element; that’s why they are known as monomial expressions. Such as 5y², 10x, etc.

Binomial Algebraic Expressions

These contain two elements, both can be variables or can contain one variable and one constant. Such as 10xy + 3, 5x² – 5y, etc.

Polynomial Algebraic Expressions

An expression containing more than two elements is known as a polynomial expression. All the terms in this expression are different from one another. Such as 2x + 7y + 4z + 6, etc.

What Is Simplifying?

A straightforward meaning of simplifying is to make things easy. In mathematical terms, simplifying is downsizing the equation, expressions, fractions, or any problem to the least minimum form. The benefit of simplifying expressions can help in calculations and solving a particular problem.

Most mathematical expressions cause a nightmare for the students, so the idea of simplifying is to lower their pain and guide the subject as efficiently as it can; therefore, simplifying algebraic expressions can assist us in making mathematical calculations easier.

The steps to follow for simplifying any expression are quite easy to comprehend; you will start by removing the symbols of similar groups or parentheses and brackets in simple terms and then combining the similar terms having the same exponent or maybe the same variables. It is an instrumental process of converting a complex form into a simpler one.

Steps for Finding the Simplest Form

The steps for finding the simplest form are as very simple as the name suggests.

For an Algebraic Fraction

• The first step is to find factors that are similar in numerical values or are coefficients of similar variables. Also, look for exponents, and combine the monomials having similar exponents.
• The next step is to find a fraction in which one of the factors is a prime factor. Now a prime number is such a number that is divisible only by itself, such that it only generates two factors, one and itself.
• The last step is to multiply and divide by the same number so that its fraction is 1. Simply multiplying the fraction with a number will obviously make it larger instead of reducing it, so it is recommended to multiply and divide by the same number, such as 2/2, 5/5, etc.

For an Algebraic Expression

Merge Similar Terms

Identifying similar terms is pretty straightforward; you just have to look for similar variables or variables having the same exponents, such as:

 = 10x + 5x

 = 15x

If the terms are not similar to any of the available terms, then that means the expression is already simplified to the least minimum, such as:

 = 6x + 2x²

The above expression does have the same variable used, but the powers are different, which makes it unlike terms, and thus they cannot be merged into a more simplified form.

Use of Distributive Property

When there are parentheses or square brackets in an expression, the best approach is to eliminate them first before moving forward. Such a simple expression like:

 = 4(5x + 9) + 3x

can be simplified if the parenthesis is removed. In this scenario, the distributive property can help us to remove the parenthesis by multiplying the number outside with the elements inside the parenthesis. Thus resulting in a long but simplified expression.

Let’s simplify the above expression by applying the property,

Figure 3 – Using distributive property to simplify an algebraic expression

Solved Example of a Simple form of Algebraic Expression

Simplify the expression given below

\[ \dfrac{(x^2 – x)(x^2 + 5x + 6)}{(2x + 6)(x^2 – 1)} \]

Solution

The first step is to figure out the factors of the numerator and denominator. The numerator can be factorized as:

x(x – 1) . (x + 3)(x + 2)

Similarly, the denominator can be written after factorizing as:

2(x + 3) . (x + 1)(x – 1)

Now simply eliminating similar terms from the fraction gives us the following:

\[ \dfrac{(x\cancel{(x – 1)}).\cancel{(x + 3)}(x + 2)}{(2\cancel{(x + 3)}).\cancel{(x – 1)}(x + 1)} \]

Now we can multiply the remaining terms of the fraction to get:

\[ \dfrac{x(x + 2)}{2(x + 1)} \]

\[ = \dfrac{x^2 + 2x}{2(x + 1)} \]

Usually, when we simplify fractions, we leave the denominator as it is, whereas the numerator gets multiplied and forms a whole expression. This practice can be helpful when you encounter a situation in which you require the least common multiple of a complex equation and have denominators with similar factors.

All images are created using GeoGebra.

Simple Interest Definition < Glossary Index > Simplest Form Fractions Definition