Simplest Form (Fractions)|Definition & Meaning

A fraction is a numerical expression representing a subset of the whole. The reduced form of a fraction is another name for its most basic form. For instance, the simplest representation of a fraction with a common component of 1 is $\frac{3}{4}$. The simplest form, however, is not $\frac{2}{4}$ since $\frac{1}{2}$ is a further simplification of $\frac{2}{4}$ that may be written. In this case, we can also claim that the fractions $\frac{1}{2}$ and $\frac{2}{4}$ are equal.

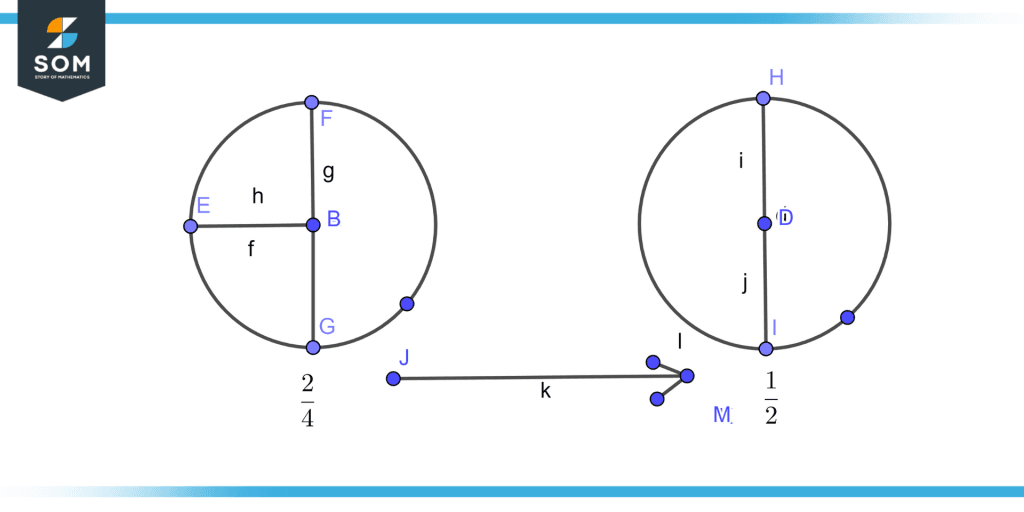
Figure 1 – The simplest form of fractions.

Figure 1 illustrates the example of the simplest form of fraction as $\frac{2}{4}$ can be equivalent or can be written in simplest form as $\frac{1}{2}$. 

Simplest Form of Fractions

When the top and bottom of a fraction are relatively prime integers, the fraction is said to be in its simplest form. In their most basic form, fractions are straightforward to locate. By dividing the numerator and denominator of a fraction by the greatest common divisor that divides them exactly, you can easily simplify the numerator and denominator of the fraction.

After division, the numerator and denominator must both still be integers. This fraction-simplifying procedure is also known as fraction reduction. The fraction $\frac{ac}{bc}$ is reduced to $\frac{a}{b}$ by removing the common component “c” from both the numerator and denominator.

To simplify a fraction, divide its top and bottom by the largest integer that divides both values equally (they must stay whole numbers).

Steps To Find the Simplest Form of a Fraction

• Find the Highest common factor (HCF) of the Numerator and Denominator of a Fraction.
• Divide the numerator and denominator by the generated HCF.
• Write the abbreviated fraction of the given fraction.

 Simplest Form of Fractions With Exponents

Fractions with exponents in the numerator and denominator can be simplified. To simplify fractions with exponents, use the exponential extension form in the numerator and denominator. Exponents are sometimes used to make numbers easier to read.

Simplest Form of Fractions With Variables

It is also possible to simplify fractions that have variables in the numerator and denominator. Use the extended form of each word in the numerator and denominator to simplify fractions with variables.

Simplest Form of Fractions With Mixed Fractions

A proper fraction and a whole are combined to form a mixed fraction. You must only simplify the fractional component of a mixed fraction in order to simplify it. To do this, factor the denominator and numerator and eliminate any shared components. The new numerator and denominator of the mixed fraction will be the outcome.

Steps to form the simplest form of fractions with Mixed Fractions

• Find the fraction’s numerator and denominator’s highest common factor (HCF).
• To obtain the simplified fraction, divide the denominator and numerator by the highest common factor (HCF).
• Together, write the simple fraction and the entire amount.

Simplest Form of Fractions With Improper Fractions

If the numerator of a fraction is higher than or equal to the denominator, the fraction is deemed as an improper fraction. Inappropriate fractions should be converted to mixed fractions for simplification. This means dividing the numerator by the denominator. It is then expressed in mixed number form, with the quotient as the integer, the remainder as the numerator, and the divisor as the denominator.

Steps to form the simplest form of fractions with Improper Fractions

• Find the numerator’s and the denominator’s greatest common factor (HCF).
• HCF is divided by the numerator and denominator.

 In order to reduce the improper fractions completely we convert the improper fractions to mixed fractions. Here are the steps to convert improper fractions to mixed fractions

• Divide numerator by denominator.
• Put the outcome down as a whole number.
• Any leftover amount should be used as the fraction’s numerator.
• The numerator remains constant.

Some Examples of the Simplest Form of Fractions

Example 1

Reduce the fraction illustrated in figure 2

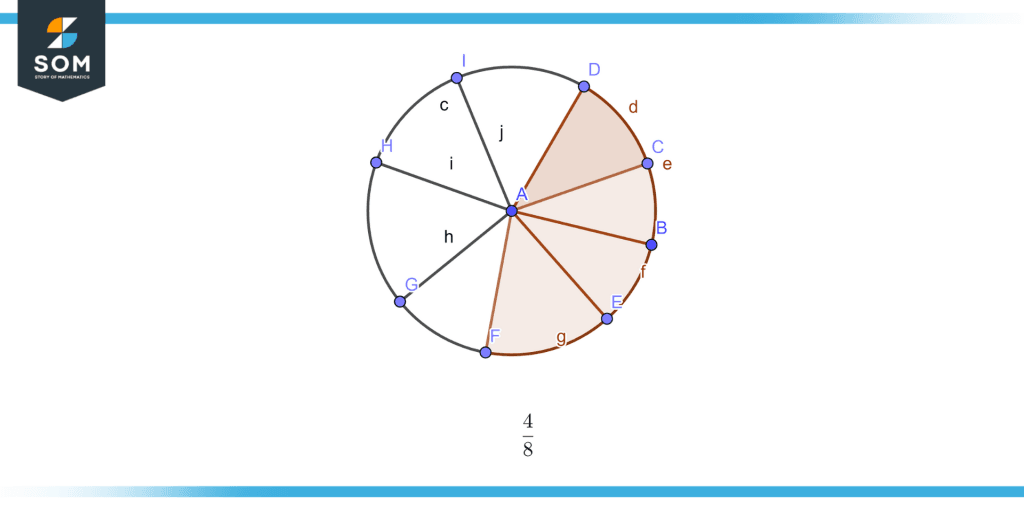
Figure 2 – Fraction

Solution

We can reduce the fraction if we take four common from both the numerator and denominator then $\dfrac{1}{2}$ will be the reduced fraction illustrated in figure 3.

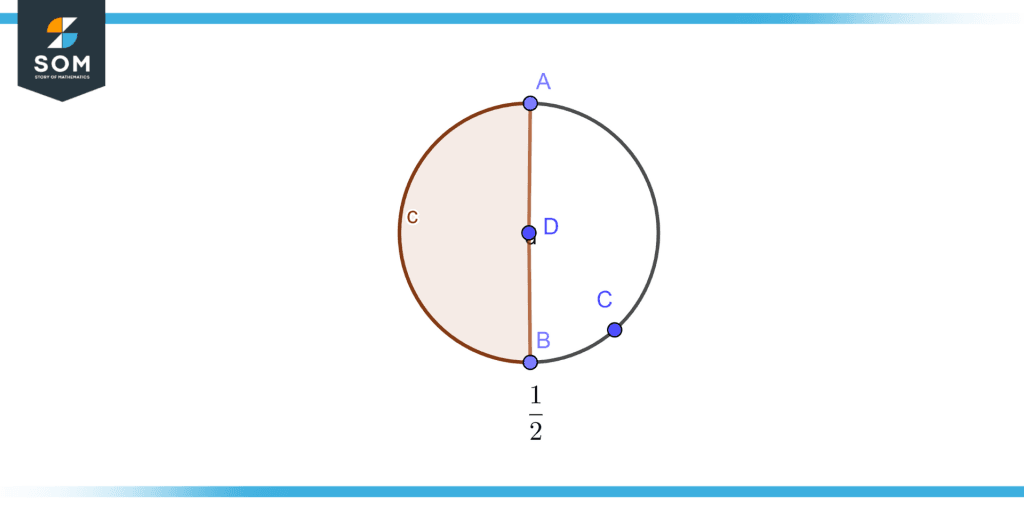
Figure 3 – Reduced fraction

Example 2

Reduce the following fractions

a) $\dfrac{15}{35}$

b) $\dfrac{4}{16}$

c) $\dfrac{3}{6}$

Solution

a) For reducing fractions, we take the highest common factor (HCF) of fifteen and thirty-five. The HCF of fifteen and thirty-five is five.

$\dfrac{3 \times 5}{7 \times 5}$ which is equal to $\dfrac{3}{7}$

b) For reducing fractions, we take the highest common factor (HCF) of four and sixteen. The HCF of four and sixteen is four.

$\dfrac{1 \times 4}{4 \times 4}$ which is equal to $\dfrac{1}{4}$

c) For reducing fractions, we take the highest common factor (HCF) of three and six. The HCF of three and six is three.

 $\dfrac{1 \times 3}{2 \times 3}$ which is equal to $\dfrac{1}{2}$

Example 3

Check whether $\dfrac{7}{15}$  is in reduced form or not.

Solution

We find the factors of seven and fifteen:

Seven: 1,7

 Fifteen: 1,3,5,15

One is the only common factor.

So, $\dfrac{7}{15}$ is in its original reduced form.

Example 4

Reduce $\dfrac{12}{18}$  to simplest form.

Solution

Factors of twelve are 1,2,3,4,6,12

Factors of eighteen are 1,2,3,6,9,18

the highest common factor (HCF) is six, so the fraction will be:

\[\dfrac{6 \times 2}{6 \times 3}\]

Which will be equal to $\dfrac{2}{3}$ hence the reduced form of $\dfrac{12}{18}$ is:

$\dfrac{2}{3}$

Example 5

Reduce the following fractions in reduced form.

a) $\dfrac{yz^2}{2z}$

b) $\dfrac{3^2}{3^5}$

Solution

a) Express both numerator and denominator in the form of product as the original fraction is a mixed variable.

      $\dfrac{y \times z \times z}{2z}$

As we can see z from numerator tor and z from denominator cancel out so the reduced fraction will be equal to:

$\dfrac{yz}{2}$

b) Express both numerator and denominator in the form of product as the original fraction is a mixed variable.

$\dfrac{3 \times 3}{3 \times 3 \times 3 \times 3 \times 3}$

As we can see nine from numerator and nine from the denominator cancel out so the reduced fraction will be equal to $\dfrac{1}{27}$.

All images/mathematical drawings were created with GeoGebra.

Simplest Form Algebra Definition < Glossary Index > Simultaneous Equations Definition