JUMP TO TOPIC
Simultaneous Equations|Definition & Meaning
Definition
“Simultaneous” means to occur at the same place or time. Simultaneous equations are defined as a group of equations with a common set of variables. They are also known as a system of equations and are used together to find a solution for unknown variables.
Simultaneous Linear Equations
Simultaneous linear equations have all the variables with a power/degree of one. Consider the two simultaneous equations given below:
5x – 4y = 21
3x + 5y = 20
Both equations have the variables x and y common in them.
The solution of the two equations is the values of (x, y) which satisfy both the linear simultaneous equations. Figure 1 shows the graph for the above equations.
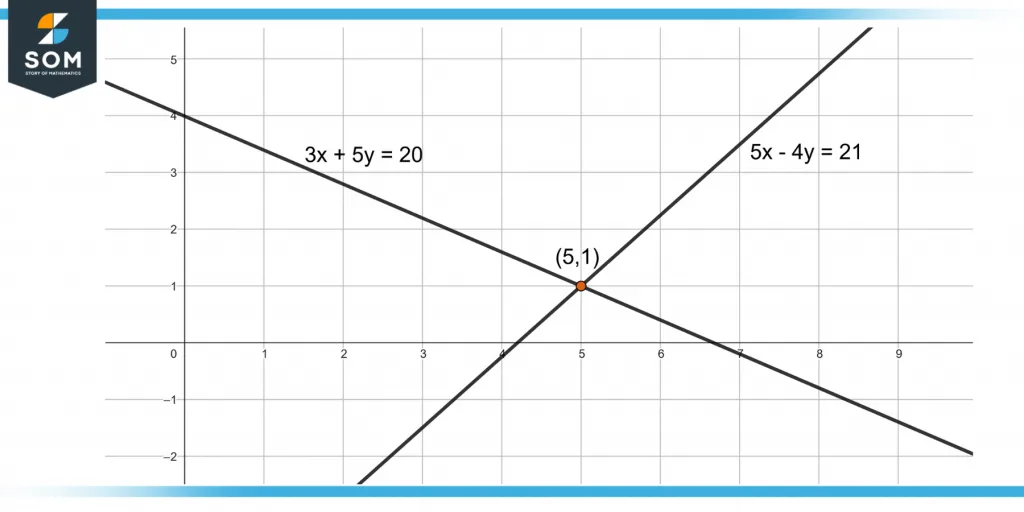
Figure 1 – Plot of Two Linear Simultaneous Equations
In figure 1, point (5,1) is the solution of the above simultaneous equations.
Point of Intersection
The point of intersection is where the two linear simultaneous equations or lines cross each other. This is the solution that satisfies both simultaneous equations.
In figure 1, the point (5,1) is also known as the point of intersection.
A set of two simultaneous equations with two variables x and y have their point of intersection in the x-y plane.
Similarly, three simultaneous equations with three variables will have an intersecting point or solution in the x-y-z space.
Simultaneous Equations in Matrix Form
Simultaneous equations can also be written in matrix form. Consider the three simultaneous equations given below
2x – 5y +4z = 10
3x + 7y – z = 16
6x + 3y +8z = 20
Figure 2 shows these simultaneous equations in matrix form.
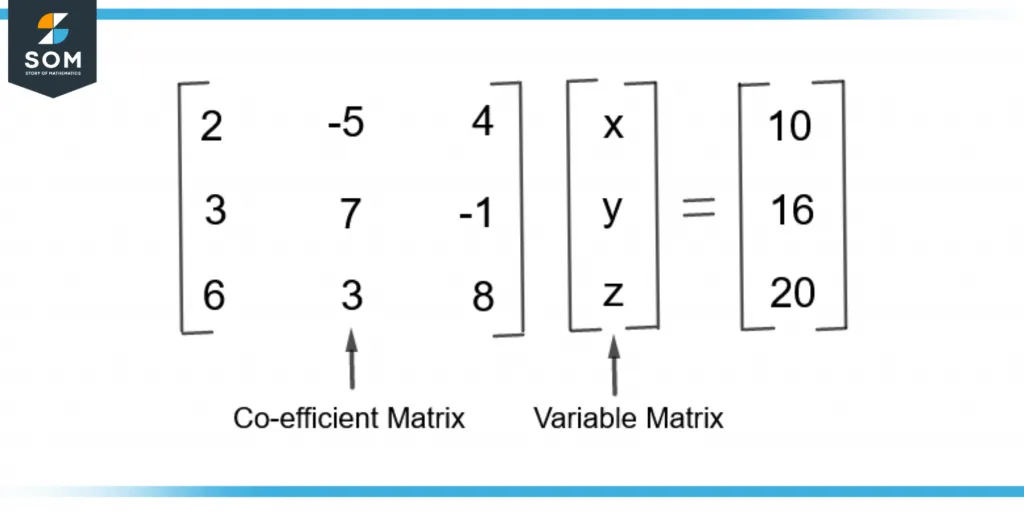
Figure 2 – Three Simultaneous Equations In Matrix Form
The matrix equation in figure 2 can also be written as:
CX = D
Where C is the co-efficient matrix and D is the variable matrix. The system is solved for the variables x,y, and z.
Through matrices, the simultaneous equations can be solved by using the above equation as follows:
X = $C^{-1}$.D
Where $C^{-1}$ is the inverse of matrix C. It is obtained by using the formula given below:
\[ C^{-1} = \frac{adj \ C}{det \ C} \]
Where “adj C” is the adjoint of C and “det” stands for determinant.
Methods To Solve Simultaneous Equations
The simultaneous equations are solved by finding a solution that satisfies all the equations.
To solve the equations, the number of variables in the equations should be equal to the number of simultaneous equations.
The following methods are used for solving simultaneous equations.
Elimination Method
In the elimination method, a variable from two simultaneous equations is removed or eliminated to obtain a one-variable equation.
This is done by adding or subtracting the equations with the same coefficients of the variable being eliminated.
The addition is performed when the coefficients of the variable have opposite signs and subtraction is done when the co-efficient signs are the same to eliminate the variable.
Multiplication can also be done on an equation to have the same coefficient of the eliminating variable.
Substitution Method
The substitution method is convenient when the equations are not adding or subtracting to cancel out a variable.
In this method, one of the two simultaneous equations is written in such a way with the substitution variable on one side and the rest of the terms on the other side.
This is then substituted into the second equation to form a one-variable equation. It is solved for the variable’s value.
A set of three simultaneous equations will have the substitution process twice.
Graphing
The two linear simultaneous equations can also be plotted on the graph to acquire the solution.
Some values of y are calculated from the equations with known x values. The points are plotted to get two lines for the two linear equations. The lines coincide at a point (x,y) which is the required solution.
Types of Solutions
Simultaneous equations can have the following types of solutions.
One Solution
Two simultaneous equations can have a single solution if there is one point of intersection between the two lines. It means that there is only one point that satisfies both equations.
Figure 3 shows two equations that have one solution.
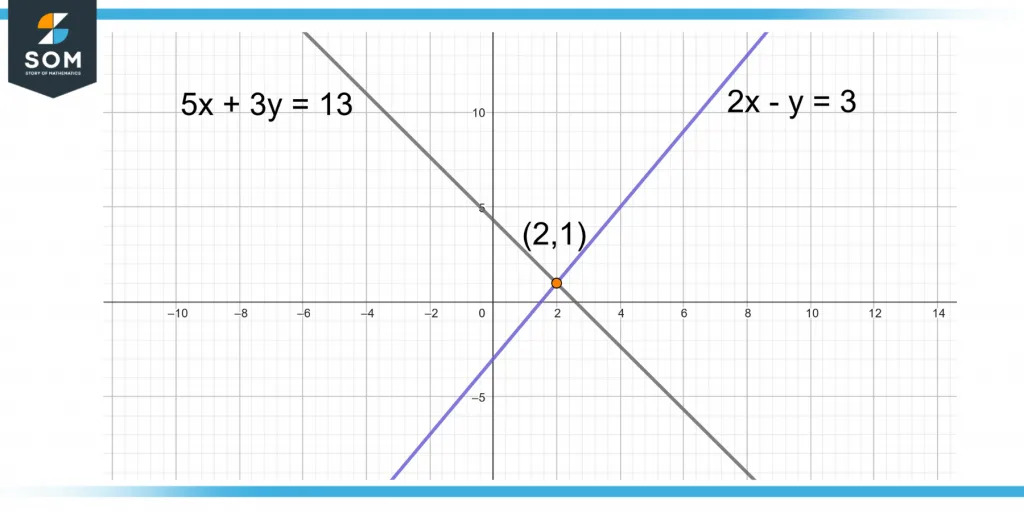
Figure 3 – Simultaneous Equations With One Solution
The solution is (2,1).
No Solution
Simultaneous equations can also have no solution if they are not crossing each other at some point. These linear equations are parallel to each other.
Figure 4 shows the plot of two equations with no solution.
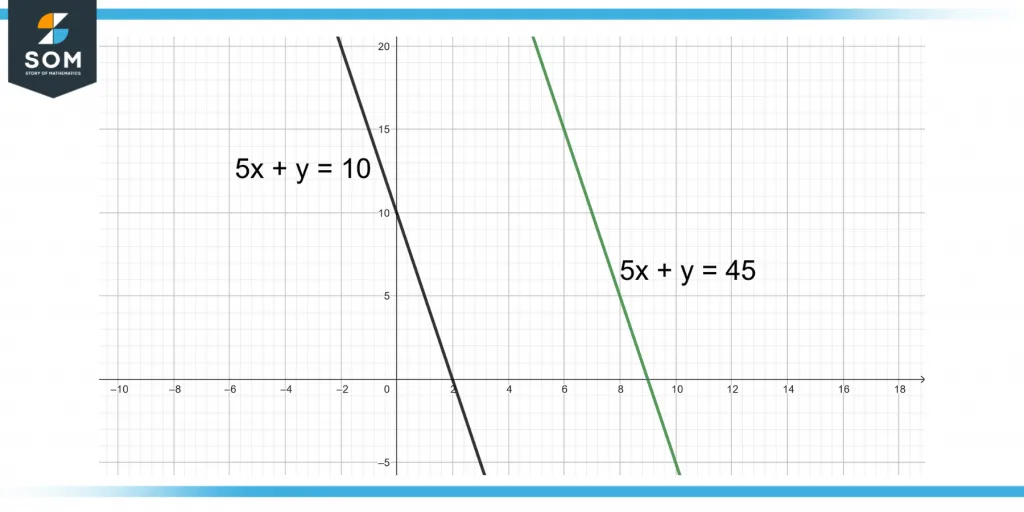
Figure 4 – Simultaneous Equations With No Solution
Infinite Solutions
There can be infinite solutions to simultaneous equations. This occurs when one equation is multiplied by a common multiple to form the other equation.
Figure 5 shows infinite solutions of the following simultaneous equations given below:
4x + y = 7
16x + 4y = 28
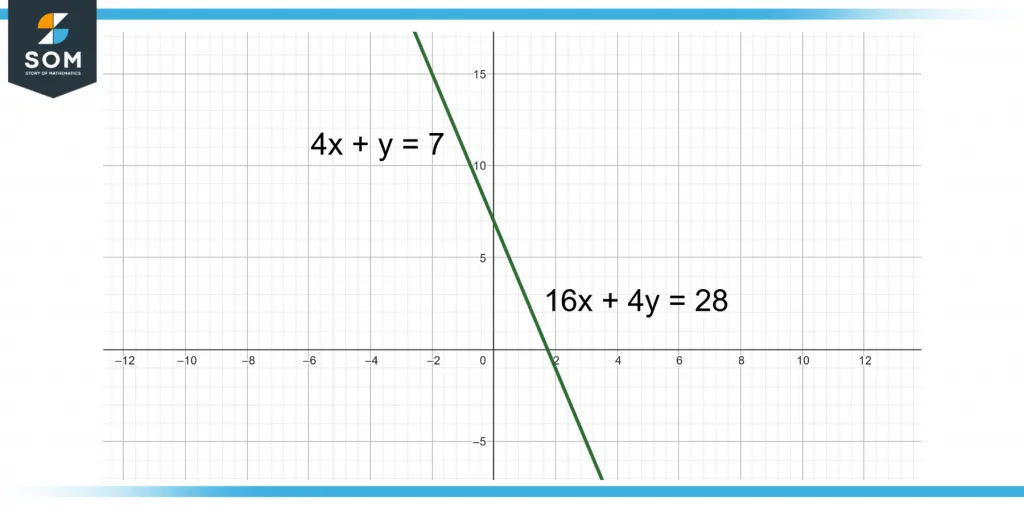
Figure 5 – Simultaneous Equations With Infinite Solutions
Notice that the first equation is multiplied by 4 to get the second equation. These two lines are one over the other on the graph.
Example Problem of Simultaneous Linear Equations
Consider the simultaneous equations:
8x + 3y = 108 … eq-1
10x – 15y = -90 … eq-2
Find the solution by using the elimination method. Also, show the point of intersection on the graph.
Solution
To eliminate y, the first equation is multiplied by 5 to have y with the same coefficients.
5( 8x + 3y = 108 )
40x + 15y = 540 … eq-3
Adding equations 2 and 3 gives:
10x – 15y + 40x + 15y = -90 + 540
50x = 450
With y eliminated, the value of x can be found by dividing both sides by 50:
x = 9
To find the value of y, put the value of x in equation 1:
8x + 3y = 108
8(9) + 3y = 108
72 +3y = 108
72 – 72 +3y = 108 – 72
3y = 36
Dividing by 3 into both sides gives the value of y as:
y = 12
So, the solution of the simultaneous equations is (9, 12). Figure 6 shows the plot of simultaneous equations and their intersecting point.
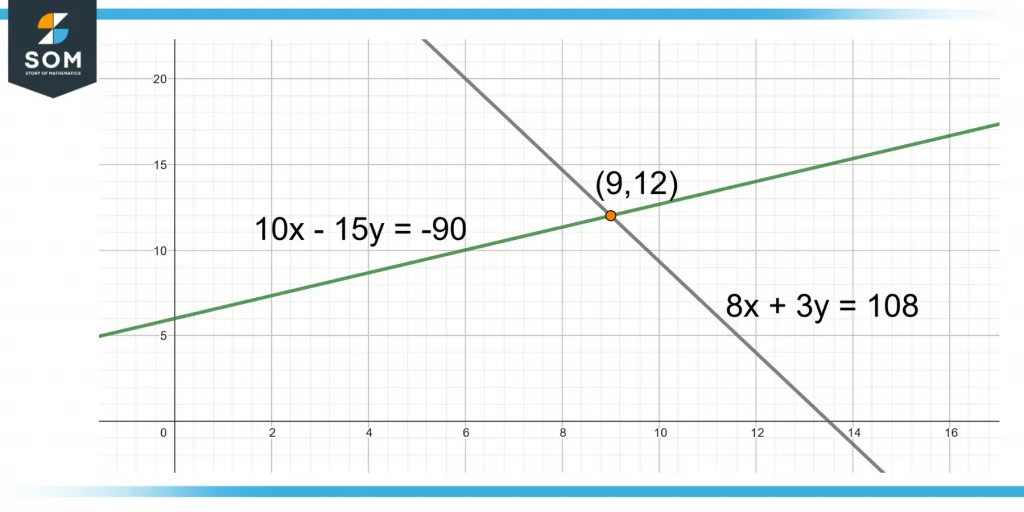
Figure 6 – Simultaneous Equations and their Intersecting Point (9,12)
All the images are created using GeoGebra.
