Sinh|Definition & Meaning

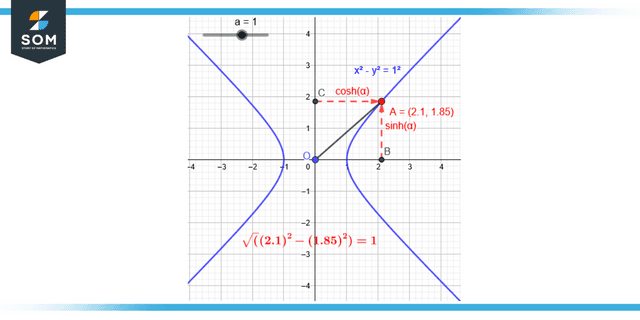
Figure 1: Graphical representation of hyperbolic function.

What Is a Hyperbolic Function?

Similar to the circle and trigonometric functions, the hyperbolic functions also have their own analogues. The hyperbolic function is utilized in the resolution of linear differential equations, determining distance and angle in hyperbolic geometry, and solving Laplace’s equations using cartesian coordinates. 

In most cases, the hyperbolic function will be performed in the area of the actual argument, which is referred to as the hyperbolic angle. The following are the fundamental hyperbolic functions:

• Sine of a hyperbolic curve (sinh)
• The cosine of hyperbolic arcs (cosh)
• Tangent in hyperbolic form (tanh)

The additional functions, such as the hyperbolic cosecant (cosech), hyperbolic secant (sech), and hyperbolic cotangent (coth) functions, are derived from these three fundamental functions.

In this article, we will discuss the hyperbolic function of sine, that is, sinh.

Applications of Hyperbolic Functions in Everyday Life

You and your companion intended to stroll to the theatre together, but it is now five minutes before the show’s start, and he is nowhere to be found. Suddenly, he is jogging on the sidewalk right in front of your house, and pausing to talk to you is not on his list of priorities at this time. You spring down from your porch and immediately begin to run.

As you get closer to your friend, you keep switching lanes until you finally catch up to them. Your friend observes as they look back at your footprints, saying, “Hey, you sketched out an interesting curve.” Which is followed by your response of “Of course.” The foundation of it is found in hyperbolic functions.

Okay, you most likely wouldn’t have said anything like this. That is after you have finished learning everything in this session.

Hyperbolic functions can be found in a wide variety of contexts. Let’s talk about their characteristics and some of the great things that can be done with them.

What Exactly Is the Function of Sinh?

The Sinh function is the hyperbolic counterpart of the Sin circle function, which is utilized throughout trigonometry. Real numbers define it by assuming that the area equals twice the axis and that a ray traveling through the origin will intersect the unit hyperbola. In addition, it is implemented when working with the ordinary differential equations of the second order.

The Function of the Hyperbolic Sine

The following is the definition of the hyperbolic function f(x) = sinh(x):

\[ \mathsf{\sinh(x) = \frac{e^x−e^{−x}}{2}} \]

This function fulfills the requirement that:

sinh (-x) = – sinh x, and sinh 0 = 0 at the same time.

They are similar to the trigonometric functions in several respects, and their relationship to the hyperbola is comparable to the trigonometric functions’ relationship with the circle. Because of this, they are referred to as hyperbolic functions as a group, while their components are referred to as hyperbolic sine, hyperbolic cosine, and so on.

Functions in an Inverse Hyperbolic Form

Inverse hyperbolic functions are the name given to the functions that are the opposite of hyperbolic functions. In some circles, it is also referred to as the area hyperbolic function. The hyperbolic angles that correspond to a particular value of the hyperbolic function are returned by the inverse hyperbolic function when that function is called.

The symbols sinh^-1, cosh^-1, tanh^-1, csch^-1, sech^-1, and coth^-1 design these functions, respectively. The following is a definition of the reverse hyperbolic function in the complex plane:

• Sinh-1 x = ln(x + √[1+x2])
• Cosh-1 x = ln(x + √[x2-1])
• Tanh-1 x = (½)[ln(1+x) – ln (1-x)

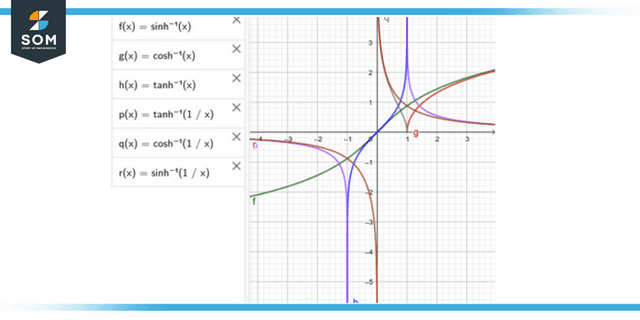
Figure 2: Representation of inverse of the hyperbolic function.

Characteristics of the Functions of Hyperbolas

Similarities can be seen between the properties of trigonometric functions and those of hyperbolic functions. Among them are the following:

• sinh(-x) = -sinh(x)cosh(-x) = cosh x
• sinh(2x) = 2 sinh(x)cosh(x)
• cosh(2x) = cosh²(x) + sinh²(x)

The following are examples of derivatives of hyperbolic functions:

• d/dx sinh (x) = cosh x
• d/dx cosh (x) = sinh x

The following is a list of several relations between the hyperbolic function and the trigonometric function:

• Sinh x = – i sin (ix)
• Cosh x = cos (ix)
• Tanh x = -i tan (ix)

What Exactly Are the Terms sinh(x) and cosh(x)?

Take note that sinh(x) is an odd function just like sin(x), which indicates that f(-x) equals -f(x), and cosh(x) is an even function just like cos(x), which indicates that f(-x) equals f. (x). Additionally, since ex = sinh(x) + cosh(x), the two fundamental hyperbolic functions, which are also components of the exponential function, is odd and even, respectively,

Differences Between Sin and Sinh

Radians are used to measure any angles. The cyclic sine of the components of X can be represented by the function sin(X). sinh(X) represents the hyperbolic sine of X’s constituent parts.

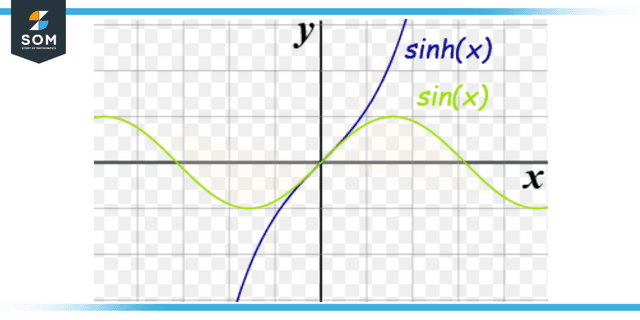
Figure 3: Graphical representation of difference between sinh and sin.

Examples of Sinh

Example 1

Show that sinh (x + y) = sinh x cosh y + cosh x sinh y

Solution

sinh (x + y) = [e ^{x + y} – e ^{–x –y}] / 2

= [2e ^{x + y} – 2e ^{–x –y}] / 4

= [2e ^{x + y} + (e ^{x – y} – e ^{y – x}) – (e ^{x – y} – e ^{y – x}) – 2e ^–x e ^–y] / 4  

= [(e ^{x + y} + e ^{x – y} – e ^{–x –y} – e ^{y – x}) / 4] + [(e ^{x + y} –e ^{x – y} + e ^{y – x} – e ^{–x –y}) / 4]

= [(e ^x – e ^–x) / 2] [(e ^y + e ^–y) / 2] + [(e ^x + e ^–x) / 2] [(e ^y – e ^–y /2)]

= sinh(x)cosh(y) – cosh(x)sinh(y)

Hence it is proved.

Example 2

Show that cosh² x – sinh² x = 1

Solution

L.H.S:

= [(e ^x + e ^–x) / 2] ² – [(e ^x – e ^–x) / 2] ²

= [(e ^2x + 2 + e ^-2x) / 4] – [(e ^2x – 2 + e ^-2x) / 4]

= 4/4 = 1 = R.H.S

So, the left-hand side is equal to the right-hand side.

Hence proved.

All images/graphs are created using GeoGebra.

Simultaneous Equations Definition < Glossary Index > Sinusoid Definition