Sinusoid|Definition & Meaning

Sinusoids, also known as sinusoidal waves or simply sine waves, are mathematical curves that are described in the form of the sine trigonometric function, whose graph the sinusoid represents. 

It can be thought of as a form of a continuous wave as well as a continuous periodic function. Sinusoids are frequently used in the field of maths and also in the areas of physics, signal processing, engineering, and a great number of other fields.

The sinusoid can be expressed mathematically in the form of the following formula:

y(t) = A sin(2πft + φ)

In this formula, the letter A stands for the amplitude of the wave, which can also be considered the wave’s highest divergence from the horizontal plane. The letter f expresses frequency, which is determined in hertz and is defined as the number of oscillations that take place in a given amount of time (Hz).

The letter t stands for the time, whereas the symbol φ denotes the phase shift, also described as the movement of the wave in a horizontal direction along the time axis. Since Sinusoids are examples of periodic functions, this means that their pattern is repeated after a predetermined amount of time.

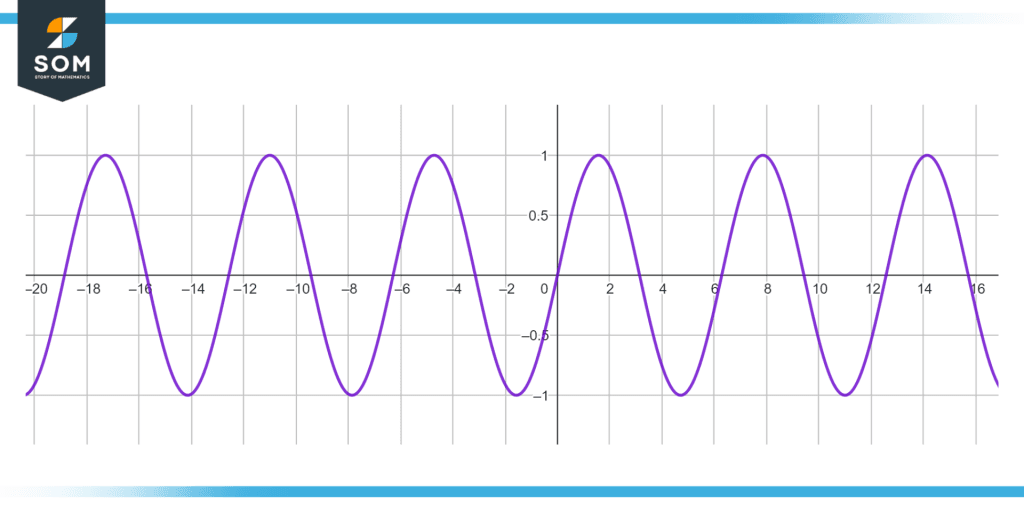
Figure 1: Illustration of Sinusoid

Characteristics of Sinusoid

Below we will discuss in detail the following key characteristics of sinusoids.

• Amplitude of sinusoid
• Frequency of sinusoid
• Period of a sinusoid
• Phase Shift of a sinusoid

Amplitude of Sinusoid

A sinusoid’s amplitude can be thought of as a measurement of the highest amount that the wave deviates from its horizontal axis. It is denoted by the alphabet “A” in the formula we discussed above: y(t) = Asin(2πft + φ).

The amplitude is often determined with the same unit as that of the dependent variable (y), and it is responsible for determining the height of the wave, also known as how much the wave goes above and beneath the horizontal plane.

A wave that has a greater maximum value and a lower minimum value is the result of an amplitude that is larger, while an amplitude that is smaller leads to a wave that has a lower maximum value and a lower minimum value.

The amplitude of a sinusoid affects the wave’s overall shape as well as its function. A wave with a bigger amplitude is one that is more noticeable and has a more significant influence on its surroundings.

Frequency of Sinusoid

A sinusoid’s frequency can be understood as a measurement of the number of oscillations that take place in a given amount of time. The unit of measurement used to determine the frequency of a sinusoid Hertz (Hz), which is the reciprocal of the period (we will discuss more regarding what exactly a period is in the later part of this article).

The consequence of a wave with high frequencies is that it oscillates a greater number of times in a given amount of time, while the effect of a wave with low frequencies is that it oscillates a lesser number of times in a given amount of time.

A sinusoid’s frequency seems to have an effect not only on the wave’s general form but also on its behavior; a greater frequency results in a wave that varies more quickly and has a greater pitch than one with a lower frequency.

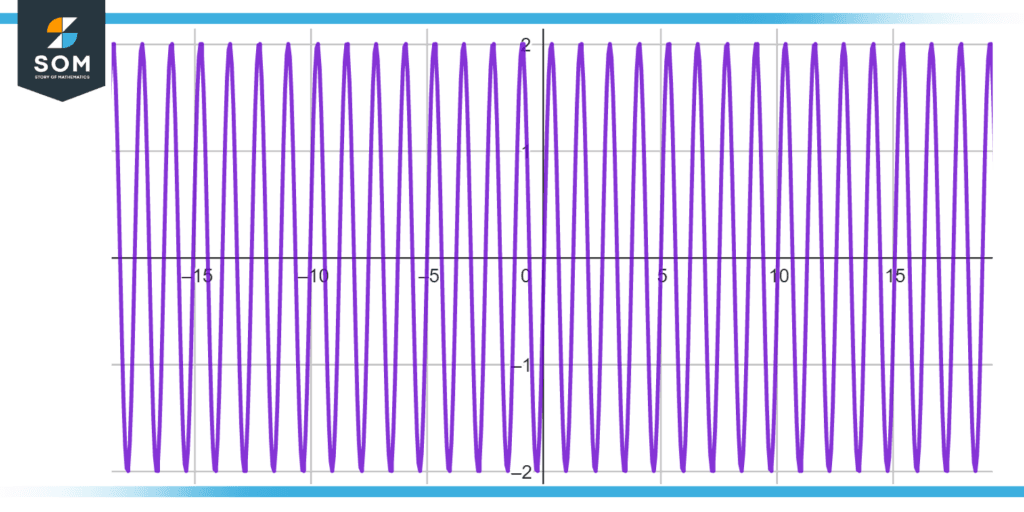
Figure 2: Illustration of Frequency of Sinusoid

Period of Sinusoid

The amount of time that passes before a sinusoid can be said to have gone through one complete oscillation is referred to as its period. It is denoted by the symbol “T” and is described as the inverse of the frequency, which is mathematically expressed through the following equation:

T = 1/f

The length of time required for the wave to travel from its maximum height to its lowest point and then back up to its highest point once more is indicated by the wave’s period. A wave with a shorter period will oscillate more rapidly, while a wave with a longer period will oscillate more slowly.

This is because the shorter the period, the faster the wave will move. The period of a sinusoidal wave is an essential property that determines the wave’s general structure as well as its conduct.

Phase Shift of a Sinusoid

A sinusoidal wave’s phase shift can be thought of as a measurement that indicates how far horizontally the wave is displaced in comparison to a reference wave. In the equation y(t) = A sin (2ft + φ), it is denoted by the symbol “φ” and the unit of measurement for it is radians.

A sinusoidal wave’s phase shift causes the beginning position of the wave to shift, moving it either left or right direction along the horizontal axis. This causes the wave to appear to move in a different direction.

The wave will be moved to the right when there is a positive phase shift, and it will be moved to the left when there is a negative phase shift. The degree of the phase shift is what defines the extent of horizontal shift; a bigger phase shift will result in a larger amount of shift than a smaller phase shift will.

The phase shift of a sinusoid is a key property that impacts the wave’s general structure and conduct. It may also be used to control the time of several sinusoidal waves and synchronize them with one another.

Applications of Sinusoid

Sinusoidal functions are useful in a wide variety of contexts, including but not limited to the following disciplines.

Processing of Signals and Various Communication Methods

In the field of communication and signal processing, sinusoidal functions are frequently utilized to mimic a variety of communications, including sound and auditory signals, radio signals, and visual signals, amongst others.

Electrical Engineering and Alternating Current (AC) Circuits

In order to describe alternating current (AC) signals in electrical circuits, such as signals of currents and voltages in power systems and electrical machinery, sinusoidal functions are utilized.

Vibrations in Mechanical Systems and Control Systems

Sinusoids are utilized in the modeling of mechanical motions and oscillations in control systems. For example, the oscillation of a spring-mass setup or the motion of a pendulum can both be modeled using sinusoidal functions.

Applications in Biology and Medicine

A variety of medical and biological signals, such as those relating to pulse rate and brain function, can be modeled using sinusoidal functions.

In the Spheres of Science and Mathematics

Sinusoidal functions can be used to represent periodic processes in physics and engineering, solve differential equations, and analyze periodic data in domains such as economics and finance. These are just some of the many applications that can be found in mathematics and science.

These are just some of the numerous uses of sinusoidal functions that may be found in many different fields of research, but there are many more. Sinusoidal functions are an essential technique for simulating and comprehending periodic processes in a wide variety of domains because of their adaptability and the relative ease of their mathematical representation.

An Example of a Sinusoid

Using the information given in the equation below, find out the amplitude of the wave and explain what it means.

y(t) = 3 sin (2πft + φ)

Solution

Since we know that sinusoid can be expressed mathematically in the form of the following equation:

y(t) = A sin (2πft + φ)

“A” in the above equation refers to amplitude. Now we can find the value of Amplitude by comparing this equation with the one given in the example such that:

A = 3

Below is the graphical illustration of the amplitude calculated in this example.

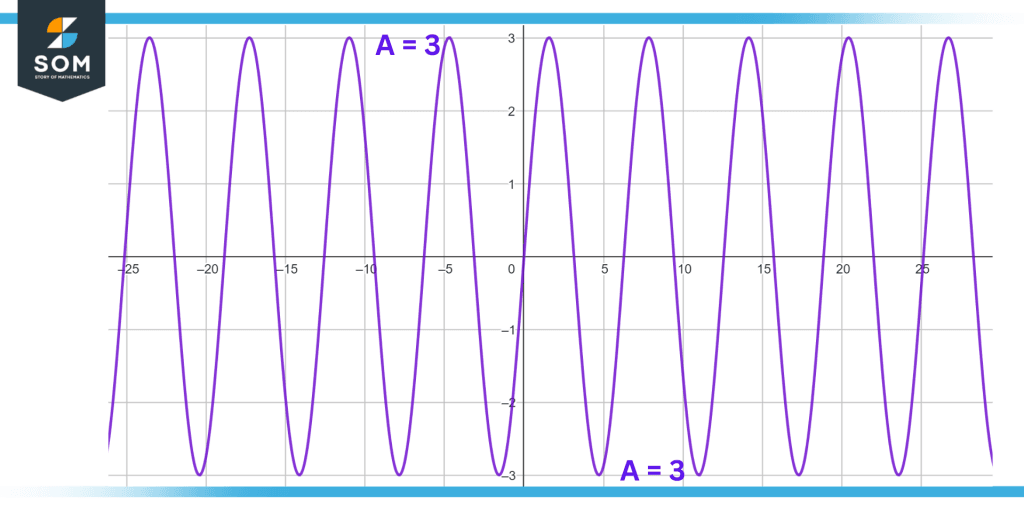
Figure 3: Illustration of Calculated Amplitude

The value of amplitude implies that the wave will extend 3 units above and beneath the horizontal plane.

All images/mathematical drawings were created with GeoGebra.

Sinh Definition < Glossary Index > Skewed Data Definition