JUMP TO TOPIC
Subscript|Definition & Meaning
Definition
Any text is said to be in subscript if it is both smaller than and placed slightly lower than the rest of the text. Subscript has various uses in mathematics, especially in denoting multiple variables and lengthy operations. Instead of assigning each variable a new letter, we can keep one letter and use subscripts as in x$_1$, x$_2$, and so on (pronounced “x one” or “x sub one”).
Further Explanation
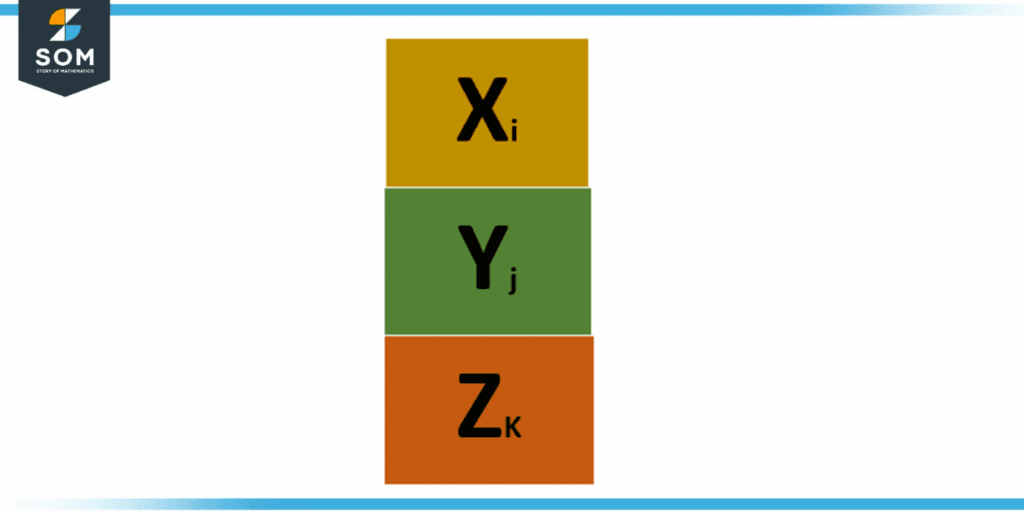
Figure 1 – Subscript
In the figure above, we have Xi, Yj, and Zj. Here, i, j, and k are the subscripts, and they are represented by the small font letter below the text line.
Subscript is an abbreviation for “subscript,” which describes words or symbols that are printed lower than normal text and are half the length of a standard character. Subscript text is used in examples like the one below, where the words “Subscript Text” are placed midway below the line of “Normal Text.”
Subscript is useful not only for its aesthetic qualities but also in a few other contexts. In math and science, a subscript can be used to define variants of the same variables or to identify specific individuals within a set or sequence. A subscript is a very small letter just below the line of text.
The related term “superscript” refers to letters that are written slightly above and to the right of the standard line of type. This is in contrast to subscripts, where the letters are written just a little bit under the certain line.
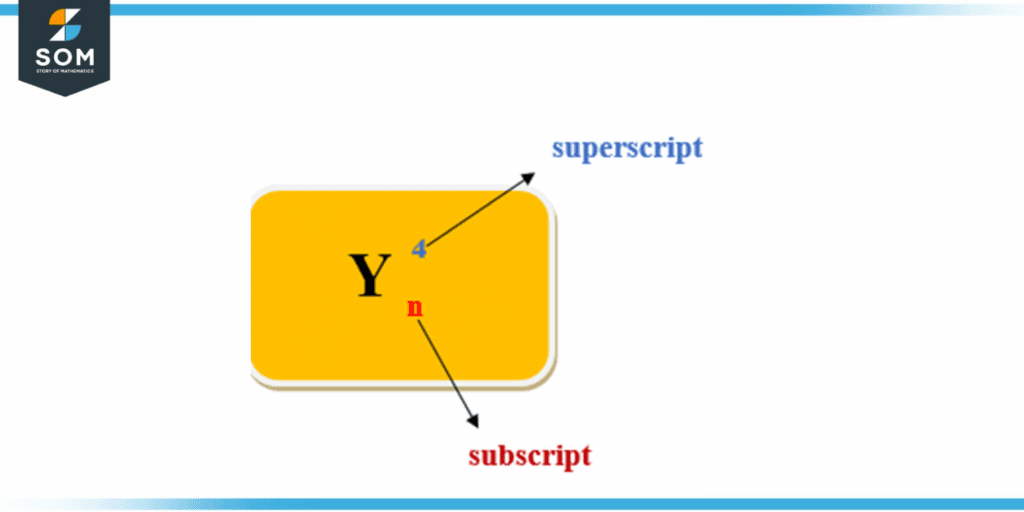
Figure 2 – Subscript and Superscript
In the figure above, the subscript is a small letter just below the line of text. That is, “n,” and superscript is a letter just above the line of, i.e., “4.“
Studies of language also involve the use of smaller letters. For instance, linguists have something called the International Phonetic Alphabet, which is a unique set of symbols that represent the pronunciation of spoken languages (IPA), Gracias is transcribed as /a.j as/, and if you’ve ever studied a language other than English, you’ve probably come across this spelling at some point.
Characters such as small type, subscript and superscript symbols, and other symbols aid in representing distinct specific characteristics of the pronunciation, as well as a variety of additional sounds, side tones, and tiny changes in the transmission of sound.
Subscript in Equations
The subscript [work type] may stand for the various occupations represented in an organization, whereas [location] may indicate the precise location of a given office or manufacturing facility. Consider the equation:
hires (job category, workplace) = wanted hires (job category, workplace) / time to recruit
worker (job category)
In this case, the equation permits a singular equation to determine the staffing needs of any enterprise, regardless of industry or place. It is important to note that the above equation accounts for differences in hiring time-based on work type but not geography.
The subscript is a value used to identify a specific occurrence in an array in programming. For instance, in the notation example [3] or $example [3], “[3]” refers to a specific index within the “example” array.
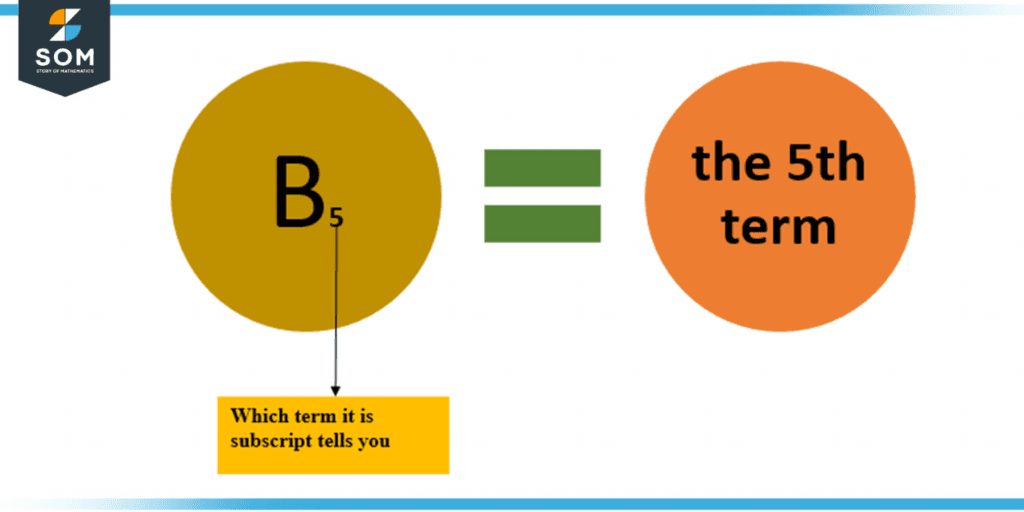
Figure 3 – Subscript terms
Here in the above figure, in B5, the letter “5” represents which term of B it is.
Subscript in Functions
Equations can be manipulated in a variety of different ways using the special functions that subscripts provide. The SUM function computes the total of all the variables of a subscript that has an exclamation point (!) in front of it. Product, maximums, and minimums are some examples of other functions.
For example, consider the entire working population of the US. We can categorize them according to the type of work that they do and the state they work in. Then, if we have to total the workers for a specific type of work, we must sum up the workers across all the states that perform that specific type of work:
TOTAL WORKERS[work_type] = SUM(Workers[work_type, location!])
This equation outlines the process of adding up the number of employees performing each specific sort of job (such as office staff or plant operators) across all the locations. In other words, the total number of office workers across all sites, as well as the total number of plant operators across all locations.
In this example, since location is denoted by an exclamation mark, the total function can be applied to the subscript “location” with a fixed work type.
Subscript as Trademark Symbol
Superscript letters can be used to create the trademark symbol (CompanyTM, for example). Other brands like Coca-Cola and Starbucks place their trademark symbols as subscripts next to the brand name or logo. A general trend is to place the trademark symbol in subscript if the brand’s face is a logo, and in superscript if it’s a word or phrase (e.g., Gillette), though there are exceptions.
The use of subscripts can make it possible to design a single item that is representative of a variety of distinct steps within the same physical phenomenon. For instance, a population aging chain is made up of numerous stocks, each of which people age in before moving on to the next stock in the chain.
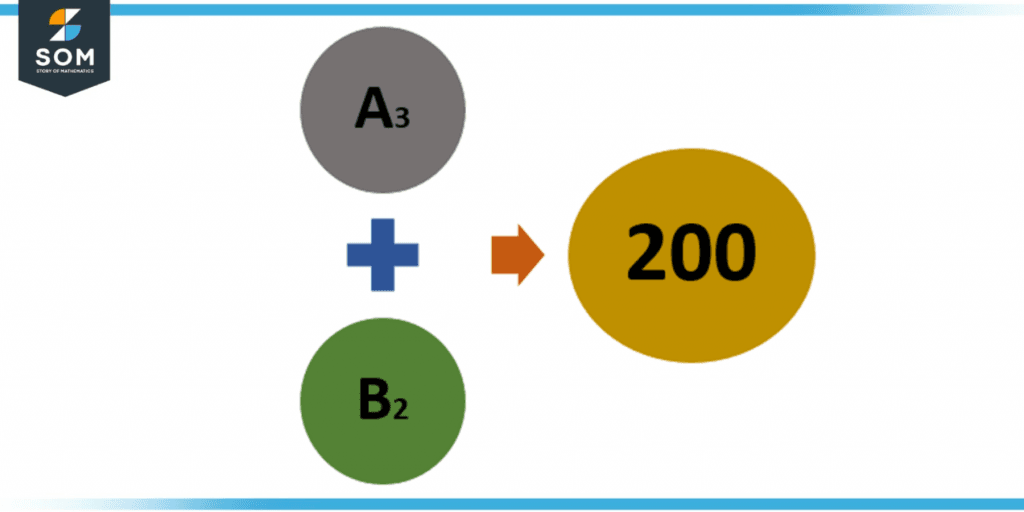
Figure 4 – Pictorial Presentation
Here in the above figure A3 and B2, in this equation, “2” and “3” are the subscripts that represent which term it is. Sub 2 means the 2nd term, and sub 3 means the 3rd term.
Examples of Subscripts
Example 1
What is a subscript in z2?
Solution
The number 2 in term z2 is the subscript (pronounced “z sub 2″ or just “zee-two”)
Example 2
In the term Yn, what is the subscript?
Solution
The number n in the term Yn is the subscript (pronounced “y sub n” or just” Y n”).
Example 3
Separate the subscripts in the term XiYj. If X and Y were vectors with k components, what is the significance of these subscripts?
Solution
In the above term XiYj, i and j are the subscripts. If we think about X and Y as k-dimensional vectors with components 1, 2, 3, …, k, then “i” represents the ith component of X where i $\leq$ k, and “j” represents the jth component of Y, where j $\leq$ k.
All the above figures are created on GeoGebra.
