JUMP TO TOPIC
Substitution|Definition & Meaning
Definition
In an algebraic equation, substitution refers to the process of replacing the variables, which are represented by the letters, with the corresponding numerical values. After that, we are able to compute the overall worth of the expression.
The substitution method is one of the algebraic approaches that can be utilized in the resolution of a linear equation system involving two variables. Using this approach, the number of any of the variables may be determined by isolating that variable on one aspect of the equation and extracting all of the other terms from the opposite of the equation.
After that, we enter that value as a substitution within the second equation. Finding the answers to a set of linear equations using the substitution method is a straightforward process that requires only a few easy steps.
The following figure explains the substitution method graphically. Suppose that we want to add the three objects as shown in the figure. By substituting the values of three objects we end up with a value of 12.
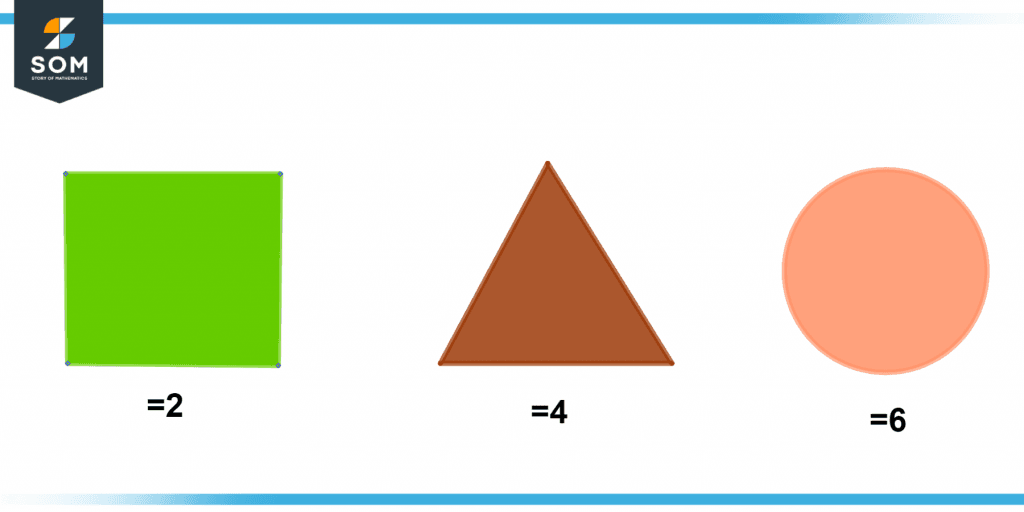
Figure 1 – Graphical explanation of the substitution method
The Definition of the Substitution Method
The algebraic solution to the problem of solving simultaneous linear equations is called the substitution method. In this approach, the value of a variable taken through one equation is swapped into the second equation, just as the name of the method suggests.
Doing so converts a pair of linear equations into a single linear equation containing just one variable that can then be solved in a straightforward manner.
Try to achieve a basic understanding of the algebraic technique and the graphical method before moving on to solving linear equations with the substitution method. This will prepare you for the next step.
Using Algebraic Methods
Two-variable linear equations can be solved using a variety of algebraic techniques. The algebraic approach can be broken down into these three broad classes:
- Method of substitution.
- Method of elimination.
- Method of cross multiplication.
Graphical Methods
To solve a system of linear equations, one can utilize a technique that is also called the geometric method, and that is called the graphical method. In this approach, the equations are formulated in such a way as to take into account both the optimal solution and the constraints. This procedure has been carried out in a series of phases in order to find the solutions in order to solve the linear equations system.
Steps in the Substitution Method
For example, the solution to the system of two equations having two unknown values can be determined by following the procedures that are shown below. This section contains a list of the steps that must be taken in order to solve the linear equation. They represent:
- Expanding the brackets will help simplify the equation that has been presented.Find a solution for either x or y in one of the equations.
- In the other equation, substitute the solution from step 2 in its place.
- Now, using only the most fundamental arithmetic procedures, calculate the newly derived equation.
- Finally, the equation needs to be solved in order to determine the value of a second variable.
The Distinctive Features of the Elimination and Substitution Methods
As we know, the substitution approach entails solving one equation for the value of the variable in question and then substituting that value into the second equation. On the other hand, the elimination method involves removing unnecessary variables from an equation until the system is a function of a single one. The substitution approach can be used to find the values of x and y at the intersection point with precision.
Consequently, the key distinction between the substitution approach and the elimination method is that the former involves replacing the variable with such a value, and the latter involves erasing the variable from the linear equation system.
Important Remarks Regarding the Method of Substitution
- To begin using the substitution approach, pick an equation that has a coefficient of one for at least one of the variables, and then solve for that variable. This will get you started with the procedure (with coefficient 1). Because of this, the process is simplified.
- Before beginning the replacement process, merge any phrases that are the same (if any).
- After we have determined the value of one variable, we may use either one of the following equations or even any equation we have encountered thus far to get the value of the second variable.
- Using the substitution approach to solve a problem, if we find any true statements as 3 = 3, 0 = 0, etc., when solving the problem, then this indicates that the system has an endless number of solutions.
- When solving a problem using the substitution approach, if we encounter any false statements such as 3 = 2, 0 = 1, etc., this indicates that the problem does not have a solution.
Graphical Explanation of Substitution
The following figure shows the arithmetic operations using the substitution method. By solving the below figure, we end up with a value of 14.
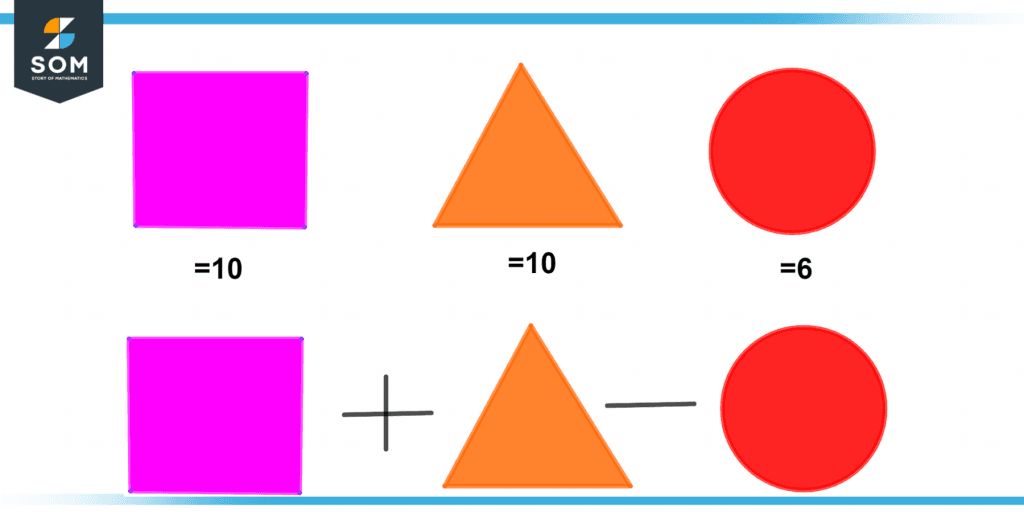
Figure 2 – Arithmetic operations using the substitution method
In the figure below, you can see how the substitution method is used to do the math. The rectangle value is 10, and the triangle value is 220. When we solve the figure below, we get the number 230.
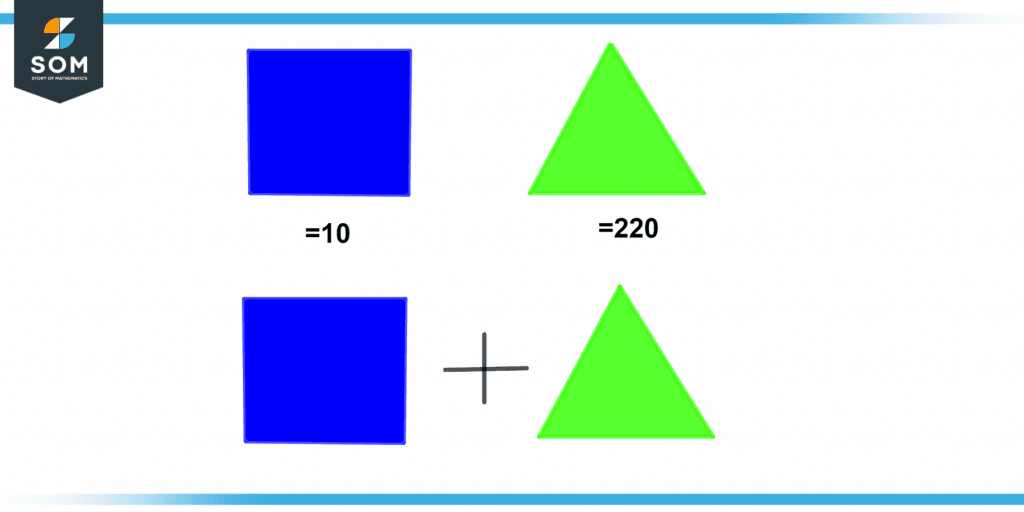
Figure 3 – Substitution method on two objects
Numerical Examples Using Substitution
Example 1
Find out what 10x – 5y equals when x = 20 and y = 4.
Solution
Given that:
x = 20
y = 4
The given equation is:
10x – 5y
By putting the values in the above equation, we get:
= 10(20) – 5(4)
= 200 – 5(4)
= 200 – 20
By subtracting, we get:
= 180
Example 2
Find out what 20x – 5y equals when x = 220 and y = 40.
Solution
Given that:
x = 220
y = 40
The given equation is:
20x – 5y
By putting the values in the above equation, we get:
= 10(220) – 5(40)
= 2200 – 5(40)
= 2200 – 200
By subtracting, we get:
= 2000
All images/mathematical drawings were created with GeoGebra.
