Subtended Angle|Definition & Meaning

What Is a Subtended Angle? 

A simple definition of subtended angle would be that it is an angle between two points. A more practical explanation is that if an object is placed at a distance from the viewer, then the lines that pass through the corners of that object will make an angle such that the measure of the angle depends on the distance between the object and the viewer.

If the shortest possible distance between the two increases, the subtended angle will tend to decrease, whereas it will increase if the distance keeps on decreasing.

In geometrical terms, such an angle can be formed by an arc, a certain segment, or any other curve that contains at least two corners or endpoints. The line segments that join the two endpoints of an arc, segment, or curve are sometimes called rays of an angle.

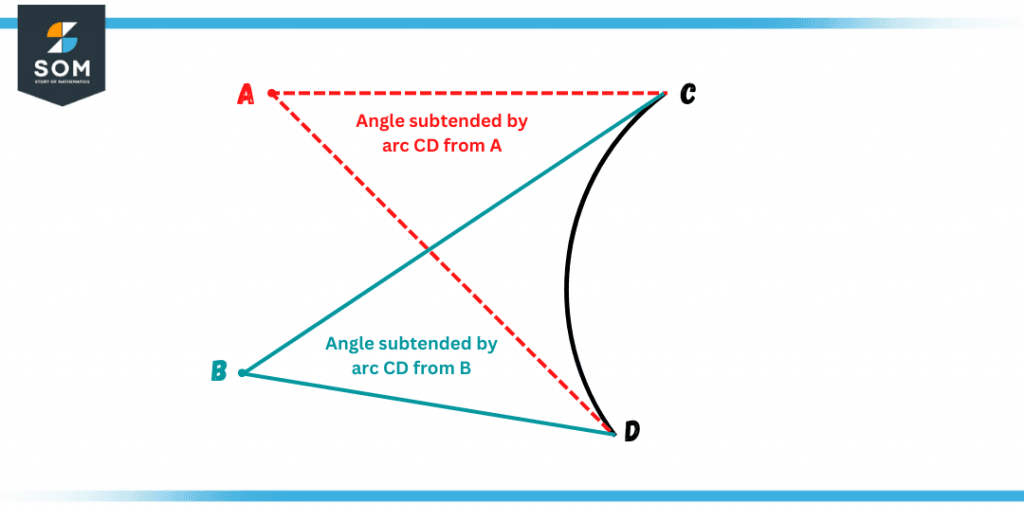
Figure 1 – Angles subtended by an arc from two points

The object that is contained inside these rays of an angle is thought of as the subtension of that subtended angle. Additionally, we will occasionally argue that angle intercepts or encapsulates a curve.

The definition of subtended angle alters with the context of the position. For example, you can say an angle made by an arc is subtended even if the vertex of the angle lies in the center of the circle.

What Is an Angle?

An angle is a measurement of a shape that is made by two lines going away from a shared point. This shared point is known as the vertex.

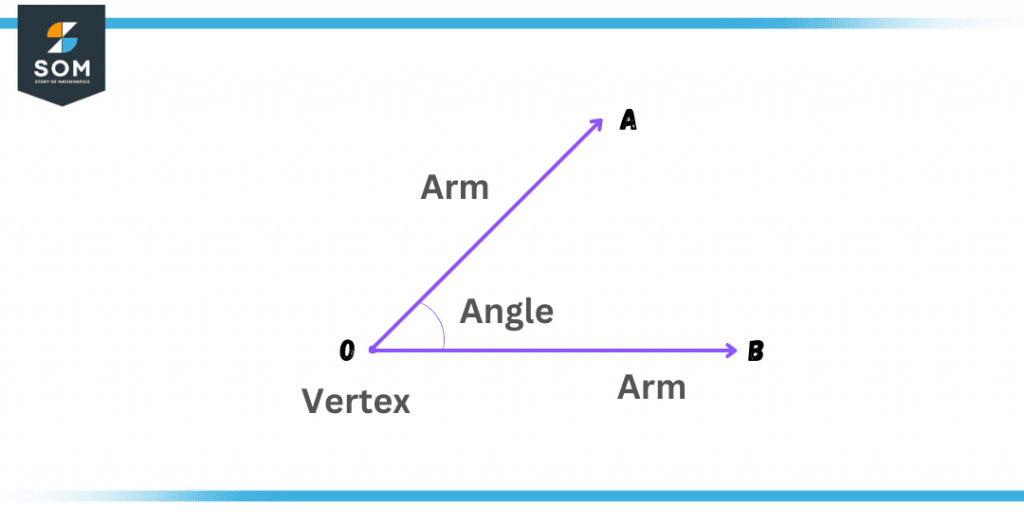
Figure 2 – A visual representation of an angle

An angle is represented by a unique symbol, $\angle$, whereas the angles are measured in degrees or radians.

It consists of 4 building blocks,

Vertex

The common point of the edge of an angle where the two rays or straight lines meet. Usually, the vertex is represented by the symbol ‘O’, as shown in the figure.

Arms

The two bars that extend from a common or shared point are known as arms. They form the two sides of an angle. In the above figure, OA and OB form the arms of an angle.

Reference

A straight line that is used as a reference for drawing an angle is known as a reference side or reference line. Here OB is the reference line.

Terminal

The ray that is used as a rotating arm for measuring the angle is known as the terminal line. This terminal ray decides how much the angle is formed. Here OA is the terminal line.

How To Find an Angle Subtended by an Arc?

Subtended angles are any of the several angles that may be created by merging the arcs’ ends in a circle. These arcs may be used to generate a variety of angles, including angles that are inside a similar section, angles that are within a curve, angles that intersect with the ring, etc.

An arc is a portion of a circle that is extracted from its circumference. The angle of that arc would be formed when two straight lines pass through the endpoints of the arc and meet at a shared point. As shown in the following figure, an arc is located on the circumference of the circle, and two distinct angles are formed from two different common points.

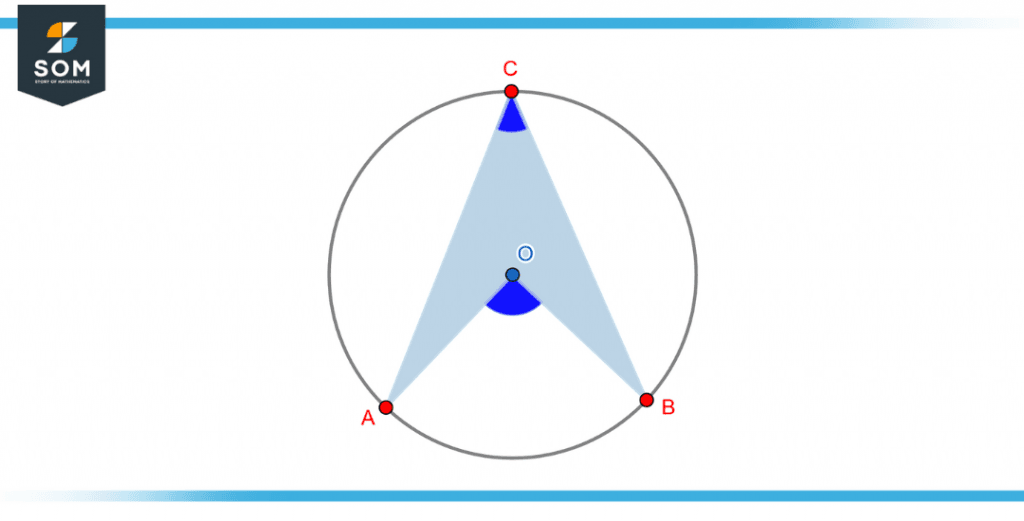
Figure 3 – Angle subtended by an arc at the center of a circle

Finding the angle that the arc subtends is based on a theorem that relates the angles formed from the center of the circle and at any other point on the circle‘s circumference.

The theorem says that the angle formed at the center of the circle is two times the angle that is formed anywhere on the circumference.

In the above figure, the same arc subtends two different angles, $\angle$AOB at the center and $\angle$ACB, at the tangent point C.

If we draw a perpendicular line from point C and point O, it will meet the other side of the circle at point D, thus making two triangles $\triangle$OAC and $\triangle$OBC.

In both triangles, one angle and one side are concurrent. Thus using the exterior angle theorem, we can prove that,

$\angle$AOD = 2 x $\angle$ACO

$\angle$DOB = 2 x $\angle$OCB

Adding the above equations gives:

$\angle$AOD + $\angle$DOB = 2 x ($\angle$ACO + $\angle$OCB)

$\implies$ $\angle$AOB = 2 x $\angle$ACB

This proves that any subtended angle on the circumference will be one-half of the angle formed at the center.

Subtended Angles of Different Objects

Moon

If a person looks up to a moon from the surface, the angle that is formed is 0.54$^{\circ}$. Since the moon’s orbit is not a perfect circular movement, the angle of subtension can vary a little but not too much.

This can be easily visualized if you hold your thumb out with your arm stretched, making a full round of the moon. This is because the thumb will subtend a larger angle than your eyes, even at a distance of about 380,000 km.

Sun

On the other hand, the sun will subtend an angle of 0.52$^{\circ}$ to an observer on the surface of the earth. This strikes an alarming situation since it is almost the same as that of the moon. Now you know why during a solar eclipse, the sun is almost fully covered by the moon.

So this proves that the object that is closer to the eyes will subtend a larger angle than the object that is farther away.

Because both the sun and moon subtend almost at a similar angle, the tiny moon covers up the gigantic sun, despite a huge size difference between the two. The glowing ring formed during the eclipse is due to the glowing gases.

The sun is about 3 times away from the earth as compared to the moon.

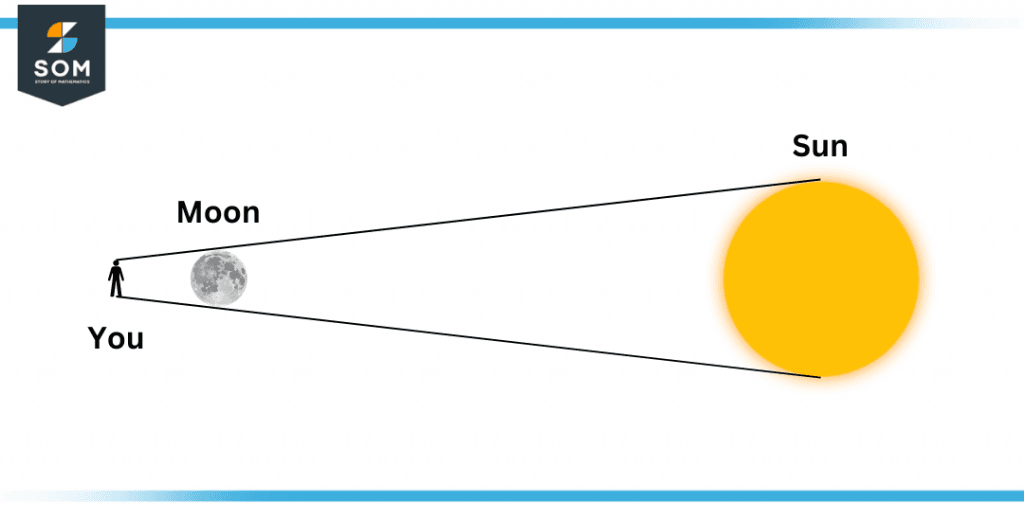
Figure 4 – A visual representation of a solar eclipse

Solved Examples of Subtended Angles

Example 1

Find x in the following figure.

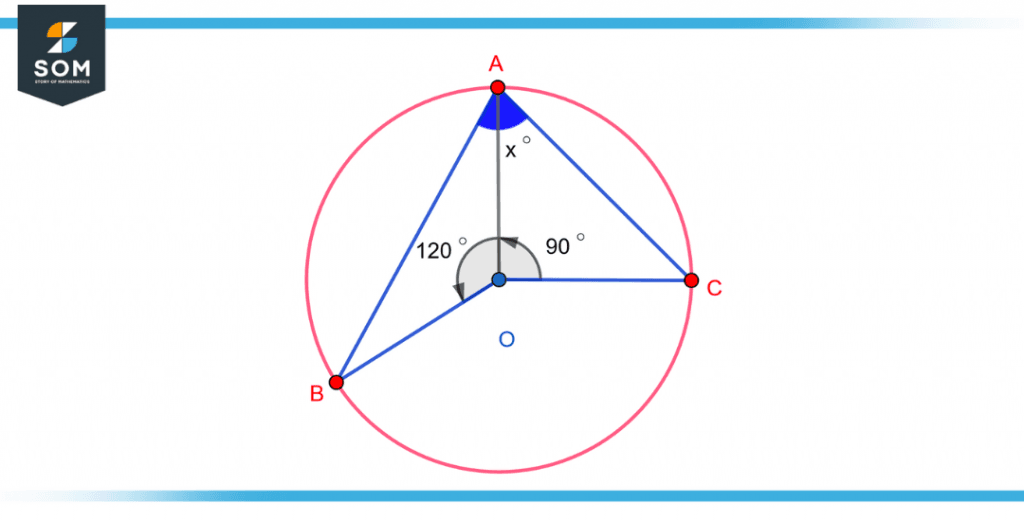
Figure 5 – Example 1 of the subtended angle at the center of a circle

Solution

The theorem states that:

$\angle$BOC = 2 x $\angle$BAC     ……. (1)

$\angle$BOC = 2x

$\angle$BOC + $\angle$BOA + $\angle$AOC = 360$^{\circ}$

$\angle$BOC + 120 + 90 = 360

$\angle$BOC + 210 = 360

$\angle$BOC = 360-210

$\angle$BOC = 150$^{\circ}$

Now finding the value of $\angle$BAC, which will result in the value of x.

From (1)

$\angle$BOC = 2 x $\angle$BAC

150 = 2$\angle$BAC

$\angle$BAC = 150 / 2

$\angle$BAC = 75$^{\circ}$

So the x comes out to be 75$^{\circ}$

Example 2

Find the value of x.

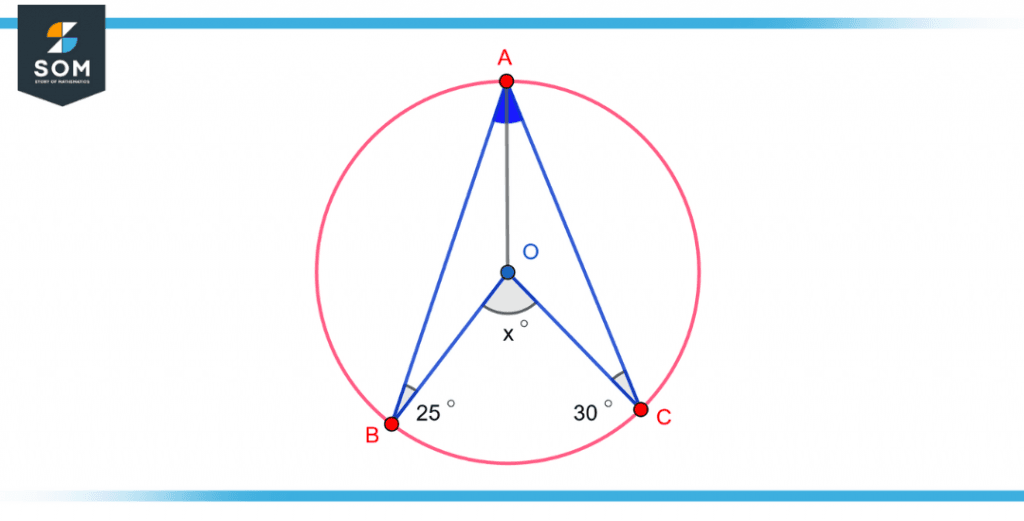
Figure 6 – Example 2 of the subtended angle at the center of a circle

Solution

Since,

OA = OB = OC (all are radii of the circle)

$\angle$OCA = $\angle$OAC = 30$^{\circ}$

$\angle$OBA = $\angle$OAB = 25$^{\circ}$

$\angle$BOC = 2 $\angle$BAC

$\angle$BAC = $\angle$BOA + $\angle$OAC

 = 25 + 30

 = 55$^{\circ}$

So,

$\angle$BOC = 2 x 55$^{\circ}$ = 110$^{\circ}$

So y is equal to 110$^{\circ}$.

All images are created using GeoGebra.

Substitution Definition < Glossary Index > Subtraction Definition