Subtraction|Definition & Meaning

The operation of subtraction is used to calculate the difference between two integers. If you have an object group and remove a couple of them, the object group gets smaller. For instance, your guests consumed 7 of the 9 cupcakes you purchased for your birthday celebration. You are now down to two cupcakes. 

Subtraction on the Real Line

Subtraction of integers can be performed on real lines illustrated in figure 1.

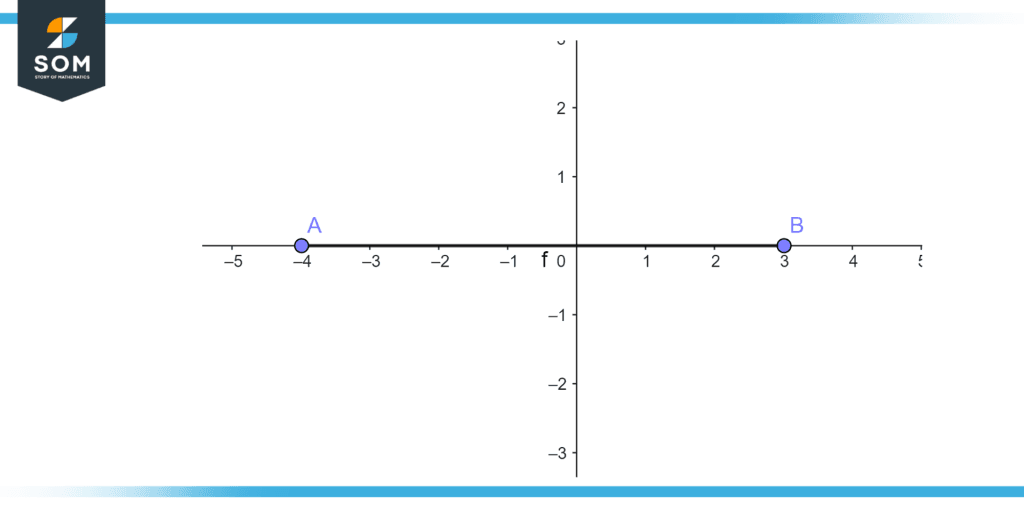
Figure 1 – Subtraction on real line

This may be expressed as a subtraction formula: 9 – 7 = 2, which means “nine less seven equals two.” The result of subtracting 7 from 9 is 2, or (9 – 7) Here, we divided two integers, 9, and 7, by one another to get the difference of 2.

About similar operations like addition and multiplication, subtraction also abides by predictable principles. It is possible to demonstrate each of these laws, starting with the subtraction of integers and expanding to real numbers and beyond. Abstract algebra investigates these patterns in general binary operations.

One of the easiest numerical operations is to subtract natural numbers. Young children can do extremely small-number subtraction. For instance, in elementary school, pupils are taught to subtract decimal numbers, beginning with single digits and working their way up to more challenging tasks.

An equation containing subtraction, such as A B, is typically considered as a shorthand notation for the addition A + (B), both in advanced algebra and computer algebra. As a result, A + B has two terms, A + B. Associativity and commutativity are now easy to employ.

Formula of Subtraction

Some terms from the subtraction expression are utilized when subtracting two numbers:

• Minuend: The number that is deducted to get the other number.
• The amount that has to be deducted from the minuend is known as a subtrahend.
• Difference: The outcome obtained by deducting the subtract from the minimum.

The formula for subtraction is Minuend – Subtrahend

Subtraction Symbol

In mathematics, there are several symbols. One of the crucial arithmetic symbols we employ while subtracting is the subtraction symbol. In the section above, we learned how to combine the numbers 9 and 7. The sign (-) joins the two integers and completes the supplied phrase when we notice the subtraction (9 – 7 = 2). The negative sign is another name for this symbol.

If we have to subtract 3 from 4 then we have to take 4 jumps to the left the answer is equal to -1 as illustrated in figure 2.

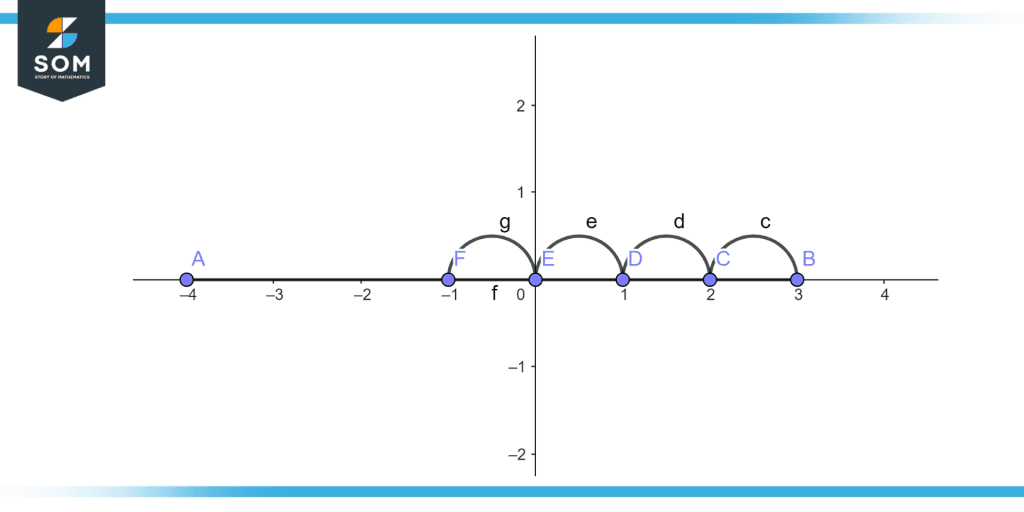
Figure 2 – Method of subtraction using real line.

Subtraction of Natural Numbers

Natural number subtraction is not closed: unless the minuend is greater than or equal to the subtrahend, the difference is not a natural number. For instance, subtracting 26 from 11 does not result in a natural number. One of two strategies is used in this situation:

• Conclude on that 26 cannot be subtracted from 11; otherwise, subtraction would only be a partial function.
• Answering as an integer that represents a negative number, the outcome of taking away 26 from 11 is -15.

Subtraction of Real Numbers

Only the addition and multiplication operations in combination with the unary operations that produce the additive and multiplicative inverses may be used to define the field of real numbers. The addition of the minuend and the additive inverse of the subtrahend may then be used to define the subtraction of one real number (the subtrahend) from another (the minuend).

Properties of Subtraction

Following are the properties of subtraction

Anti-commutative

Because subtraction is anti-commutative, the result is the opposite of the original result if the terms in a difference are reversed from left to right. Symbolically, if any two integers a and b are, then

a − b = −(b – a)

Non-associative

When attempting to define repeated subtraction, the fact that subtraction is non-associative becomes apparent. Generally speaking, the definition of “a b c” is either (a- b)- c or a-(b-c), however, these two definitions provide different results. To answer this problem, one must decide on a sequence of operations, with various orders leading to various outcomes.

Predecessor

For every integer a, the integer (a-1) is the greatest smaller than a, often known as the precursor of a, and it plays a specific function in the context of integers.

Teaching Subtraction in Different Regions

Various approaches are utilized to educate elementary school students about subtraction at different eras and in different countries. In what is referred to as traditional mathematics in the US, students are taught a specific procedure at the end of the first year (or during the second year) for use with multi-digit whole numbers. This procedure is then extended in either the fourth or fifth grade to include decimal representations of fractional numbers.

American Method

In almost all-American schools, subtraction is presently taught via crutch markers, borrowing, or regrouping (the decomposition procedure). The usage of crutches in American schools increased after William A. Brownell released research that claimed that crutches were advantageous to pupils utilizing this strategy, even though a way of borrowing had previously been recognized and published in textbooks.

The other subtraction techniques being used in America at the time were quickly replaced by this procedure as it gained popularity.

European Method

The European technique, sometimes known as the addition method, is a form of subtraction used in several European schools. This approach does not involve borrowing. There are also crutches, which differ by nation and are markers that help with remembering.

Solved Problems With Subtraction

Example 1

Subtract five with six using the real line.

Solution

Draw a real line from -five to five. Then, as we want to subtract five from six, we have to take six steps to the left from five, which is equal to a negative one. This is illustrated in Figure 3.

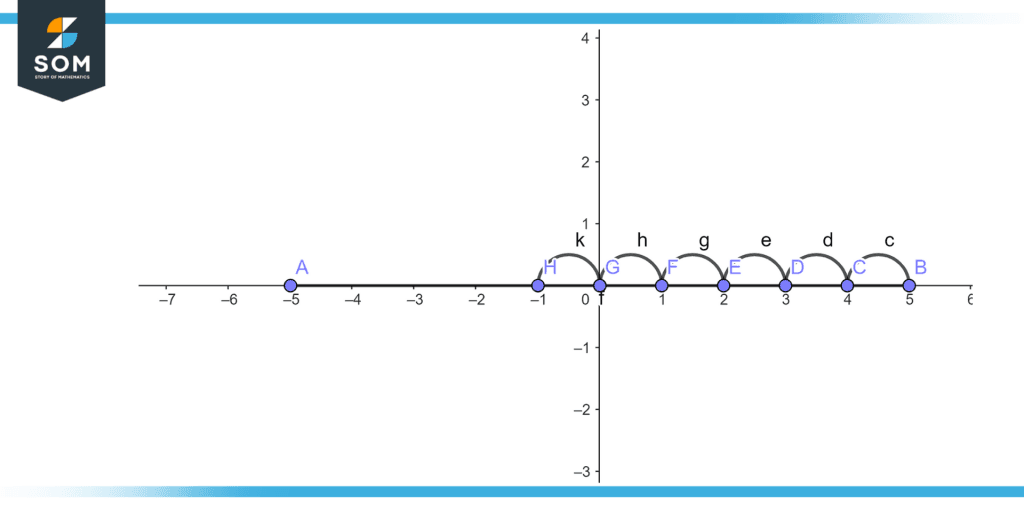
Figure 3 – Subtraction of two real numbers.

Example 2

Subtract 704 from 512 using the American method

Solution

We have to start subtraction from the right side, so four minus two equals two. As zero cannot be subtracted from one, we borrow one from seven, so ten minus one will be nine, and at last, six minus five will be equal to one.

 7  0  4     Minuend

-5  1  2     Subtrahend

 1  9  2     Rest or Difference

All images/mathematical drawings were created with GeoGebra.

Subtended Angle Definition < Glossary Index > Subtrahend Definition