Subtrahend|Definition & Meaning

What Is Subtrahend? 

The term “subtrahend” refers to the component of a subtraction, while “subtraction” refers to the mathematical process. Mathematically speaking, subtracting objects from an array is referred to as the elimination of those objects. The sign for subtraction is a negative sign, which looks like a dash.

For instance, there are 5-2 apples, which denotes that there were originally 5 apples, but now only 3 remain after having 2 removed. As a direct result, the gap between the numbers 5 and 2 is 3, also written as 5 2 = 3. In mathematics, the operation of subtraction is most often associated with natural numbers.

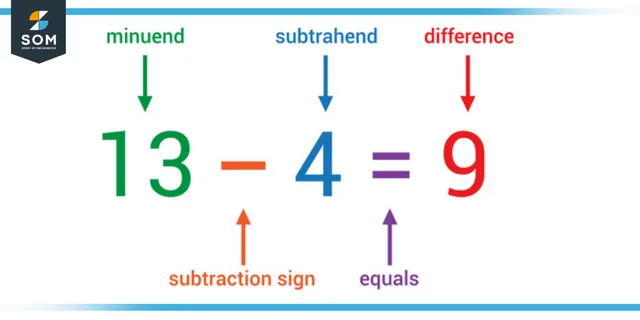
Figure 1: Representation of subtrahend.

The number, when subtracted from another number in an arithmetic operation, is referred to as the subtraction’s subtrahend, and it is defined as the number being subtracted. The term “difference” refers to the result obtained after “subtraction subtrahend” is applied to one number and “minuend subtrahend” to the other number used in operation.

Add, subtract, and multiply are the three components of mathematical operations.

minuend – subtrahend = difference

In the following illustration, 5 plus 2 equals 3.

The number 5 is known as the minuend, the number 2 is known as the subtrahend, and the number 3 is known as the difference.

The value of the subtrahend, the minuend, or the difference will be negative. The sign of the difference is determined by the minimum and maximum values of the difference, which is consistent with the arithmetic properties that are described below:

3 + 5= 8 (the sign of two positive numbers is positive) (the sign of two positive numbers is positive)

3 + -5= -2 ( symbol of more significant number) (the sign of more significant number)

-3 + 5= 2 ( symbol of more significant number) (the sign of more significant number)

-3 added to itself equals 6 (the sign of two negative numbers is considered “positive”).

Properties of Subtrahend

The process of subtraction can be broken down into numerous separate patterns. Because it is anticommutative, shifting the sequence of the steps will result in a different symbol for the answer. It’s also not associative, which means that when you subtract more than two integers, the order in which you do it makes a difference.

This is because the order in which the numbers are subtracted is essential. Since it is the adding identity, a number is unaffected if 0 is subtracted.

Regarding addition and multiplication, subtraction behaves predictably according to established norms. It is possible to demonstrate several of these rules, beginning with the subtraction of integers and moving on to real numbers and even further. Research into universal binary operations that adhere to these patterns is conducted using abstract algebra.

One of the most fundamental mathematical operations is called subtraction, and it’s used to take away natural numbers.

In advanced algebra and computer algebra, it is common to practice treating an equation requiring subtraction as a shorthand notation for the addition of A + (B). One example would be the expression A B. As a consequence, A B is composed of two separate terms: A and B. Now, associativity and commutativity can be utilized more successfully than ever before.

Figure 2: Representation of additive identity property.

Subtrahend Representation

The notation for subtraction, known as infix notation, places the minus sign (“-“) between each word in the expression. To express the conclusion, an equals sign is typically used. As an illustration, the expression “four minus three equals to one” (which is pronounced as “four minus three equals to one”)

The expression “nine minus three equals six” is interpreted as “nine minus three equals six.”

The equation reads “four minus one equals three,” and its pronunciation is “four one one equals three.”

There are also circumstances in which the concept of subtraction can be “understood” even the without a symbol.

In most cases, if there are two numbers in a column and the lower number is highlighted in red, this indicates that the higher number in the column should be subtracted from the lower number in the column, and the difference should be placed below, under a line. The accounting industry is the one that uses this most frequently.

Missing Subtrahend Method

It is the most common method that teachers use to check their student’s knowledge of the fundamental concepts behind the arithmetic operators they teach. This method is intended for the students. Students are tasked with determining the value of the subtrahend, which is implied by the equation’s name but has yet to be explicitly stated.

In a phrase involving subtraction, if the value of the subtrahend is unknown, but the value of the minuend and the difference are known. The value of the subtrahend can be determined by subtracting the difference from the minuend. You may see an example of an equation with a missing subtrahend in the following:

For instance, the subtrahend of equation 70 -= 50 is 70 – 50=20.

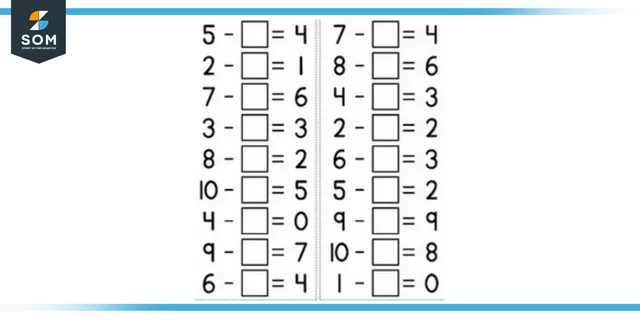
Figure 3: Missing subtrahend.

Complement Method

One of the ways to be utilized in the process of subtraction is known as the complement approach. The complement of one is zero, and the complement of zero is one. One is the complement of 0. In this approach, the value of the number is expressed as a decimal, composed of digits 0 and 1, respectively.

One approach for deducting one number from another is the complements method. This method involves adding only positive values.

Examples of Subtrahend

Example 1

Find the missing subtrahend in the following equation:

73 – x = 43

Solution

x = 73 – 43

x = 30

Example 2

Solved the following problem by finding the difference value:

25 – 90 = ?

Solution

25 – 90 = x

-65 = x

All images/graphs are created using GeoGebra.

Subtraction Definition < Glossary Index > Successive Definition