Successive|Definition & Meaning

In mathematics, successive means a sequence of values created in a particular order, typically via a mathematical procedure or algorithm. The sequence is generated by continually performing a mathematical function to a beginning value, yielding a new value with each iteration. 

The mathematical approach utilized to construct the sequence determines the ordering of the numbers. It is common practice to utilize successive integers to estimate solutions to issues that cannot be addressed exactly or to determine the maximum value or minimum value of a function.

Figure 1: Illustration of Successive Numbers

Successive Numbers and Numerical Analysis

It is common practice in numerical analysis to employ successive numbers to approximately solve issues that could not be solved precisely. Finding the roots of problems and resolving differential equations are two frequent uses of successive numbers in numerical analysis.

Finding Roots

Finding the roots of an integer is one of the most popular uses of successive values in numerical analysis. An equation’s root is a number that, when introduced into the equation, causes it to reach zero. For instance, the roots for the equation below will be x = 3 and x = -3.

f(x) = x² – 9 = 0

Numerical techniques like the bisection method, secant method, and Newton-Raphson method are frequently employed to discover approximations of equations’ roots because it is usually impossible to calculate the equation’s roots analytically. These techniques work by repeatedly performing mathematical computations on an initial estimate to get repeated estimations of the root.

Solving the Differential Equations

The solution of differential equations is yet another significant use of successive numbers in numerical analysis. Differential equations are mathematical expressions that explain how a phenomenon alters over time. They are employed in the modeling of a vast array of physical and biological processes. one popular approach for resolving differential equations is the Euler method. This method is focused on constructing successive estimations of the problems by repeatedly performing mathematical functions on a starting value.

Successive Numbers in Calculus

Numerous calculus operations, such as successive derivatives and integrals, make use of successive numbers.

Successive Derivatives

A function’s derivative in calculus is a measurement of how the function alters as its input alters.  The second derivatives, also referred to as the second-order derivatives, are derivatives of the first derivatives. In the same manner, the derivative of (n-1)^th order derivative is the n^th order derivative. They are often referred to as successive derivatives and are employed to examine the local behavior of a function close to a point.

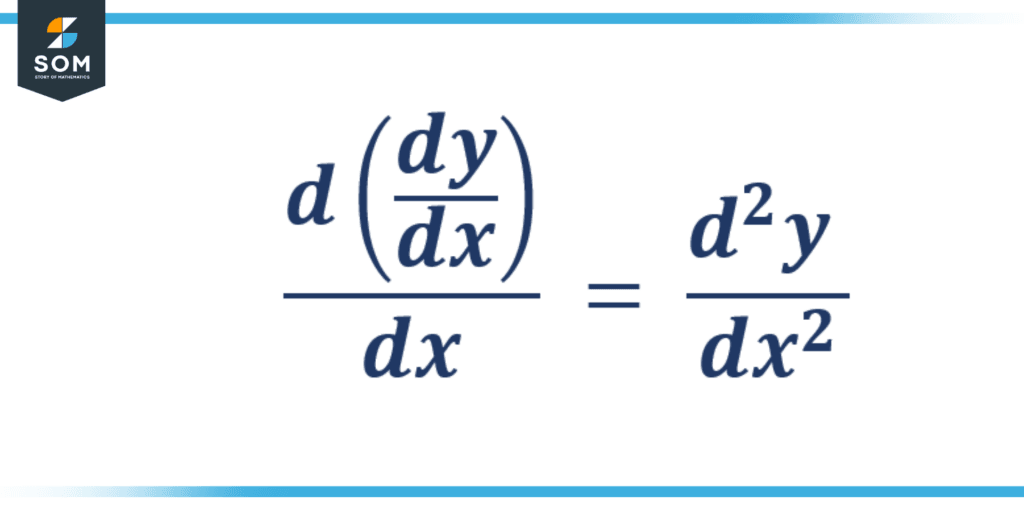
Figure 2: Illustration of Successive Derivatives

Successive Integrals

The integral of functions in calculus represents the region beneath the curve of the functions. The function whose derivative is the original function is known as the definite integral and is commonly referred to as the antiderivative. in the same manner, the n^th integral is the integral whose derivative is the (n-1)^th integral. These can be used to determine the overall variation in a function during a specific period of time and are often referred to as successive integrals.

Successive Numbers and Optimization

In the process of optimizing, we determine the maximum or minimum value of a function by using successive numbers. The process of determining which of a number of potential solutions is the most beneficial is known as optimization. In a variety of optimization methods, such as gradient descent, conjugate gradient, and Newton’s method, successive integers play an important role.

Minimizing and Maximizing Functions

When determining the minimum or maximum value of a function, successive numbers are considered. It is possible for the function to be quite straightforward, such as a quadratic function, or rather complicated, such as a neural network. Various optimization strategies, such as gradient descent, conjugate gradient, and Newton’s method, make use of subsequent integers to continuously improve an initial approximation of the least or maximum value.

Linear and Non-linear Optimisation

In both linear and non-linear optimization, successive numbers are essential. When it comes to optimization, linear optimization focuses on linear functions and limitations, while non-linear optimization focuses on non-linear functions and limitations. The non-linear optimization process is utilized in various domains, including control systems, image analysis, and computer vision.

Generation of Successive Numbers Using Iterative Techniques

In mathematics, the generation of successive numbers frequently makes use of a method called the iterative approach. Iterative approaches entail continually performing a mathematical operation to the original value, which ultimately results in a different value for each iteration of the process. The mathematical algorithm that was used to construct the series of numbers is what decides the order of the numbers within it.

There are a variety of iterative approaches that can be utilized, such as the following, to produce successive numbers:

1. Fixed-Point Iteration
2. Newton-Raphson Method
3. Successive Over-Relaxation
4. Jacobi and Gauss-Seidel method

Generation of Successive Numbers Using Recursive Methods

In mathematics, generating successive numbers can be accomplished through the application of recursive techniques. In recursive approaches, a sequence of numbers is defined in terms of the numbers that came before them in the sequence. This is often accomplished through the utilization of a recursive equation or algorithm.

There are a variety of recursive approaches that you can employ to produce successive numbers, such as the following:

Fibonacci Numbers

The famous Fibonacci numbers are an iconic illustration of a recursive sequence. Each successive number in the series represents the addition of the two numbers that came before it. The digits 0 and 1 mark the beginning of the sequence, and from that point on, each succeeding number in the series is calculated by adding the two numbers that came before it.

Recursive Algorithm

An algorithm is said to be recursive if it can invoke itself with data that is less complex. Computing the factorial of an integer, for instance, can be performed recursively.

Recursive Formulas

A formula is said to be recursive if it describes a sequence of numbers by making reference to the numbers that came before them in the sequence.

Generation of Successive Numbers Using Convergence Criteria

The application of convergence criteria allows one to ascertain whether or not a succession of successive numbers has, in fact, converged to a certain number or answer.

The criteria are employed to assess whether the sequence has acquired a level of stability, which is a state in which the values contained inside the sequence do not vary substantially from one iteration to the next.

For generating successive numbers, one can utilize any one of a number of distinct convergence criteria, such as the following:

Absolute Error Criteria

This criterion is determined by the absolute deviation that exists between the sequence’s two most recent values.  The sequence is deemed to have converged when the variation is smaller than a predetermined criterion for success.

Relative Error Criteria

This criterion is determined by examining the degree of dissimilarity that exists between the sequence’s two most recent values. It is determined that the sequence converges when the disparity is smaller than a particular threshold.

Ratio Test

This criterion evaluates how subsequent values in the sequence relate to one another in terms of their ratio. When the ratio gets close to a particular value, we say that the sequence has converged because it has reached that point.

Example of Successive Values

Complete the series of following successive values

1. 1, 3, 5, ?, 9, 11
2. Monday, Tuesday, Wednesday, ?, Friday, Saturday, and Sunday
3. 2, 4, 6, ?, 10, 12

Solution

In (a), we can clearly see that the series is of odd numbers. Thus, the completed series is as follows:

(a) 1, 3, 5, 7, 9, 11

In (b), we can clearly see that the series is on weekdays, so the completed series is as follows:

(b) Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday

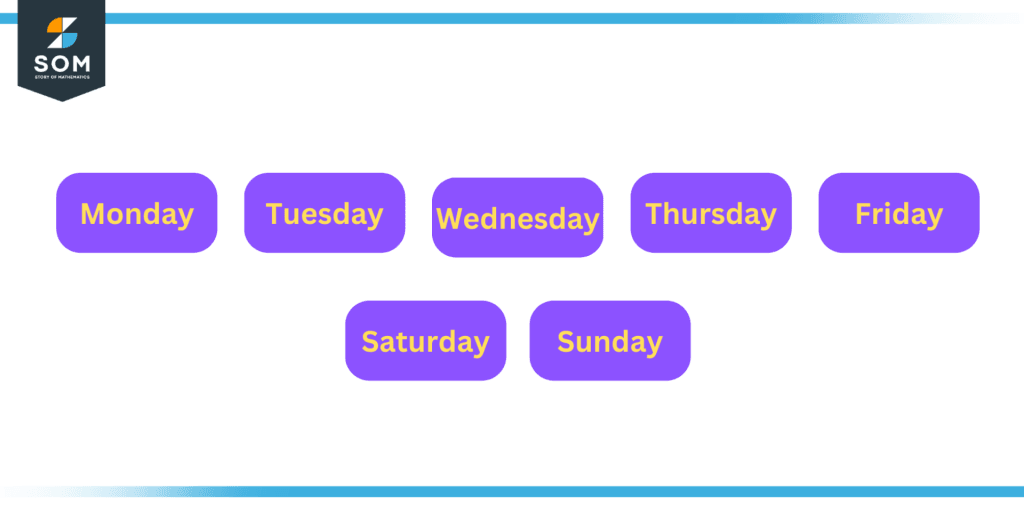
Figure 3: Illustration of Successive Weekdays

In (c), we can clearly see that the series is of even numbers, so the completed series is as follows:

(c) 2, 4, 6, 8, 10, 12

All images/mathematical drawings were created with GeoGebra.

Subtrahend Definition < Glossary Index > Sum Definition