JUMP TO TOPIC
Standard Notation|Definition & Meaning
Definition
The way we usually write a number, or the most common form of writing a number, is called standard notation. For example, we can write one thousand twelve hundred and thirty as 1230 (standard notation), 1 x 1000 + 2 x 100 + 3 x 10 + 0 x 0 (expanded notation), or 1.230 x 103 (scientific notation). In most cases, we will see it written as 1230.

Figure 1 – Overview of Standard Notation
In mathematics, standard notation is a widely used way to express numbers. It offers a clear and concise way to convey mathematical ideas and is used to represent both whole numbers and decimals.
Digits are used in standard notation to represent whole numbers. For instance, “15” is used to represent the number 15. A minus sign is placed next to negative numbers to indicate them. For instance, “-15” is the way to write the negative number -15.
A decimal point is used in standard notation to denote decimals. The decimal point separates the decimal’s whole number and fractional parts. For instance, “3.14” is the way to write the decimal number 3.14. “3” is the whole number portion, and “14” is the fractional portion.
In standard notation, exponents are used to represent extremely large or extremely small numbers. The exponent (or power) indicates how many times the base has been multiplied by itself. The exponent is written in superscript form after the base. For instance, 103 denotes the value of 10 multiplied by itself three times, or 1000. Similarly to that, 10-3 stands for 1/1000, or 0.001.
Motive Behind Writing a Number in Standard Notation
The main goals of using standard notation are to make mathematical concepts easier to understand and communicate, as well as to provide a clear and consistent way of expressing numbers in mathematics. The following are some advantages of using the standard notation:
- Clarity and accuracy: Standard notation offers a straightforward and unambiguous way to express numerical values and mathematical ideas, making it simpler to communicate mathematical ideas and prevent misunderstandings.
- Consistency: Mathematicians can more easily understand and collaborate with one another, no matter where they are in the world, by using a standardized way of expressing numbers and mathematical concepts.
- Usability: Standard notation is intended to be simple to use and comprehend, making it accessible to a wider range of people, including non-specialists and students.
- Flexibility: A wide range of numbers and mathematical ideas, from straightforward whole numbers to more intricate decimals and functions, can be expressed using standard notation.
- Convenience: By utilizing scientific notation and exponents, standard notation offers a compact and practical way to represent large or small numbers.
Standard Notation Vs Scientific Notation

Figure 2- Difference between Standard notation and Scientific notation
In mathematics, there are two ways to express numbers: standard notation and scientific notation. Here is a thorough contrast of the two.
- Representation: To express numbers in their usual form, standard notation is used. Scientific notation, on the other hand, is used to write extremely large or small numbers in a compact form.
- Form: A number is expressed in standard notation as a whole number or a decimal, with or without a negative sign. A number is written in scientific notation as a power of 10 times a number between 1 and 10.
- Precision: Standard notation offers a simple and accurate method of expressing numbers, but it can be difficult to use when expressing extremely large or tiny numbers. Such numbers can be expressed succinctly in scientific notation, but it may not be as accurate as standard notation.
- Usability: Standard notation is simple to read and understand for the majority of numbers, but as the numbers get bigger or smaller, it becomes more challenging. On the other hand, scientific notation offers a condensed and practical way to represent large or small numbers, making it simpler to work with such numbers.
- Accuracy: When expressing numbers, both standard notation and scientific notation are equally accurate. The right number of significant figures must be used in scientific notation, though, so care must be taken.
- Range of numbers: Any number can be expressed using standard notation, but very large or very small numbers make it difficult to use. The scientific notation may not be appropriate for expressing numbers in the middle range because it is specifically intended to express very large or very small numbers.
Converting From Scientific Notation to Standard Notation
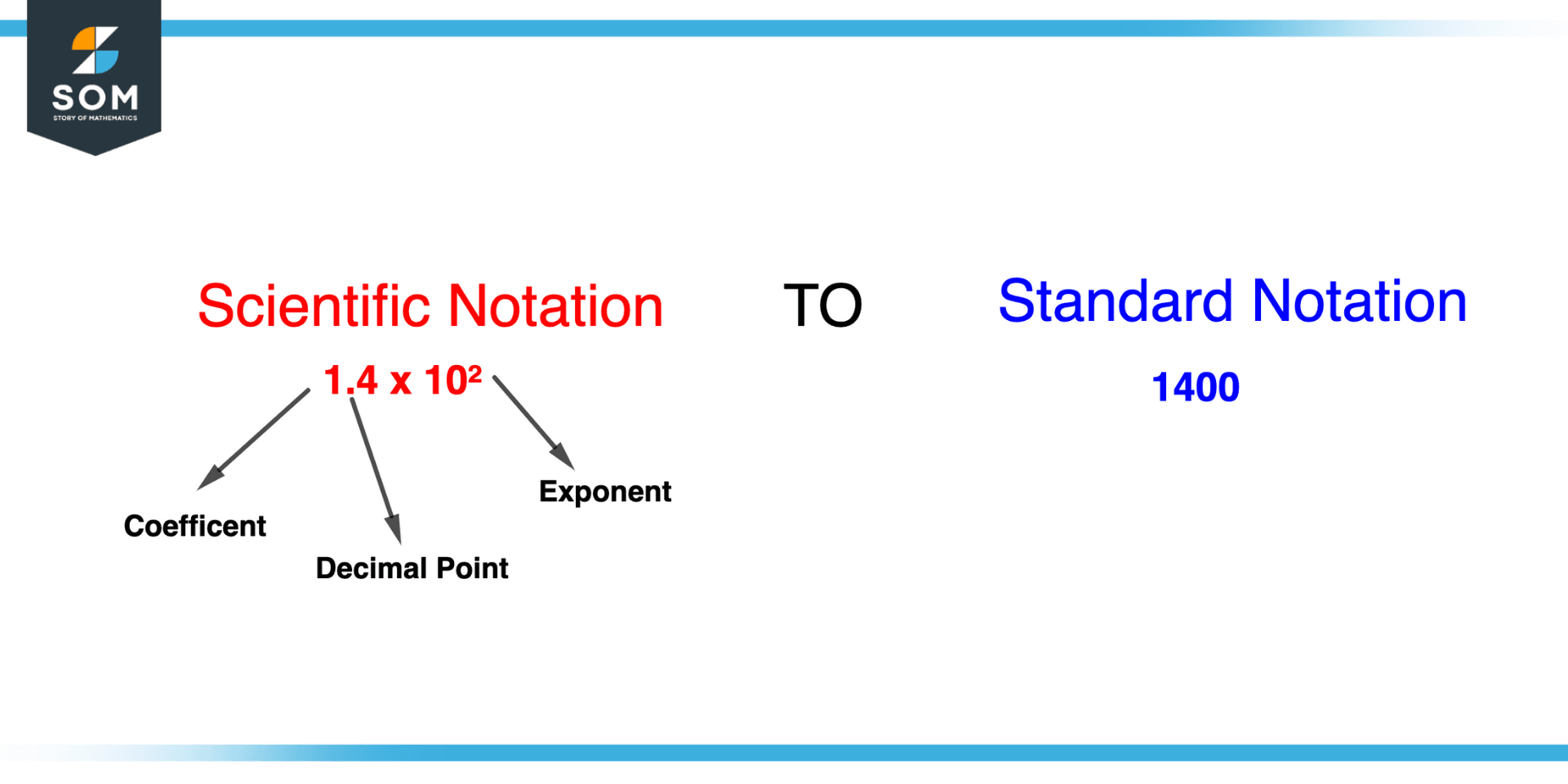
Figure 3 – Conversion of Scientific Notation to Standard Notation
Observe these steps to translate a number from scientific to standard notation:
- Find the coefficient. The coefficient is the number that appears to the left of the scientific notation symbol “x 10”.
- Find the exponent. It is the number that follows “x 10” in the scientific notation expression.
- Place the decimal point in the coefficient. If the power is positive, the decimal point should be shifted to the right by the exponent’s specified number of places. If the power is negative instead, the decimal point should be shifted left by the exponent’s specified number of places.
- Write the number in standard notation, with the decimal point in the proper location and any additional trailing zeros as needed.
Solved Examples Emphasizing the Concept of Standard Notation
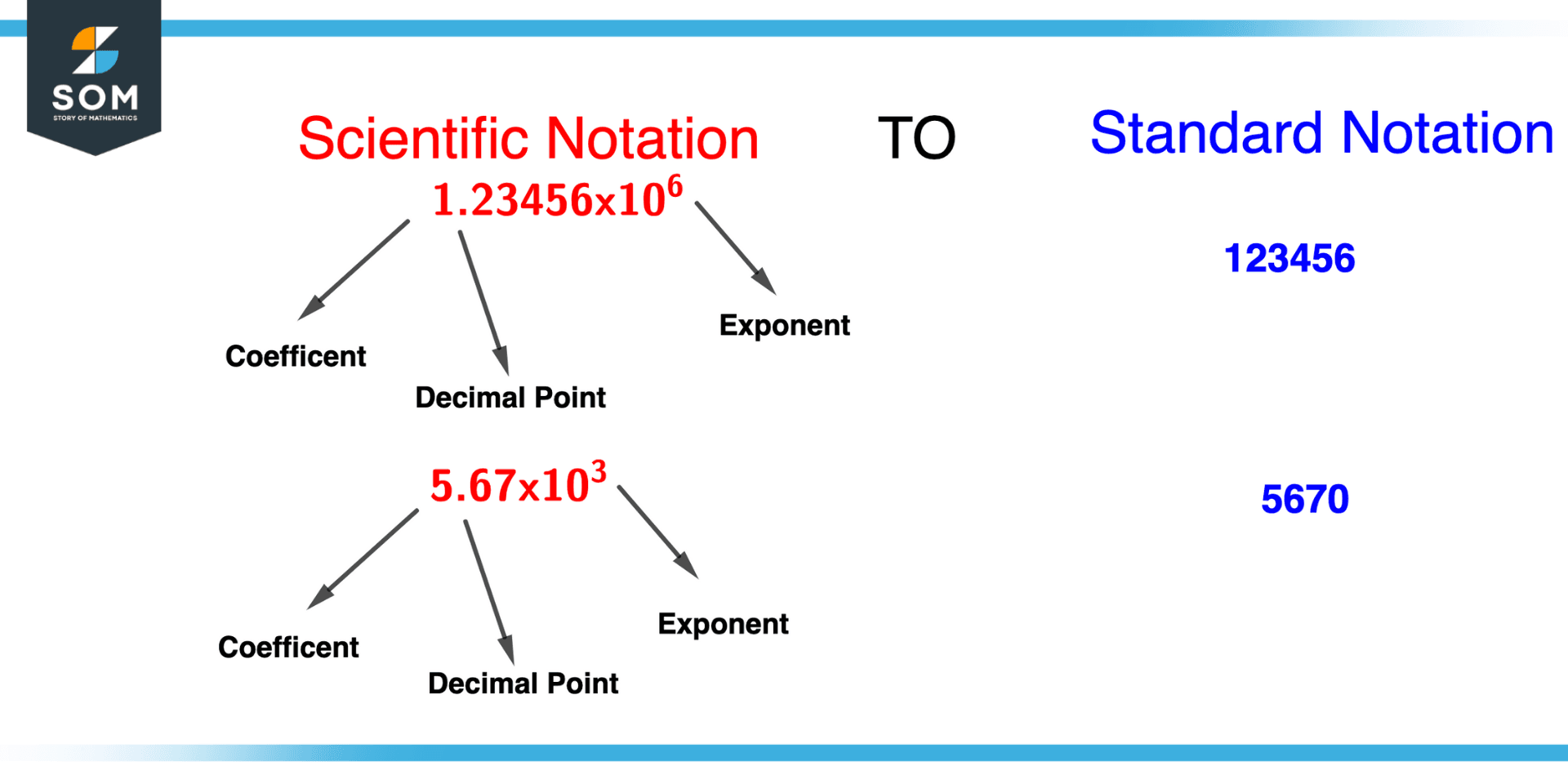
Figure 4 – Standard Notation Example
Example 1
Convert the number 1.23456 x 106 into standard notation.
Solution
1. Find the coefficient.
In this case, the value is 1.23456.
2. Find the exponent.
in this case which is 6.
3. Put a decimal point.
Add six places to the right of the decimal point to get 123456.
4. Write the number in standard notation.
The standard notation for the number is 123456.
Be aware that it’s crucial to use the appropriate number of significant figures when converting numbers from scientific to standard notation.
Example 2
Convert 5.67 x 103 to standard notation.
Solution
1. Find the coefficient.
The coefficient in this instance is 5.67.
2. Find the exponent.
in this case which is 3.
3. Put a decimal point.
5670 after moving the decimal point three places to the right.
4. Write the number in standard notation.
The standard notation for the number is 5670.
Consequently, 5670 is equal to 5.67 x 103 in standard notation.
All mathematical drawings and images were created with GeoGebra.
