JUMP TO TOPIC
Velocity|Definition & Meaning
Definition
Velocity is a quantity that defines two things: the direction of an object’s movement and how fast it moves (i.e., its speed). Quantities like this are called vector quantities, as they specify both magnitude (value) and direction. So, if a car is moving along a North-facing highway at 60 mph, then “60 mph Northwards” is velocity, while “60 mph” is just its speed.
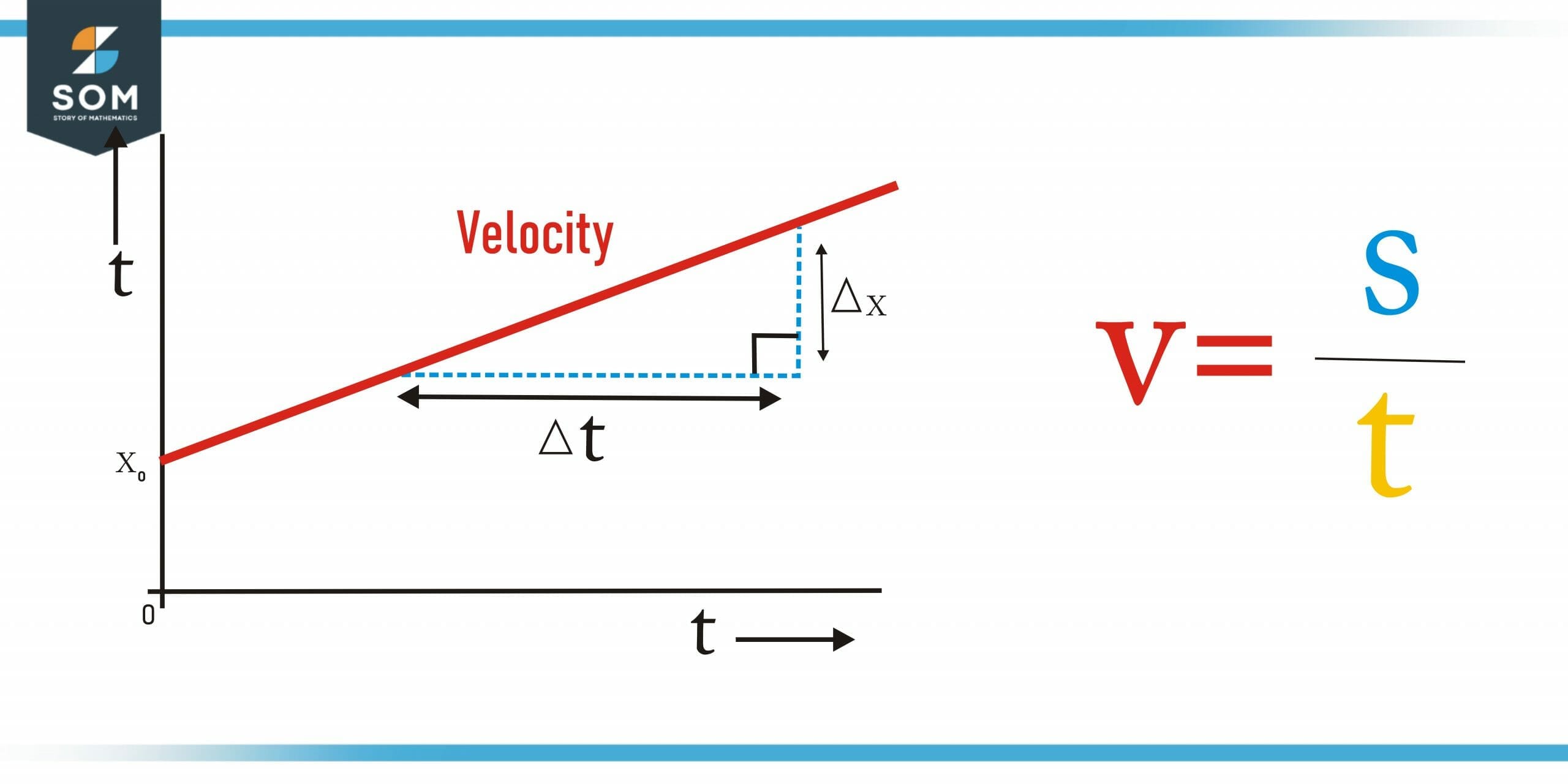
Figure 1 – Graphical Representation of Velocity and its basic formula
Types of Velocity
There are two types of velocity: average velocity and instantaneous velocity. The total change in position i.e displacement of an object is a known period of time divided by the interval of time and is known as the average velocity of that object. It is represented by the formula:
average velocity = (final position – initial position) / time interval
For example, if a car travels from point A to point B in 10 minutes and covers a distance of 50 kilometers, its average velocity would be 5 km/min.
On the other hand, if the velocity of an object is calculated at an instant or particular point in time this is known as instantaneous velocity. It is represented by the formula:
instantaneous velocity = (change in position) / (change in time)
Difference Between Average and Instantaneous Velocity
There is one major difference between both of these velocities in average velocity entire time interval is taken and for instantaneous velocity, the velocity is taken at a specific instant or point of time.
An object’s velocity can change due to various factors, such as acceleration (a change in the rate of change in velocity), deceleration (a decrease in velocity), or a change in direction. For example, a car that is accelerating from a stop will have a higher velocity as it moves forward, while a car that is braking or turning will have a lower velocity.
Factors Affecting the Velocity
Several factors can affect an object’s velocity, including its mass, the force applied to it, and the resistance it encounters. For example, a heavier object will require more force to achieve the same velocity as a lighter object, and an object moving through a denser medium (such as water) will experience more resistance and therefore have a lower velocity than the same object moving through a less dense medium (such as air).
In physics, velocity is often used in conjunction with other concepts such as displacement, acceleration, and momentum. Displacement is the change in the position of an object, while the rate of change of velocity of an object over some time is known as acceleration. Momentum is the product of an object’s mass and velocity and is a measure of the object’s “inertial mass,” or its resistance to changes in its state of motion.

Figure 2 – A train moving with velocity v
Applications of Velocity
Velocity is an important concept in a variety of fields, including engineering, transportation, and sports. In engineering, velocity is used to calculate the force required to move an object, as well as the power needed to overcome resistance.
In transportation, velocity is used to determine the time it takes to travel from one point to another and to calculate fuel efficiency. In sports, velocity is used to measure the speed of a pitch in baseball, or the speed of a shot in soccer or hockey.
So, velocity is a measure of the rate at which an object changes its position, and is a crucial concept in fields such as engineering, transportation, and sports. It can be expressed as either average velocity, which takes into account the entire journey of an object, or instantaneous velocity, which measures the velocity at a specific point in time.
Factors that can affect an object’s velocity include its mass, the force applied to it, and the resistance it encounters.
Real-life Solved Examples
Example 1 – Calculating the Average Velocity Between Two Points
A car travels from one city to another. Ler initial point is A and the final point is B and takes 20 mins to reach the destination i.e B, covering a distance of 100 kilometers. What is the average velocity of the car?
Figure 3 – A car moving from point A to point B
Solution
To calculate the average velocity of the car we will use the following formula:
average velocity = (final position – initial position) / time interval
In this case, the initial position is point A, the final place is point B, and the time interval is 20 minutes.
Plugging these values into the formula gives us:
average velocity = (100 km – 0 km) / (20 min)
= 5 km/min
Example 2 – Calculating Velocity in Miles per Second
An airplane travels from New York to Los Angeles in 6 hours, covering a distance of 3,000 miles. What is the average velocity of the airplane in miles per hour?
Solution
First, we need to convert the time interval from hours to minutes. There are 60 minutes in 1 hour, so:
6 hours = 6 * 60 = 360 minutes
Then, we can use the formula for average velocity to calculate the average velocity of the airplane:
average velocity = (final position – initial position) / time interval:
= (3000 miles – 0 miles) / (360 min)
= 8.33 miles/min
To express the velocity in miles per hour, we need to convert the velocity from minutes to hours. There are 60 minutes in 1 hour, so
8.33 miles/min = 8.33 * (1 hour / 60 min)
= 8.33 / 60 = 0.138 hours/mile.
Finally, we can convert the velocity to miles per hour by flipping the fraction:
= (1 mile) / (0.138 hours/mile)
= 7.25 miles/hour
Example 3 – Calculating the Velocity of a Marathon Runner
A runner completes a marathon in 4 hours, covering a distance of 26.2 miles. What is the average velocity of the runner in miles per hour?
Solution
First, we need to convert the time interval from hours to minutes.
There are 60 minutes in 1 hour, so:
4 hours = 4 * 60 = 240 minutes.
Then, we can use the formula for average velocity to calculate the average velocity of the runner:
average velocity = (final position – initial position) / time interval
= (26.2 miles – 0 miles) / (240 min)
= 0.109 miles/min
To express the velocity in miles per hour, we need to convert the velocity from minutes to hours.
There are 60 minutes in 1 hour:
so 0.109 miles/min = 0.109 * (1 hour / 60 min)
= 0.109 / 60
= 0.00182 hours/mile.
Finally, we can convert the velocity to miles per hour by flipping the fraction:
= (1 mile) / (0.00182 hours/mile)
= 547.8 miles/hour
All mathematical images are generated using GeoGebra.
