Vertex (Parabola)|Definition & Meaning

Types of Parabolas in the Context of Vertex

There are four varieties of parabolas in relation to the vertex: 

Upward Opening

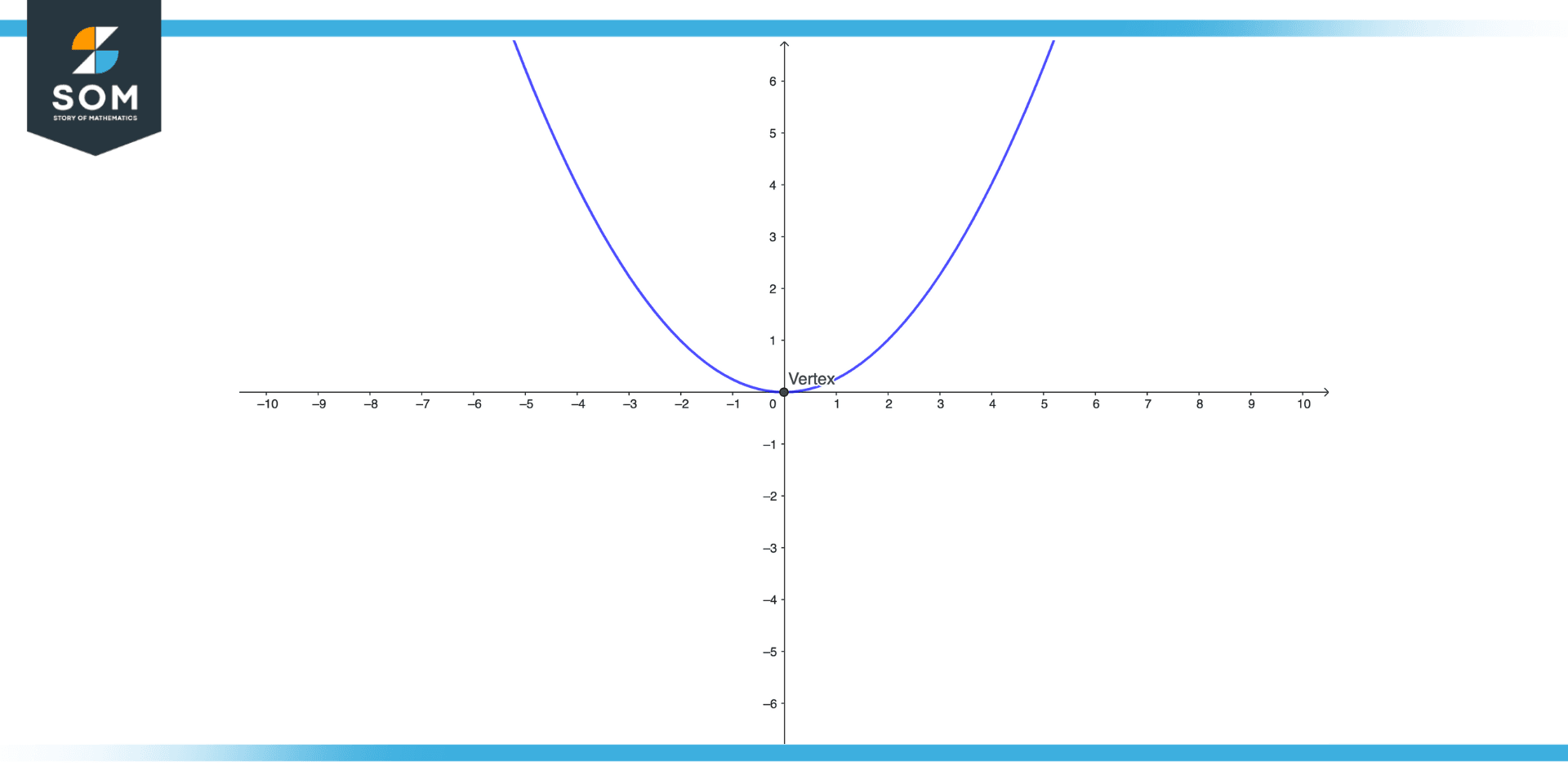
Figure 1 – Figure showing Upward Opening Parabola

A parabola that opens upwards and has its vertex at the bottom of the curve is referred to as an upward-opening parabola. A minimum point is the vertex of a parabola that opens upward.

Downward Opening

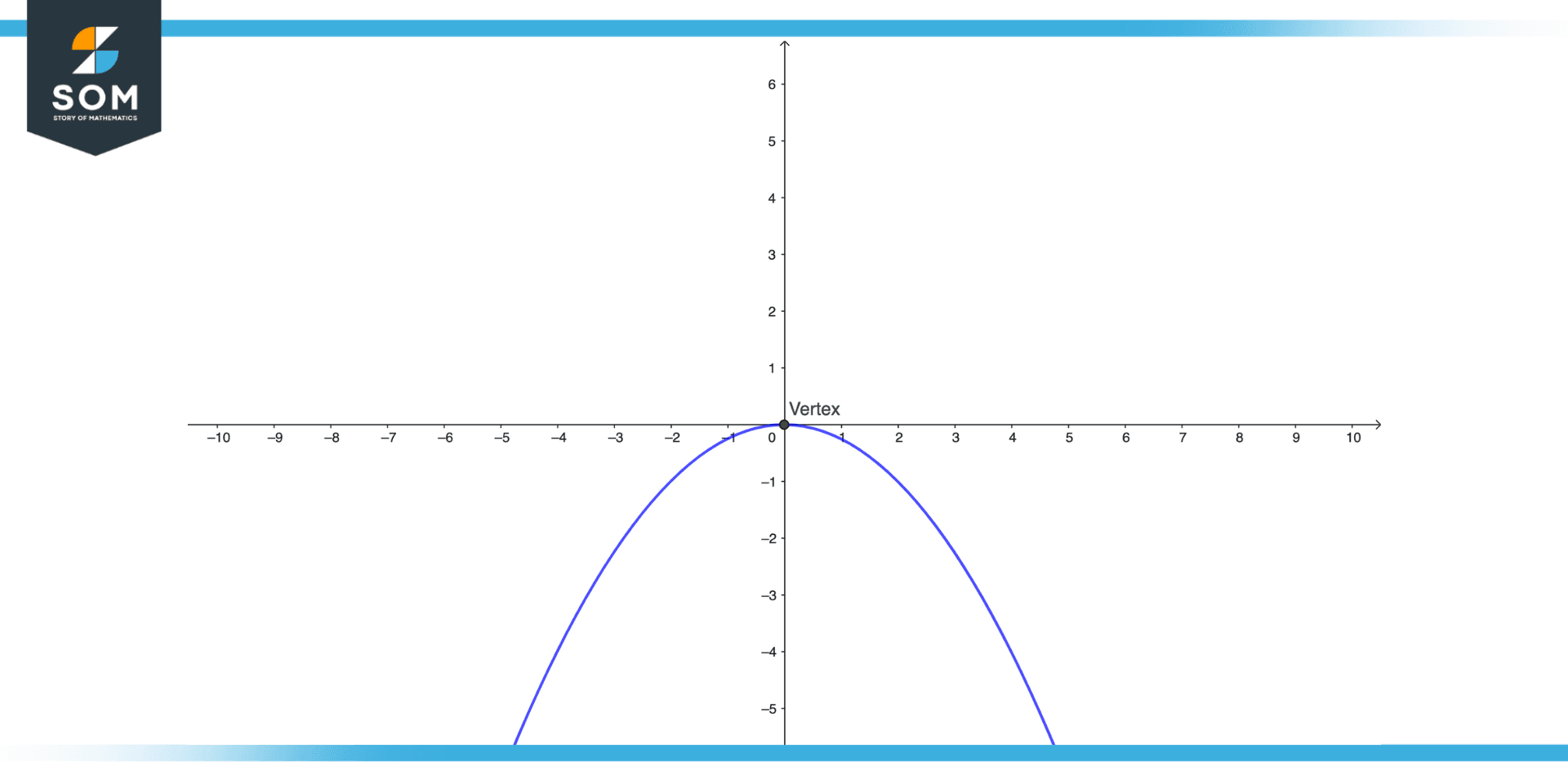
Figure 2 – Illustration of a parabola opening downward

A downward-opening parabola is a parabolic curve with its vertex at the highest point of the curve and an opening that is downward. A downward-opening parabola’s vertex is its highest point.

Left Opening

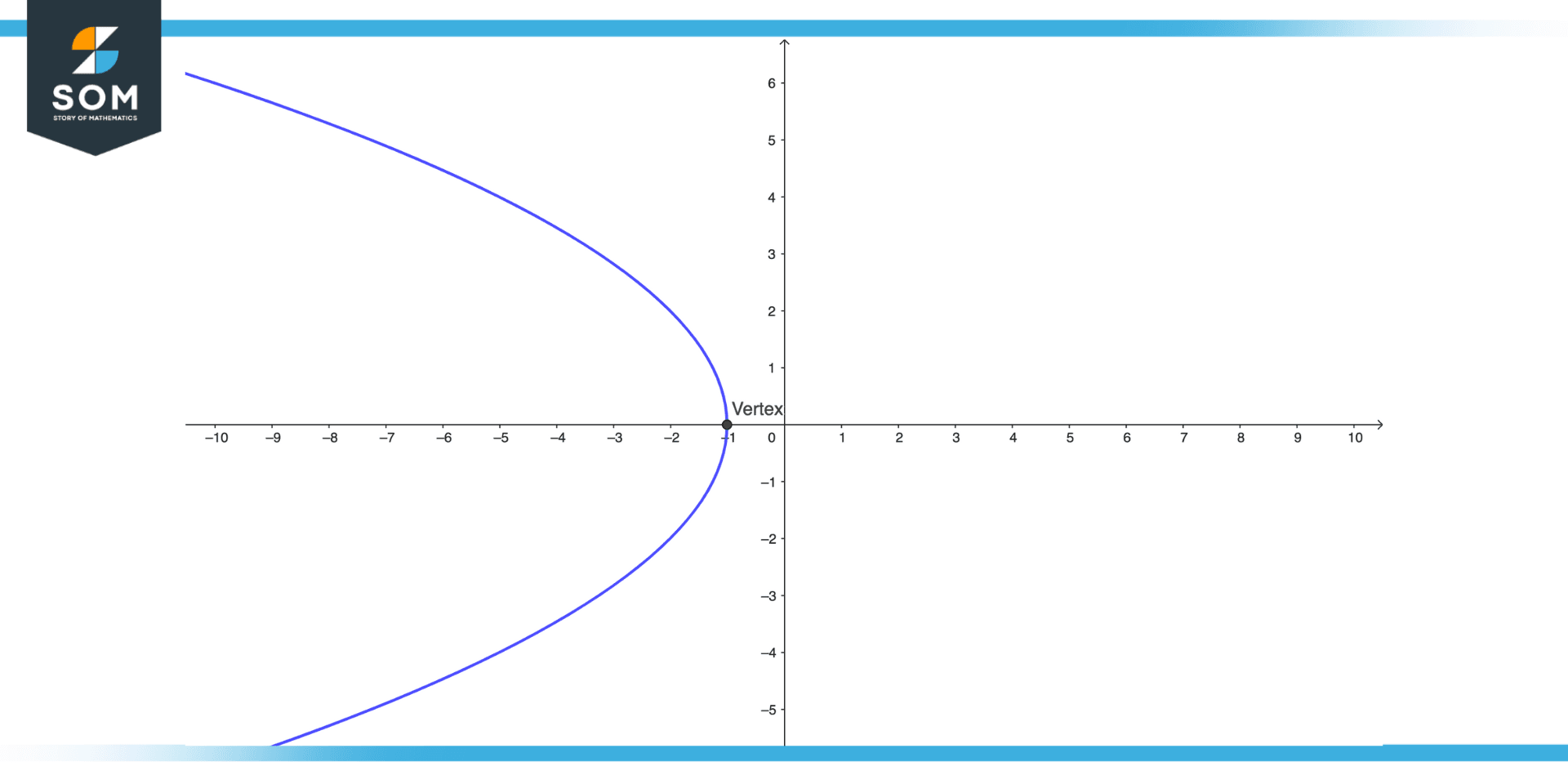
Figure 3 –  A Left Opening Parabola

A left-opening parabola is a parabolic curve with its vertex on the right side of the curve and an opening to the left.

Right Opening

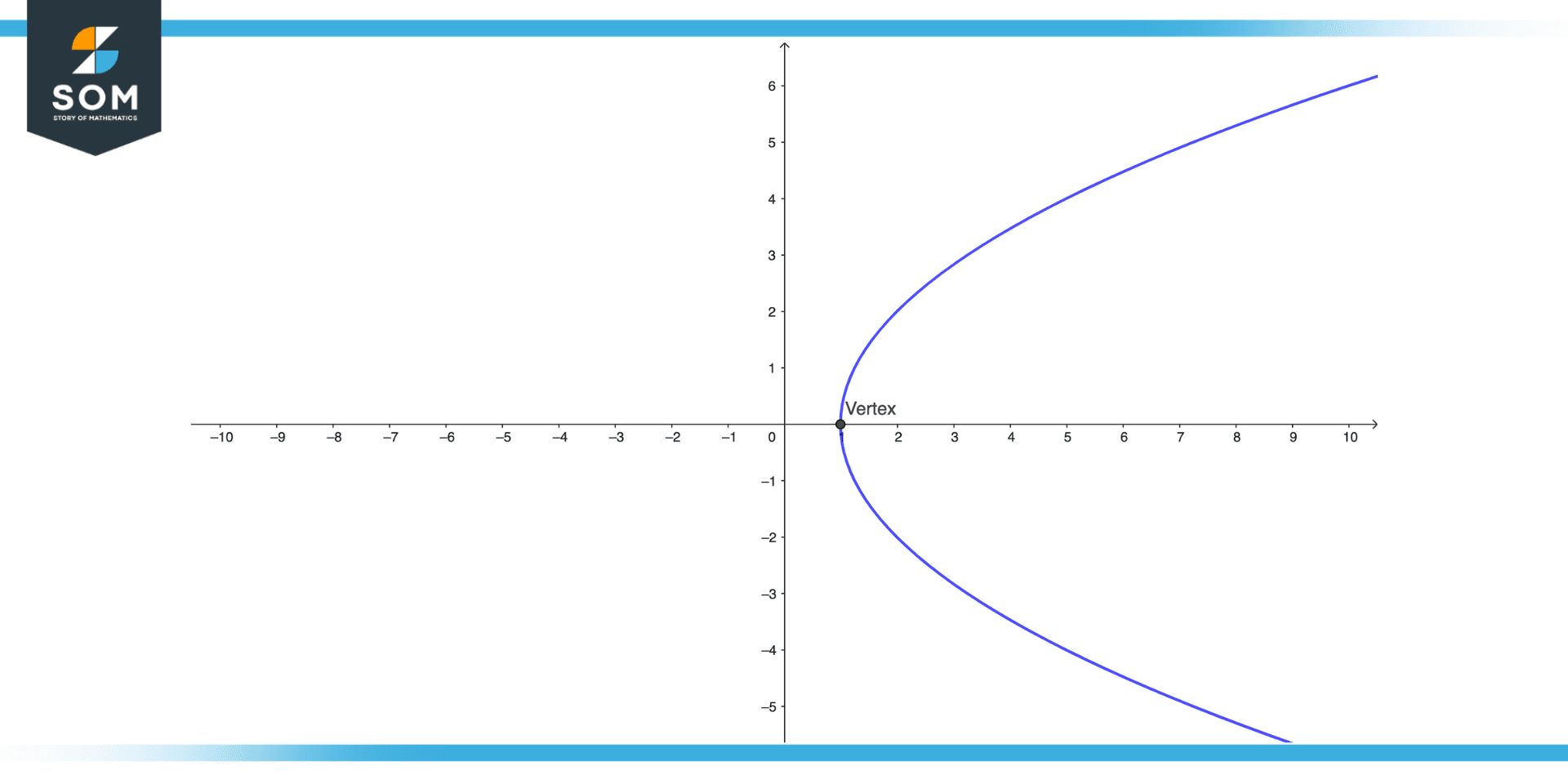
Figure 4 – Visualization of parabola opening right

A right-opening parabola is a parabolic curve with its vertex on the curve’s left side and an opening to the right.

Methods To Find Vertex of Parabola

The geometric method and the algebraic method can both be used to locate the vertex of a parabola.

Algebraic Approach

The equation of a parabola is used to determine its vertex using algebra. The formula y = ax² + bx + c, where a, b, and c are constants, represents a parabolic equation. The vertex’s x-coordinate can be determined by applying the formula x = -b/(2a), and the y-coordinate can be obtained by adding this quantity to the parabola’s equation.

Geometric Approach

Graphing the parabolic equation is required to determine a parabola’s vertex geometrically. Draw a line parallel to the parabola’s axis of symmetry that crosses the curve at the vertex in order to determine the vertex. The vertical line that cuts through the vertex and divides the parabolic curve into two equal parts is known as the axis of symmetry.

Properties of Vertex of Parabola

A parabola’s vertex has the following characteristics:

• Location: Depending on whether the parabola opens upwards or downwards, the vertex is situated at either the highest or lowest point of the parabolic graph.
• Symmetrical: A parabola is symmetrical about its vertex, which means that if you fold it in half along the vertex, the two halves will line up exactly.
• Axis of symmetry: The axis of symmetry is the line that traverses the vertex and is perpendicular to the directrix of the parabola. Additionally, it is the parabola’s reflection line.
• Focus: A parabola’s focus is a fixed point that lies inside the curve and is connected to the vertex. The focus is above the vertex in an upward-opening parabola and below the vertex in a downward-opening parabola.
• Directrix: The vertex is connected to the directrix, which is a fixed line that is outside of the parabolic curve. Any point on a parabolic curve is defined to be equally distant from both the focus and the directrix.

There are many more advanced properties, but for the purpose of a go-over, these are sufficient.

Applications of Vertex of Parabola

There are numerous uses for a parabola’s vertex, including:

Parabolic curves are used to simulate the trajectory of projectiles and satellites in engineering and physics. The highest or lowest point in the trajectory is represented by the vertex of the parabolic curve.

The vertex of a parabolic curve can be used in finance to model how an investment will grow over time.

Parabolic mirrors are used in optics to reflect light in a particular direction. The mirror’s focal point is represented by the vertex of the parabolic curve.

Formulas for Finding Vertex of Parabola

Standard Form

A parabola has the equation f(x) = ax² + bx + c, where a, b, and c are constants. The formula (h, k) can be used to determine the vertex of a parabola, where h = -b/2a and k = f(-b/2a). The vertex’s x- and y-coordinates are represented by the letters h and k, respectively.

If a, b, and c are constants, the standard form equation of a parabola opening left/right can also be written as f(y) = ay² + by + c. The formula (h, k) can be used to determine the vertex of a parabola, where h = f(-b/2a) and k = -b/2a. The vertex’s x- and y-coordinates are represented by the letters h and k, respectively.

Vertex Form

A parabola opening upward/downward vertex form equation is f(x) = a(x – h)² + k, with a, h, and k being constants. The ordered pair (h, k), which corresponds to the vertex’s x and y coordinates, provides information about the parabola’s vertex.

A parabola opening left/right vertex form equation can also be written as f(y) = a(y – k)² + h, with a, h, and k being constants. The ordered pair (h, k), which corresponds to the vertex’s x and y coordinates, provides information about the parabola’s vertex.

Slope-intercept Form

The x-intercepts of the parabola opening upward/downward (p, 0) and (q, 0) are used in the intercept form of equation f(x) = a(x – p)(x – q). The equation h = (p + q) / 2 k = f(h), where h is the vertex’s x-coordinate, and k is its y-coordinate, is used to find the vertex at (h, k).

The y-intercepts of the parabola are (0, p) and (0, q), and the equation f(y) = a(y – p)(y – q) is written in the intercept form. The formula for locating the vertex (h, k) is k = (p + q) / 2 h = f(k), where h is the vertex’s x-coordinate, and k is its y-coordinate.

Solved Examples Involving the Vertex of a Parabola

Given the parabolic equation y = 2(x + 1)² – 5, find the vertex of the parabola.

Solution

First, we complete the square to put the equation in vertex form.

y = 2(x + 1)² – 5

y = 2(x² + 2x + 1) – 5

y = 2(x² + 2x + 1 – 1) – 5 + 4

y = 2(x + 1)² – 5 + 4

Then, we identify the x-coordinate of the vertex as the value of h:

h = -1

Next, we use the x-coordinate to find the y-coordinate of the vertex:

k = y(-1) = 2((-1) + 1)² – 5 + 4

y(-1) = 2(0)² – 5 + 4 = -1 + 4 = 3

So, the vertex of the parabola is (h, k) = (-1, 3).

All mathematical drawings and images were created with GeoGebra.

Velocity Definition < Glossary Index > Vertical Definition