Vertical|Definition & Meaning

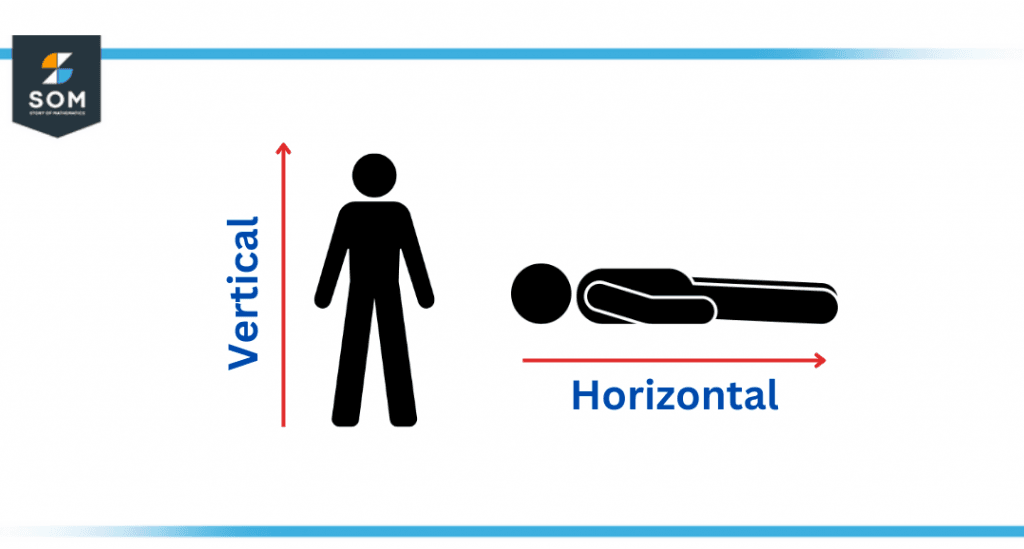
Figure 1 – Difference between Vertical and Horizontal

The term vertical is commonly used with vector quantities such as distance, altitudes or angles. The vertical distance can be expressed on the basis of where it is being measured or used. Such as vertical height, which is the distance between two points, where one point is claimed as a reference, and the other sits right above it at some space, and such a distance is measured upwards along a perpendicular line.

Similarly, vertical depth is the distance between two points, where one point is set as a reference and the other lies right below it with some gap. Such distance is measured downwards alongside a perpendicular line.

What Does Vertical Mean?

Vertical is a phrase used in geometric terms where a precise up or down location is being conveyed. Vertical may also be referred to as:

Vertical Direction

In the field of astronomy, topography, and other associated disciplines and environments, a direction or a level excelling by a specified reference point is known to be vertical if it is subjected in the direction of the force of gravity at that point. Conversely, the perpendicular distance to the vertical plane is known as horizontal.

• Historical Meaning
  The term vertical is a result of a late Latin word, “verticalis,” which has a close relationship with the roots of the vertex, which means the ‘highest possible point‘ or, more accurately, the “point where one starts to turn” as in a swirl.
• Geophysical Meaning
  • The plumb line
    In modern physics, household construction, and civil engineering, the path that is along the hanging plum-bob is usually designated as vertical.
  • The rotating body
    When we consider the rotatory behavior of our planet earth, the perceptions of vertical are compromised, giving it another meaning of its own. On the external plane of an evenly circular, consistent, non-revolving planet, the plumb bob directs as a vertical in a radial direction.

    Usually, the vertical walls sticking out toward the clear sky don’t tend to be parallel, as they all intersect at the median point. This theory is practically implemented in various construction projects as well as in civil engineering.

Figure 2 – Vertical Walls are not parallel on a sphere

• Mathematical Meaning
  • Two-dimensional perspective
    When we are in the perspective of an orthogonal Cartesian coordinate system, to declare a line to be a vertical one, the starting point or an initial label has to be prepared. Usually, the Y direction is labeled as the vertical, whereas the X direction is its counterpart, i.e., the horizontal level. In such cases, determining one direction can easily help in defining the other direction. These directions act as a pair in every respect.

    The vertical lines do not possess the power to cross each other or intersect at any point, as they tend to be parallel in nature. If there is a point P on the plane, then there can be only one vertical line within that plane. These facts somehow change in 3D geometry.

  • Three-dimensional perspective
    In three-dimensional geometry, the horizontal and vertical planes are an addition to the horizontal and vertical lines, thus making the situation a little more complicated. In 3D space, the symmetry that holds in the 2D doesn’t exist.

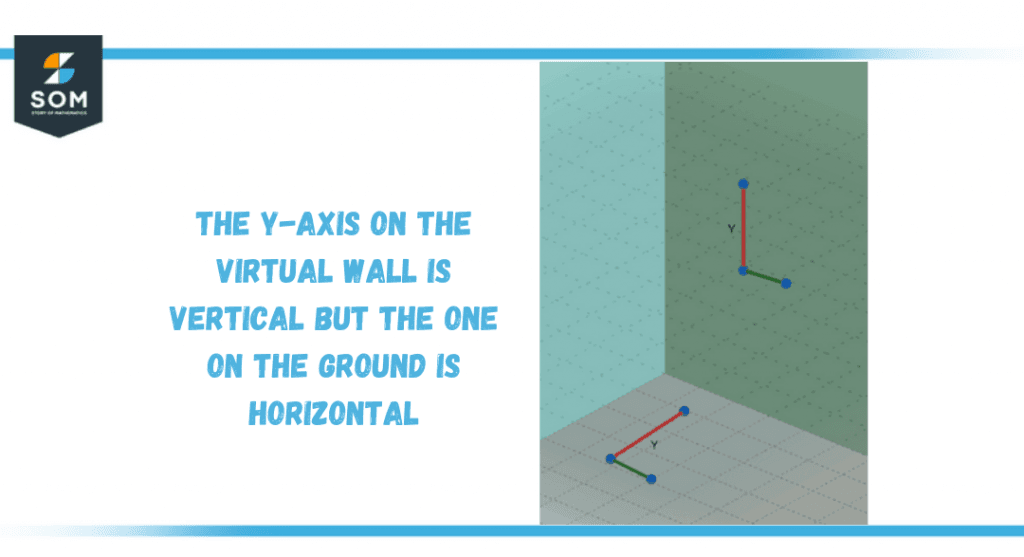
Figure 3 – Vertical lines are different in different perspectives

Vertical Angles

When a pair of vertical lines cross each other at some certain point, a total of four distinct angles are formed. These angles come in opposite pairs and are named relative to their location on each side.

Usually, when two straight lines intersect each other, they form an “X” shape, and thus the angles formed on the vertices of this shape are known as vertical angles or vertically opposite angles.

This equality in the opposite angles is known by the vertical angle theorem, and according to this theorem, the opposite pairs of vertical angles are equal in measure as both pairs are supplementary to the adjacent angles. A line is formed when two adjacent angles meet each other, thus called supplementary.

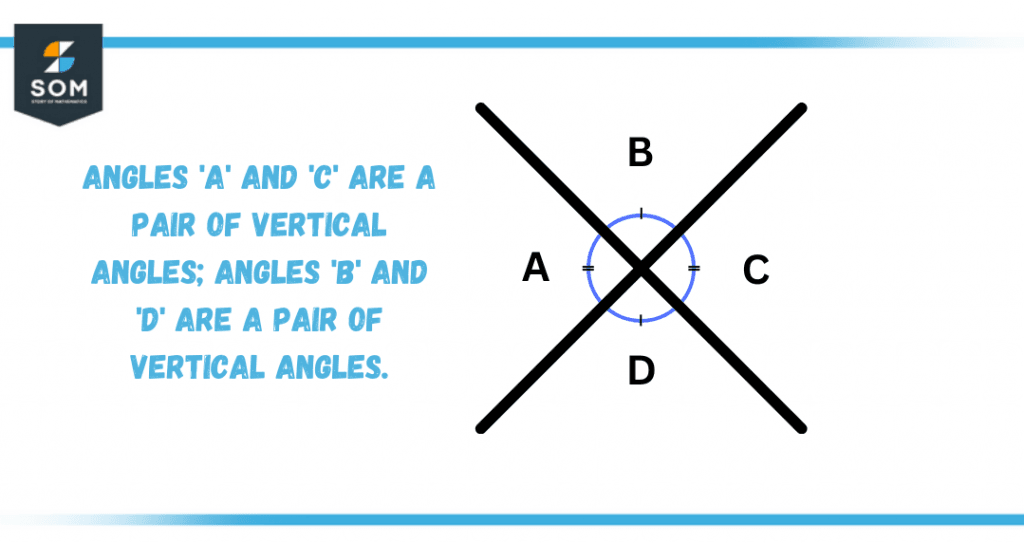
Figure 4 – Vertical Angles

Units of Vertical

Orthometric height is a vertical distance that can be stated in various units, including feet, meters, etc. Some vertical coordinates, such as geopotential numbers, are not based on typical length units.

Tools for Measuring Verticality

Altimeter

A device used to measure an object’s altitude above a given level is an altimeter or an altitude meter.

Bathymetry, the term used to describe the measurement of underwater depth, is connected to the term altimetry, which is used to measure altitude.

Bathymetry

The study of the underwater depth of the ocean, lake, or river bottoms is known as bathymetry. In other terms, bathymetry is the geography or hypsometry of the ocean.

Depth Gauge

An instrument used to measure depth below a surface of reference is a depth gauge. They consist of engineering tools for measuring the depth of holes and indentations from a reference surface as well as depth gauges for underwater diving and related applications.

Vertical Vs. Horizontal

The word vertical refers to the space measured from top to bottom, whereas horizontal refers to the measurement from right to left.

Vertical Scale Vs. Horizontal Scale

When we scale up the computing power of a device, we are merely referring to the vertical and horizontal scales of that device. The addition of more computer resources to your system is termed horizontal scale uplifting. But if you add more internal resources, such as a memory expansion or a faster processor, to that existing system, then it is referred to as the vertical scale.

In our daily usage, vertical scaling has become more common as it is better to buy a powerful computer than to rely on two of the same devices. But in an organization-based environment, the horizontal scale is far more common as more than one computer is working on the same query or service.

This phenomenon can be really handy in other practical environmental resources. Such as, transporting a bunch of people on a bus is vertical scale, whereas all of those people traveling in their individual cars is an example of a horizontal scale.

Vertical Integration Vs. Horizontal Integration

Not only are vertical and horizontal used in mathematical terms, but they have been proven to be quite handy in the business sector. The term horizontal integration is commonly used in businesses that are enhancing their growth by increasing their production by staying at the same supply chain level as their previous products.

Whereas when a business enters a new set of domains in its current level of the supply chain, it is known as vertical integration. For example, a jam company introduces peanut butter in horizontal integration, whereas the same jam company grows its own fruit for the jam in vertical integration.

Example of Verticality in Real Life Situations

Provide some real-life examples or scenarios where verticality is involved.

Solution

The walls in our homes, offices, or hotels are vertical unless there is a serious issue with them, or they are modeled in reference to the leaning tower of Pisa. A straight wall emerges at a perpendicular angle from the ground, straight up.

As opposed to when you are resting horizontally on a sofa, you are vertical when you are in an upright position.

Any object that has an upright posture will always have a vertical alignment, whereas an object lying down on its back will have a horizontal alignment.

Since the alphabet “v” faces down, it is easy to hark back to which direction is vertical.

All images/mathematical drawings were created with GeoGebra.

Vertex Parabola Definition < Glossary Index > Vertical Flip Definition