JUMP TO TOPIC
Vertical Flip|Definition & Meaning
Definition
A vertical flip is the same drawing of any item or figure but flipped vertically so that it appears upside-down. It is sometimes called a “water reflection.”
In the reflection, the highest point appears as the lowest point, while the lowest point appears as the highest.
Furthermore, this applies to anything ranging from an item to a linear graph.
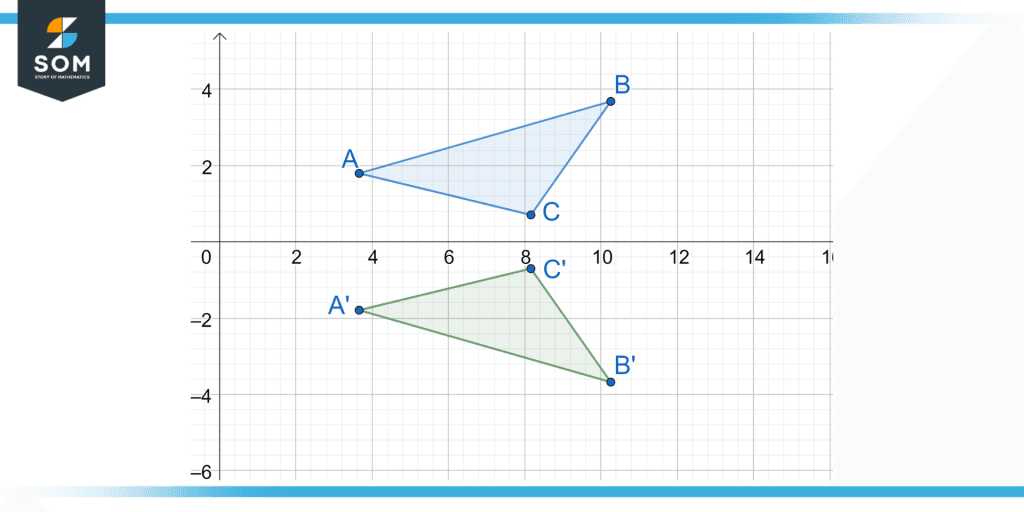
Figure 1: A triangle vertically flipped to be shown upside-down along the x-axis
Vertical reflection or vertical flipping is commonly used to simplify things by looking at them from a different perspective. Reflection has numerous uses in mathematics, real-life architecture, and graphs as well. Moreover, it’s fairly easy to redraw a reflection of a graph and this helps in finding solutions to problems quickly.
Vertical flipping is a type of reflection that reflects a figure or a graph with respect to the horizontal line. Its properties are very significant in its real-life applications, which further makes it much more viable in transformations and graphical conversions such as Laplace or Fourier transforms.
Properties of Vertical Flipping
A vertical flipping consists of a horizontal reference line, “Line of Reflection,” that is parallel to the x-axis and converts the image into an identical but vertically inverted image. Every point on the image is equidistant to the line and hence this is a very important property of a vertical reflection. Furthermore, if the line of reflection is not parallel to the x-axis, we will not achieve a properly vertically flipped image on the other side of the line.
Moreover, the reflected version of the image will look upside-down as compared to the original figure due to each point of the image being at an equal distance from the line of reflection as the same point on the original image. This property helps in photography such as taking pictures of a lake and a mountain that has a vertical reflection made on the lake.
In general, these reflections also act in creating new and easier images using the symmetry concept, where one part of the figure is identical but mirrored to the other part of the figure which makes it a complete figure when coupled together. These figures have a line of reflection in the midpoint of the figures where each side is identical to the other. The line of reflection can be either vertical or horizontal given that the sides of the figure are identical in that case.
Comparisons With Horizontal Flipping
The concept of reflections is the same for horizontal flipping as for vertical flipping. The only difference that is observed in the two types of flipping is the line of reflection. Vertical flipping has a line of reflection that is parallel to the x-axis, whereas the line of reflection is parallel to the y-axis for horizontal flipping.
Horizontal flipping is usually seen in our daily lives in mirrors. The figure that we see of ourselves in a mirror is inverted horizontally and hence, this is the reason our left-hand looks like a right and our right-hand looks as if it is left in the mirror. The line of reflection of the mirror is the plane parallel to the mirror and it is the reason why the figure that we see is inverted.
Figure 2: Horizontal flipping of a graph with the line of reflection parallel to the y-axis
Moreover, horizontal reflection is also used to transform graphs and to help find their solution by looking at them from a different perspective. This application is similar to what vertical flipping helps in doing.
Additionally, besides horizontal flipping, other transformations such as rotation, transformation, and dilation play a similar role in helping find the implicit meanings and solutions to different figures or graphs.
Construction of a Graph Undergoing a Vertical Flip
To construct a vertical reflection of a graph alongside an x-axis as the line of reflection, all you need is to multiply the y-coordinates of the graph by -1. The condition here is that you have graph paper available and the line of reflection is the x-axis. In case we have a line of reflection parallel to the x-axis, we would require to follow the steps below:
- First, measure and draw a line from each point of the graph perpendicularly to the line of reflection.
- After that, draw a perpendicular line of the same length on the other side of the line of reflection
- Finally, join all the points that have been drawn on the graph on the opposite side of the line of reflection.
By this process, we would be able to achieve a vertically flipped version of the graph or a figure on the other side of the line of reflection.
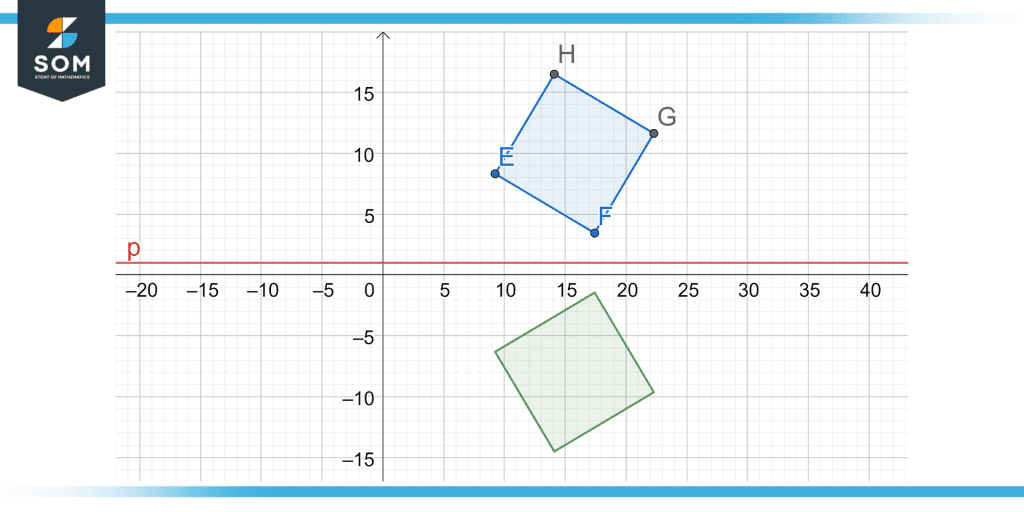
Figure 3: A parallelogram being reflected vertically and its points being reflected on a line of reflection y = 1
An Example Depicting the Usage of a Vertical Flip
We are given a linear graph “y = 2x +1” in the positive half of the x-axis. Find and draw the vertical reflection of the graph, where the line of reflection is the x-axis
Solution
To find the reflection of the graph y = 2x + 1, all we require is to invert the y-coordinates of the graph to acquire the reflection of the graph at the line of reflection being the x-axis.
This graph is a linear equation that can be generalized by the formula, y = mx + c. The y-intercept “c,” is equal to +1 in this curve. For the reflected graph, the y-intercept c` will be equal to c` = -1 * c = -1(1) = -1. Hence, the c is equal to -1.
Furthermore, since it is a reflection, the graph must have a negative proportionality as compared to the original line, which will cause the x-axis to be equidistant from both graphs. Hence, the gradient “m” must be multiplied by -1 as well. This value will be equal to:
m’ = 2x * (-1)
m’ = -2x
Thus, the resulting reflected line will have the formula “y = -2x – 1.”
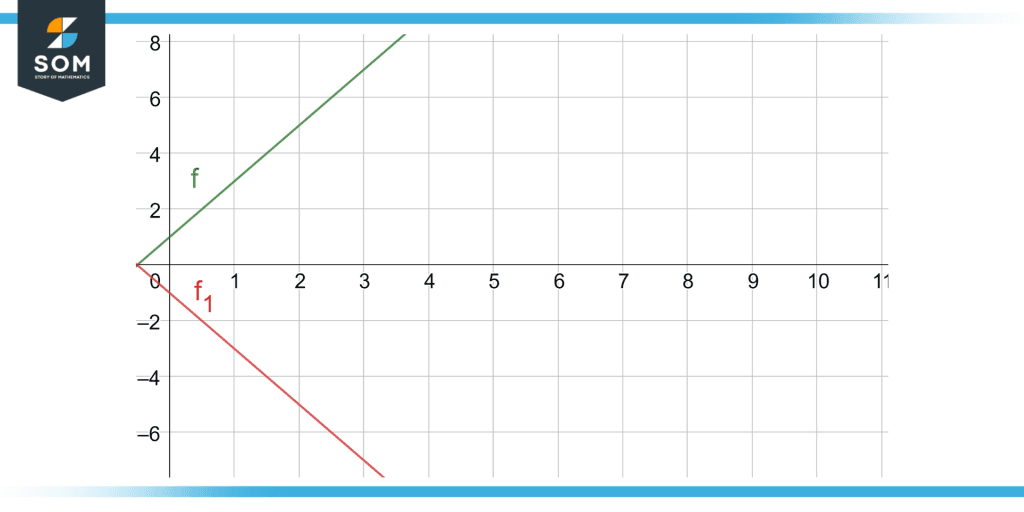
Figure 4: A graph showing the reflection of the line y = 2x + 1 reflected on the x-axis.
All the graphs and figures were created using GeoGebra.
