JUMP TO TOPIC
Vertices|Definition & Meaning
Definition
Vertices are the plural of vertex, which is any one of the corner points of a shape. Therefore, a vertex is a point where two or more line segments join together, so it follows that different shapes have different numbers of vertices (e.g., a triangle has 3 vertices while a square has 4, a pyramid has 5 while a cube has 8, etc.). They are one of the defining features of shapes.
Figure 1 shows the vertices of a triangle and a square.
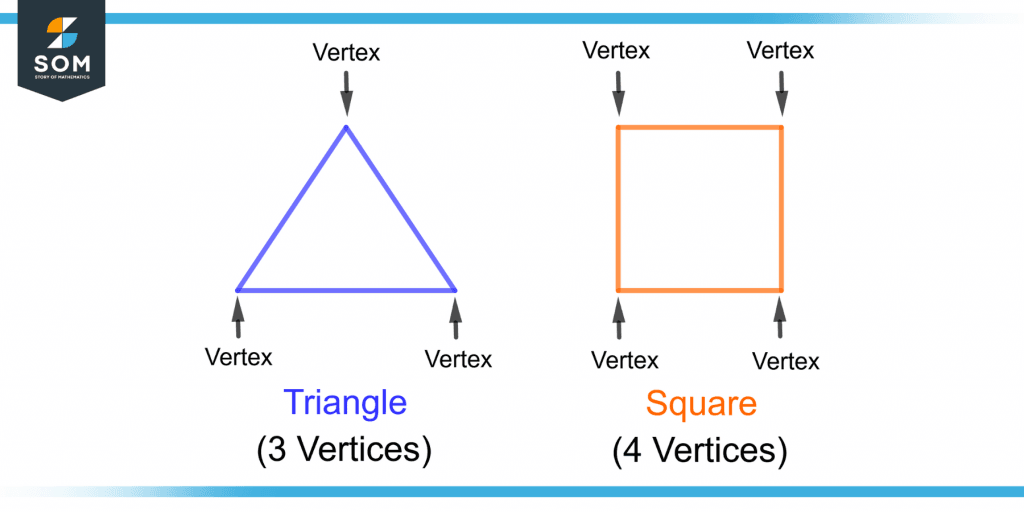
Figure 1 – Demonstration of Vertices of a Triangle and a Square
Polygon
A polygon is a two-dimensional shape bounded by straight lines. It is a plane or flat shape, not having curved surfaces. A polygon consists of sides, also known as edges. The points or corners where two edges meet are called the vertices.
Different types of polygons include a triangle, quadrilateral(square, rectangle, parallelogram), pentagon, hexagon, heptagon, octagon, nonagon, and decagon.
Polyhedron
A polyhedron is a three-dimensional solid with straight edges, sharp vertices, and flat polygonal faces. Spheres and cones are not considered polyhedrons as they do not have polygonal faces. Cubes and pyramids are examples of polyhedrons.
Other Defining Features of Polygons and Polyhedrons
The number of vertices in a polygon or a polyhedron defines its structure. Other important features that define their shape’s symmetry are their edges, faces, and sides. These are discussed as follows.
Faces
The term “faces” is only used for polyhedrons. The outer flat surfaces of a polyhedron are its faces. A cube has six faces, and a pyramid has five faces. An individual face of a polyhedron forms its respective polygon.
Figure 2 shows the faces of a rectangular prism that has eight vertices.
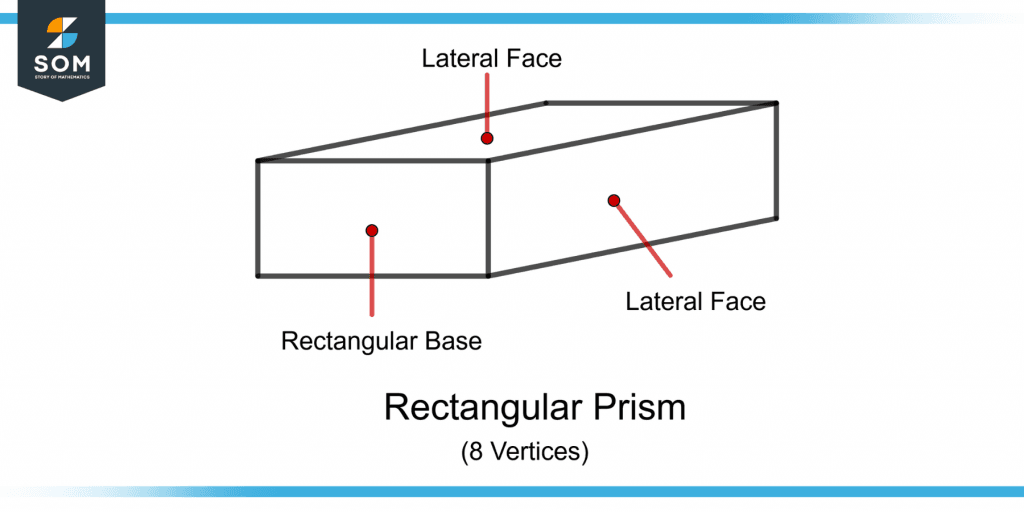
Figure 2 – Demonstration of Six Faces of a Rectangular Prism with Eight Vertices
A rectangular prism has six faces with four lateral faces and two faces known as rectangular bases. A base shape of a prism defines the type of prism.
Edges
An edge of a polygon is the line segment joining any two adjacent vertices. For example, a hexagon consists of six edges. The edges of a polyhedron are simply the line segments around which any number of faces (at least two) meet.
Figure 3 shows the five edges of a pentagon(polygon) and some of the edges of a tetrahedron(polyhedron). A tetrahedron has a total of eight edges.
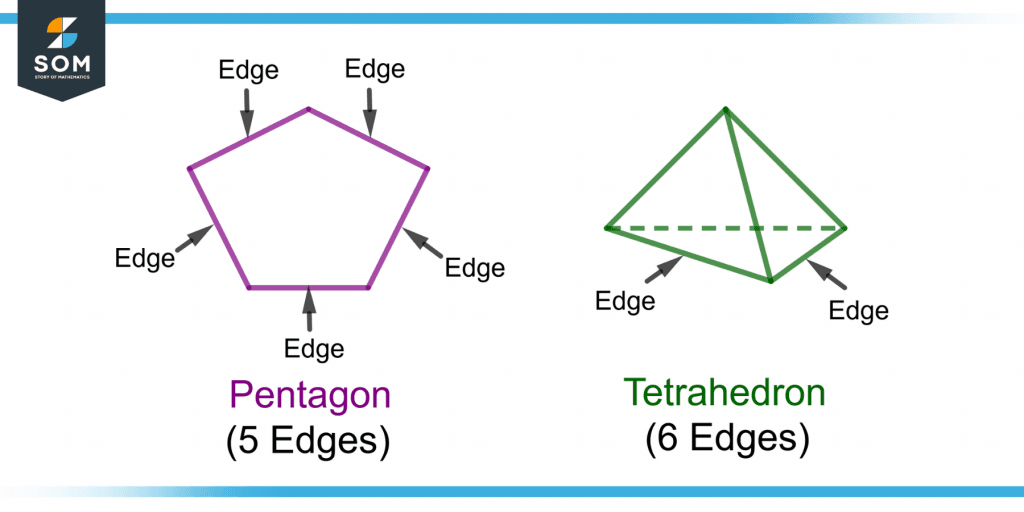
Figure 3 – Demonstration of Edges of a Pentagon(polygon) and a Tetrahedron(polyhedron)
Sides
The term “side” means different for a polygon and a polyhedron. The edge of a polygon can be referred to as the side of a polygon. A polyhedron’s face is also called one of its sides.
Adjacent Vertices
Adjacent vertices are the vertices next to each other. Two vertices are adjacent if they are joined by a side or an edge in a polygon. A hexagon is shown in figure 4.
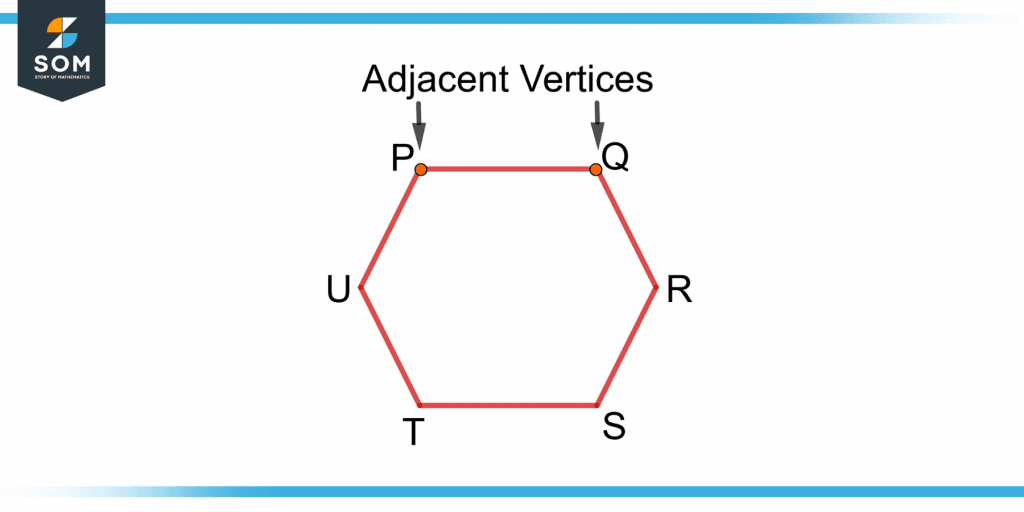
Figure 4 – Demonstration of Two Adjacent Vertices of a Hexagon
The vertices P and Q, R and S, and T and U are adjacent to each other as they are connected by an edge. The vertices P and R are non-adjacent, as there is no common edge between them.
Opposite Vertices
Opposite vertices are defined as the two vertices opposite to each other.
If two opposite vertices of a polygon are joined by a line segment, then that line segment is known as the diagonal. A triangle has no diagonal, as there are no opposite vertices in a triangle.
Figure 5 shows a rectangle LMNO.
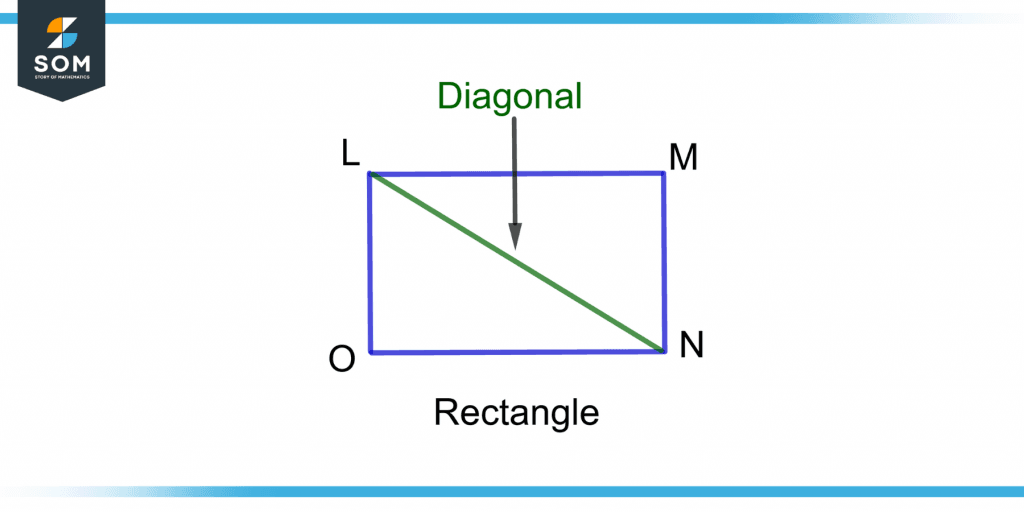
Figure 5 – Demonstration of Opposite Vertices and a Diagonal drawn with Two Opposite Vertices
The two vertices, L and N, and M and O of the rectangle are opposite to each other. A diagonal can be formed by joining any of these two opposite vertices.
Diagonal Formula
We can evaluate the number of diagonals of a polygon by using the formula given as:
Number of Diagonals = [m(m-3)] / 2
Where “m” is the number of vertices of an m-sided polygon.
For example, to calculate the number of diagonals of a nonagon, the number of vertices or the sides of the nonagon should be known. A nonagon has nine sides and nine vertices, so:
m = 9
Putting the value of m in the above formula gives the total number of diagonals of a nonagon as:
Number of Diagonals of a Nonagon = [9(9-3)] / 2
Number of Diagonals = 9(6) / 2 = 54 / 2
Number of Diagonals = 27
Hence, a nonagon has a total of 27 diagonals.
Euler’s Formula
Euler’s formula gives a relation between the edges, vertices, and faces of a polyhedron. It states that the sum of the number of vertices and the number of faces of a polyhedron is equal to the number of edges plus two. It is given as follows:
V + F = 2 + E
Where V, F, and E are, respectively: the number of vertices, the number of faces, and the number of edges. This formula can also be written as:
V + F – E = 2
Hence, the number of edges subtracted from the sum of the number of vertices and faces of a polyhedron always equals two.
For example, a triangular prism has 4 faces, 4 vertices, and 6 edges. Putting the values in Euler’s formula gives:
4 + 4 = 2 + 6
8 = 8
A triangular prism is also known as a tetrahedron.
Euler’s formula works for almost all polyhedrons except the solids with holes in them.
Platonic Solids
A platonic solid is a solid having all the faces as the same regular polygons. A regular polygon has all the sides of equal length and all its angles congruent to each other. Also, an equal number of polygons are joined at each vertex of a platonic solid.
The five major platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
A tetrahedron has four vertices, with each vertex joining three triangles. It has four faces and six edges. A cube has eight vertices joining three squares at each vertex. It has six faces and twelve edges.
An octahedron has six vertices with four triangles joined at each vertex. It has eight faces and twelve edges. An icosahedron has five triangles meeting at each of its twelve vertices. It consists of twenty faces and thirty edges.
Vertex of an Angle
An angle is formed by joining two rays at a common point. This common point is also known as the vertex of the angle. Figure 6 shows the demonstration of the vertex of an acute angle.
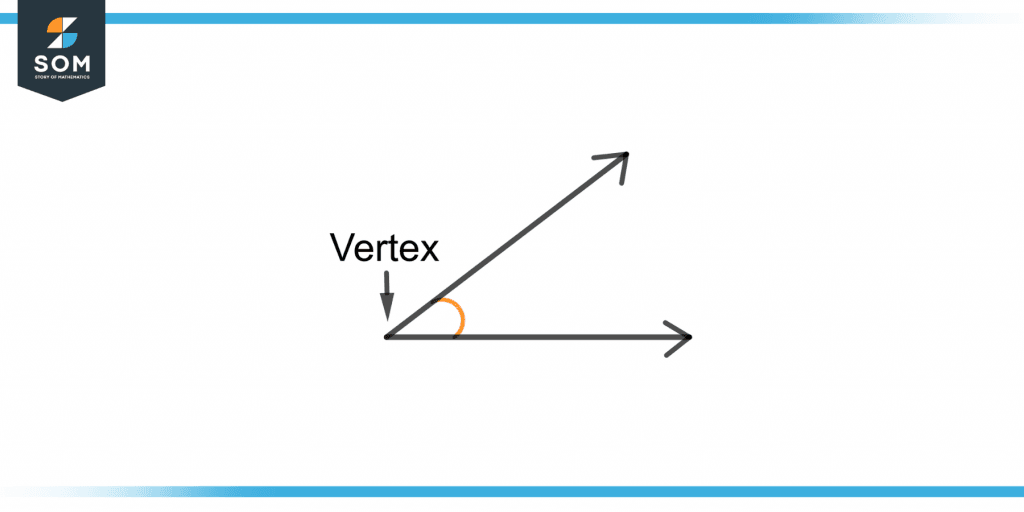
Figure 6 – Illustration of a Vertex of an Acute Angle
Examples of Vertices
Example 1 – Identifying Vertices
Identify the number of vertices of a heptagon. Calculate the number of diagonals that can be formed by the opposite vertices of a heptagon and draw these diagonals. Also, identify any two pairs of adjacent vertices and opposite vertices of the heptagon.
Solution
A heptagon has seven edges or sides. It has a total of seven vertices. The number of diagonals of a heptagon can be calculated by using the formula:
Number of Diagonals = [m(m-3)] / 2
Here, m = 7, putting the value of m gives:
Number of Diagonals = [7(7-3)] / 2
Number of Diagonals = [7(4)] / 2 = 28 / 2
Number of Diagonals = 14
Hence, a heptagon has a total of 14 diagonals shown in figure 7.
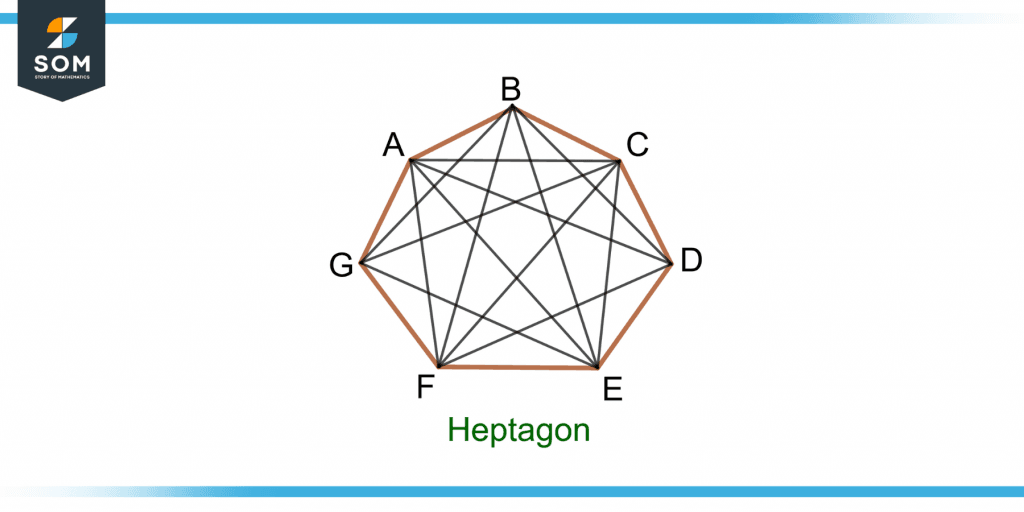
Figure 7 – Illustration of Total Number of Diagonals of a Heptagon and its Vertices
The vertices A and B are adjacent vertices, and the vertices A and D are two opposite vertices of the heptagon.
Example 2 – Using Euler’s Formula To Calculate the Number of Vertices of a Platonic Polyhedron
Calculate the number of vertices of a dodecahedron having twelve faces and thirty edges.
Solution
Euler’s formula is given as follows:
V + F – E = 2
For a dodecahedron:
F = 12 , E = 30
For the number of vertices V, the formula becomes:
V = 2 – F + E
Putting the values of F and E gives:
V = 2 – 12 + 30
V = 2 + 18
V = 20
Hence, a dodecahedron has twenty vertices.
All the images are created using GeoGebra.
