Vinculum|Definition & Meaning

A grouping sign in mathematics is called an overbar symbol (as well known as a vinculum). To indicate that a set of numbers or letters is present, a horizontal line is placed over them. A vinculum is another name for the fraction bar, which is the bar that separates a fraction’s numerator and denominator.

In mathematics, the bar over a letter could stand for any of the following: compliment, line, or vinculum.

Illustration

In the year 1646, Frans van Schooten was the first person to introduce vinculum to the world. Also, some initial attempts were made by scientists such as Chuquet during the period 1484 and Descartes in the period 1637. These are examples of early attempts.

Particularly when the earlier notational norms are first introduced in school, recurring decimals are sometimes symbolically expressed by an ellipse (three periods, 0.333…). A straight horizontal line placed across or between numbers two or more members of a complex mathematical statement; this mark is comparable to surrounding those members with parentheses or brackets.

A horizontal line known as a virnaculum can be found in mathematical notation. The Latin term virnaculum, which can also be written as viniculumn, can signify either chain or knot. In any mathematical problem, the linear perspective above or below signifies that the two conditions should be evaluated together or in a group.

This is the most fundamental significance of the horizon line.

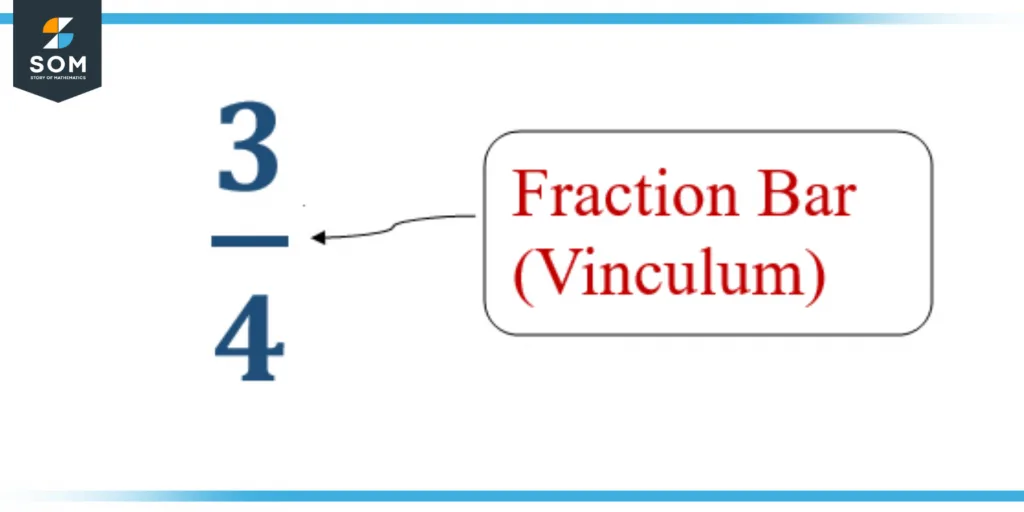
Figure 1 – Vinculum Representation

Here in this figure, The horizontal line between the two numbers 3 and 4 is vinculum.

A vinculum or virnaculum is a phrase that is used to describe a group of concepts or the fact that they are together. It is a Latin term that literally translates to “tie,” and as a result, the meaning of the symbol is “linked together.”

In the past, vinculum was extensively employed to denote that the provided terms are together, but these days, this role is typically performed by parentheses or round brackets instead.

The purpose of the vinculum at this point is to denote the recurrence of something. The number 5, for instance, appears as a repeated or recurring decimal in the equation that is provided below.

8 – (6 ÷ 4 + 3.555555) or we may say 8 – (6 ÷ 4 + 3.5)

Iterating the Decimal System

Terminating decimals make up the majority of all used digits in decimal form. A decimal that carries on endlessly and repeats a numerical or block of numerals in a consistent fashion is called a repeating decimal. Some examples of repeating decimals include 0.555… or 0.37777 or 0.232323… The usual notation for indicating that a numerical or group of digits is recurring is called a vinculum, which is a horizontal line placed over the numbers or data points in question. When represented by the vinculum, the repeated fraction appears as shown in the below figure.

Figure 2 – Vinculum in Decimals

Fraction Bars

A fraction bar is a graphical presentation of a fraction that can be used for comparison and operations using fractions in mathematics. An effective visual representation of the relationship between parts and the total is the use of fraction lines or fraction strips.

A fraction bar’s individual segment stands in for a single unit of measurement. It’s a representation of a subset of the whole, and for this reason, it’s called a “part-to-whole” representation.

Standard diagrams use a bar segmented into equal units, with the number of colored segments providing information on the number of components shown. Here’s a model with fraction bars to consider. The shaded region of the first column in the fraction columns below stands for two-thirds of the whole. Eight of the twelve components are shown by the second bar’s shading.

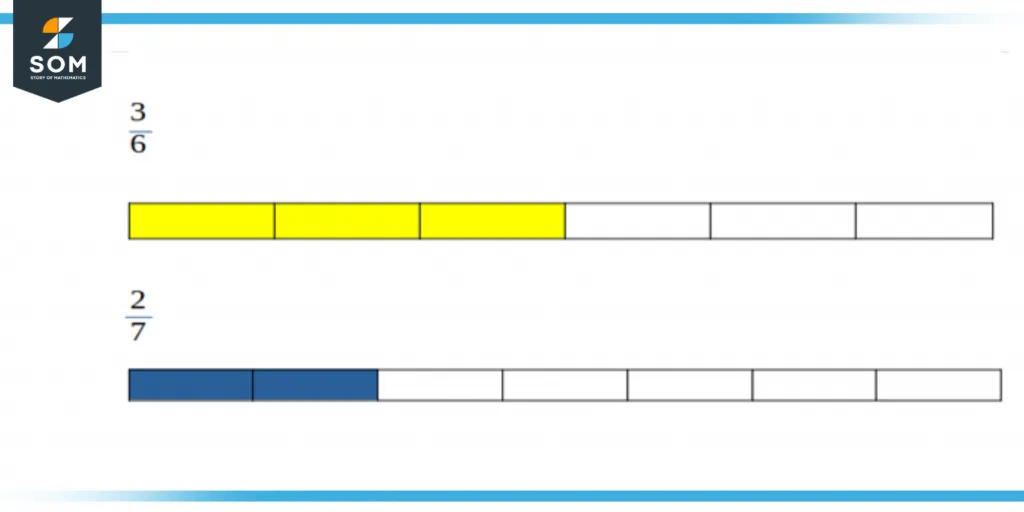
Figure 3 – Vinculum in Fraction

Practical Approach

In recent times, vinculum has been put to use in three primary applications. These applications are as follows:

1. As a kind of Boolean logic, it is utilized in the Boolean operators to represent the NOT operation or the inversion of the operation. As an illustration, Y = AB.
2. In geometry, the symbol of a bar or vinculum is used to depict a line segment. This symbol is also known as the vinculum. Take, for instance, the notation -AB, where A and B are indeed the beginning and ending endpoints of the vertical line.
3. Indicating a recurrent or repeating decimal with a bar or vinculum. The line or vinculum is the symbol that is used to signify a repeating or recurring decimal.

Consider the following: if one-third of one is 0.3333333

Further Explanation

As a method for grouping related information, it fills the same role as the parentheses: to denote a group within the context of a specific equation. For example, in the expression a * b – c, the bar that appears on b minus c shows that the two numbers are combined and that first the difference between them will be computed, followed by the multiplication by a.

It is a component of radical- and, when combined with both the radical sign and the vinculum, it produces the beneath root symbol, which is utilized frequently in modern times.

The line chart or bar used during mathematics is called a Virnaculum or Vinculum. Originally from the Latin vinculum, which meant “chain” or “knot,” this operation has a rich mathematical history. The bar or horizontal line serves a similar purpose by indicating that the terms on either side of it belong to the same set. The current beneath the root sign has its origins in its use as brackets or as a component of a radical.

In contemporary mathematics, virnaculum is used to denote a line segment, the inverted or NOT of any function with Boolean operators, and the repetition of a decimal with a bar above the repeating term.

Example of Vinculum Usage

Solve 1/7 as repeating decimals.

Solution

While solving this fraction, it gave us repeated answers like:

1/7 = 0.142857 =  0.1428571428571428571…

= $\mathsf{0.\overline{142857}}$

All the figures above are created on GeoGebra.

Vertices Definition < Glossary Index > Weight Definition