X Coordinate|Definition & Meaning

The x-coordinate 4 in (4, 3) is the signed distance from the origin to the point along the x-axis, as shown in figure 1.

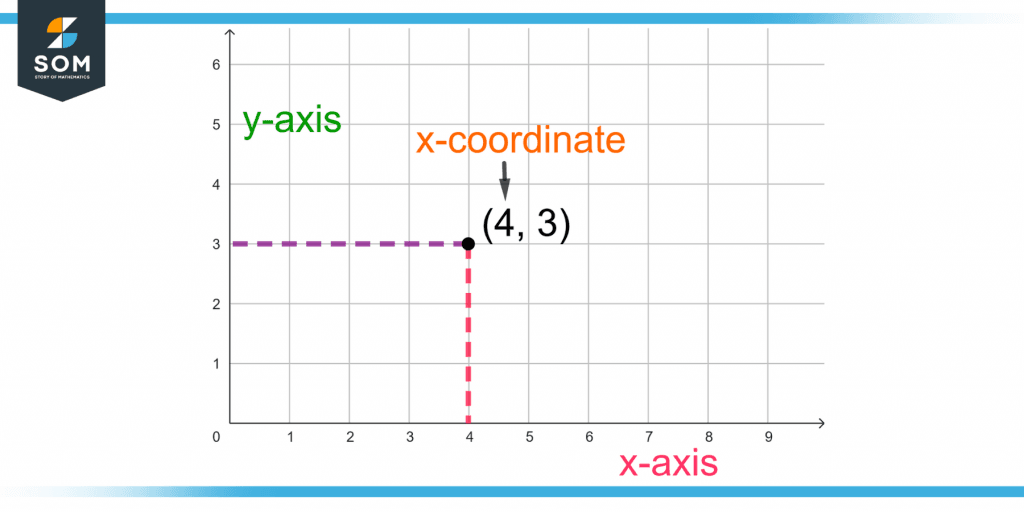
Figure 1 – Demonstration of the x-coordinate of a Point in an x-y-plane

Rectangular Coordinates

The rectangular coordinates, also known as the Cartesian coordinates, are the x and y coordinates on a graph in a two-dimensional plane. They are the signed distances from the origin to the point in the horizontal and vertical directions.

The signs with the x and y coordinate specify the direction of the distance from the origin. If a point’s coordinates are (a, b), then their distance from the origin is the absolute value of a and b.

Both the x and y coordinates form the Cartesian or orthogonal coordinate system. Without the y-coordinate, the x-coordinate alone cannot trace a point in a 2D plane. 

These numerical coordinates specify the position of a point by using two coordinate axes, the x and y-axis. For point A in a 2D plane, two lines, which are perpendicular to both axes, passing through point A, meet each axis at a number. These two numbers are the rectangular coordinates of point A.

The x and y coordinates are called rectangular coordinates, as locating the point through the coordinates forms a rectangle in the x-y plane. For example, point (7, 4) is located in the x-y plane, as shown in figure 2.

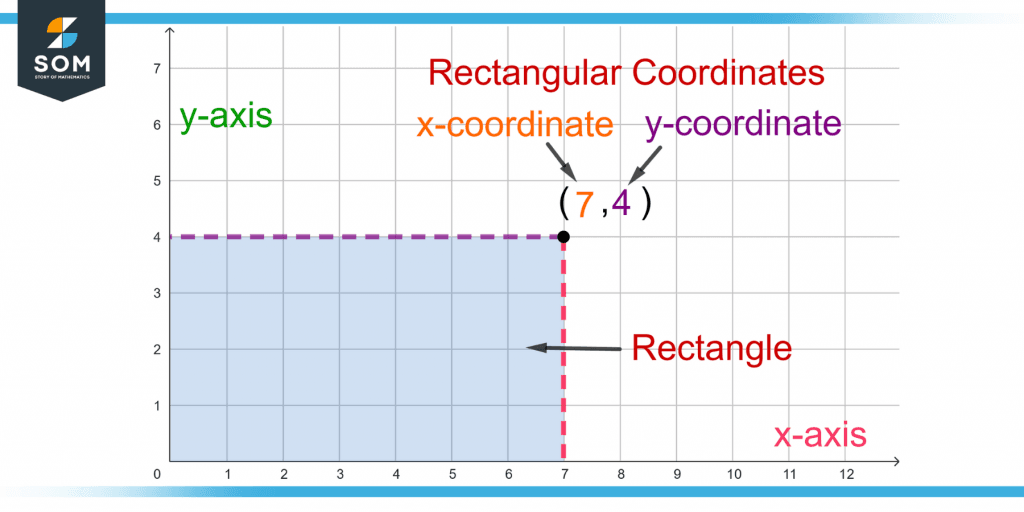
Figure 2 – Demonstration of a Rectangle Formed by Tracing a Point by Using Rectangular Coordinates

Ordered Pair

The rectangular coordinates are written in parentheses, separated by a comma as (x, y); the first coordinate is always the x-coordinate, and the second, is the y-coordinate. This notation (x, y) is known as an ordered pair. The x-coordinate is known as the abscissa, and the y-coordinate as ordinate.

For example, (2, 3) is an ordered pair showing the horizontal distance as 2(x-coordinate) units and the vertical distance as 3(y-coordinate) units from the origin.

Each point in the Cartesian coordinate system is specified by a unique ordered pair.

X-Axis and Y-axis

An axis is a reference line used to measure the distance from a certain reference point. The two axes in a two-dimensional plane are the x and y-axis. The two axes are placed in such a way that they are perpendicular to each other.

The horizontal axis is known as the x-axis, while the vertical axis is the y-axis. The left-right direction is the horizontal direction, and the up-down direction is the vertical direction.

Origin

The x and y axes can be considered as two number lines placed at right angles. The point at which both axes intersect is known as the origin. It is denoted by O with the ordered pair as (0, 0). It is the reference point from where any point can be traced by moving some units left, right, up, or down.

Directions of Positive and Negative X and Y Axes 

The direction of the positive and negative x and y axes are discussed below.

Positive X-axis

The positive x-axis moves from the origin O from left to right. The x-coordinate increases as we move further from left to right.

For example, point (5, 3) has the x-coordinate as positive five. It means that from the origin, going five units from left to right tells how much the point is along the positive x-axis. But to completely trace the point in a 2D plane, the y-coordinate 3 should also be considered.

Negative X-axis

The negative x-axis has a direction opposite to the positive x-axis. From origin O, the negative x-axis increases as we move from right to left. For example, point (-3, 4) has the x-coordinate as negative three. It means that from the origin, going three units from right to left shows the point along the negative x-axis.

Positive Y-axis

The positive y-axis increases in the upper direction from the origin O. This means that the y-coordinate increases as going more and more in the upper direction. For example, point (1, 6) has a positive six as a y-coordinate. It means that going six units up from the origin shows how much the point is far up on the positive y-axis.

Negative Y-axis

The direction of the negative y-axis is the opposite of the positive y-axis. The negative y-axis increases from the origin point in the downward direction. For example, point (2, -4) has a negative four as the y-coordinate. By moving four units down from the origin, the y-coordinate -4 is located.

Figure 3 shows the origin and the positive and negative x and y-axis.

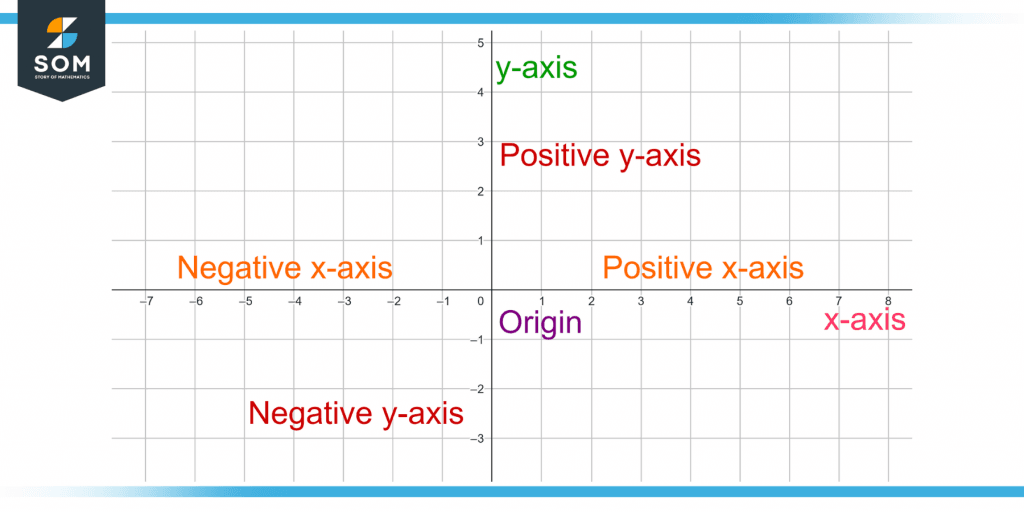
Figure 3 – Demonstration of Origin and Positive and Negative x and y-axis

Four Quadrants

“Quad” means four. The x and y axes divide the Cartesian plane into four parts, known as the quadrants. The four quadrants are numbered in ascending order in a counter-clockwise direction. The four quadrants are discussed below.

First Quadrant

In the first quadrant, both the x and y coordinates are positive. This is the top-right quadrant which includes the positive x and y-axis. For example, the ordered pair (1, 3) belongs in the first quadrant as both the x-coordinate 1 and the y-coordinate 3 are positive.

Second Quadrant

In the second quadrant, the x-coordinate is negative, and the y-coordinate is positive. This is the top-left part of the Cartesian plane, including the negative x-axis and the positive y-axis. For example, point (-1, 3) lies in the second quadrant, moving left one unit and moving up three units from the origin.

Third Quadrant

In the third quadrant, both the x and y coordinates are negative. This is the bottom-left quadrant in the x-y plane with both the x and y axis negative. For example, the ordered pair (-1, -3) belongs in the third quadrant, moving one unit left and three units down from the origin.

Fourth Quadrant

In the fourth quadrant, the x-coordinate is positive, and the y-coordinate is negative. This is the bottom-right quadrant with a positive x-axis and a negative y-axis. For example, point (1, -3) belongs in the fourth quadrant, moving one unit right and three units down from the origin O.

Figure 4 shows the points (1, 3), (-1, 3), (-1, -3), and (1, -3) in the first, second, third, and fourth quadrants, respectively.

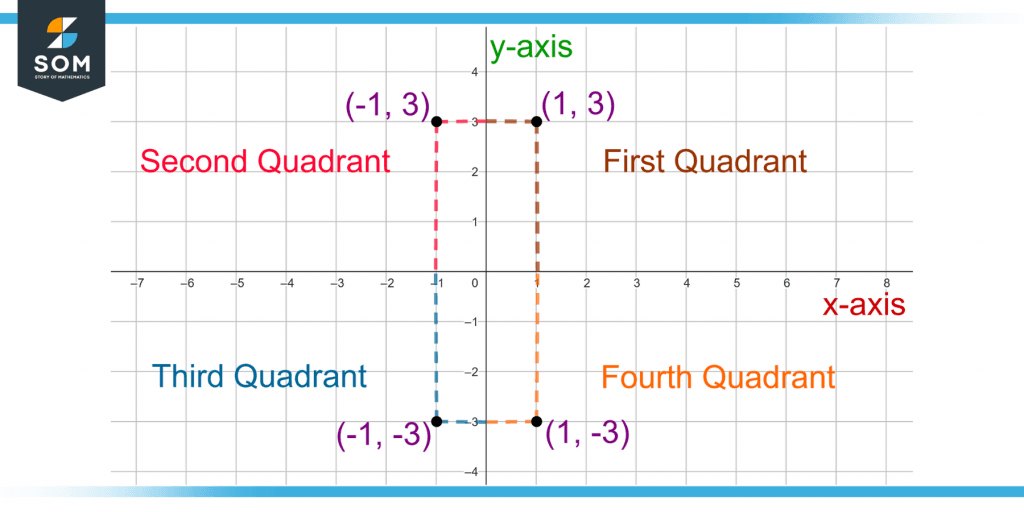
Figure 4 – Demonstration of the Four Quadrants and Locating a Point in all the Four Quadrants

X-coordinate in Different Dimensions

Different dimensions require a different number of coordinates to define a point or object in space. The x-coordinate in a different number of dimensions is discussed below.

One Dimension

One axis can be considered as a number line. A line is a one-dimensional figure, so it requires only one number to specify a point on a number line. The number line contains two half-lines, one positive half-line from to positive infinity and one negative half-line from zero to negative infinity.

Two Dimensions

Two dimensions consist of two axes, the x and y-axis. The x and y-coordinate specify a point in a 2D plane. Two numbers are required to identify a point in a 2D plane which determines the horizontal and vertical distance from the origin O.

Three Dimensions

A three-dimensional space consists of an x, y, and z coordinate. Three lines drawn at right angles to each other are the x, y, and z axis in space. The point where the three axes intersect is the origin O.

The x-coordinate shows how much to move left or right from the origin. The y-coordinate shows how much to move up and down from the origin, and the z-coordinate shows how much to move backward or forward to get from the origin to the point in space.

Distance Between Two Points in an X-Y Plane

The distance between two points in an x-y plane can be found by using the x and y-coordinates of the points. If the coordinates of point C are (x₁, y₁) and those of point D are (x₂, y₂), the distance between point C and D can be calculated by using the formula:

\[ \text{Distance} = \sqrt{ {( y_2 \ – \ y_1 )}^2 + {( x_2 \ – \ x_1 )}^2 } \]

Examples Involving the X Coordinate

Example 1 – Identifying X and Y Coordinates of an Ordered Pair

Point Q is shown in an x-y plane in figure 5. Identify the x and y coordinates and write the ordered pair of the point Q.

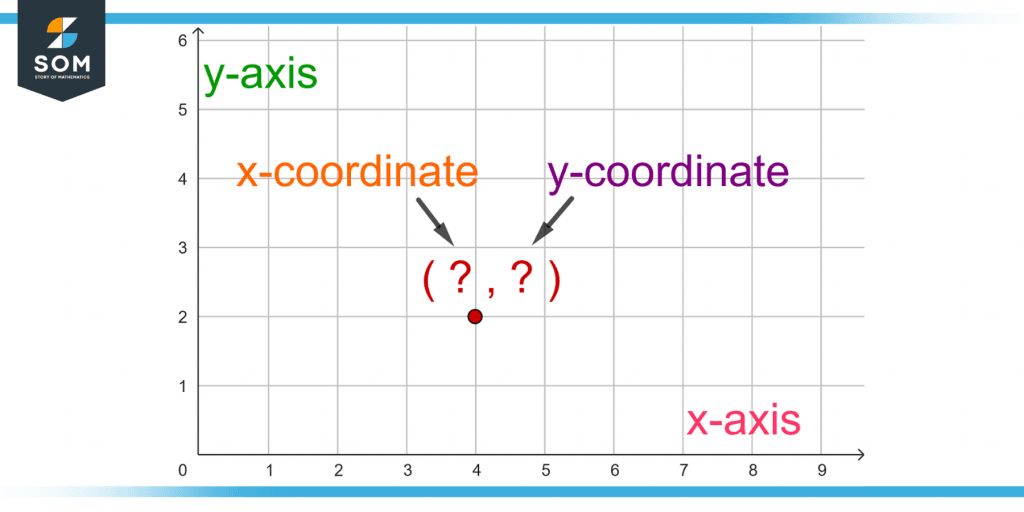
Figure 5 – Identifying the x and y-coordinates of a Point in a x-y Plane

Solution

At first, two lines that pass through point Q and are perpendicular to the two axes are drawn such that they meet the x and y axis at the x and y coordinates of point Q, respectively. Hence, the x-coordinate is 4, and the y-coordinate is 2. It can be written as an ordered pair as (4, 2).

Example 2 – Identifying the Quadrants of Different Ordered Pairs

In which quadrants do the ordered pairs (-9, -3), (-1.4, 12), (3, 7), and (8, -5) lie?

Solution

The point (-9, -3) lies in the third quadrant as both the x and y-coordinates are negative.

The point (-1.4, 12) lies in the second quadrant as the abscissa is negative, but the ordinate is positive.

Point (3, 7) lies in the first quadrant as both the x and y coordinates are positive.

The ordered pair (8, -5) lies in the fourth quadrant as the abscissa is positive, but the ordinate is negative.

Example 3 – Finding the Distance Between Two Points

Find the distance between two points, T with coordinates (2, 6) and R with coordinates (5, -8).

Solution

The formula for the distance between two points is given:

\[ \text{Distance} = \sqrt{ {( y_2 \ – \ y_1 )}^2 + {( x_2 \ – \ x_1 )}^2 } \]

Taking the coordinates of T as (x₁, y₁) and the coordinates of R as (x₂, y₂).

So:

x₁ = 2, y₁ = 6, x₂ = 5, y₂ = -8

Putting the values in the distance formula gives:

\[ \text{Distance} = \sqrt{ {( – 8 \ – \ 6 )}^2 + {( 5 \ – \ 2 )}^2 } \]

\[ \text{Distance} = \sqrt{ {( -14 )}^2 + {( 3 )}^2 } \]

\[ \text{Distance} = \sqrt{ 196 + 9 } \]

\[ \text{Distance} = \sqrt{ 205 } \]

Distance = 14.3

All the images are created using GeoGebra.

X Axis Definition < Glossary Index > Y Axis Definition