JUMP TO TOPIC
Hypergeometric Calculator + Online Solver With Free Steps
The Hypergeometric Calculator is a useful tool for quickly determining the probability of success in an event without any replacement in its occurrence. The calculator takes some values regarding the event as input.
The Calculator displays the probability of success of the event under observation in different forms like fractions, decimals, number lines, etc.

What Is a Hypergeometric Calculator?
Hypergeometric Calculator is an online calculator that is specifically designed to find the success probability of an event without replacement. This calculator is specifically designed for events that cannot reoccur.
This calculator is a beneficial tool for quickly solving complex hypergeometric problems in a few seconds. It is free of cost and can be accessed unlimited times with any good browser.
How To Use the Hypergeometric Calculator?
You can use the Hypergeometric calculator by entering the required values regarding the specific event in spaces given for the respective values. The calculator needs population, success in population, sample size, and successes in the sample
For each value of input data, there is a labeled box. You should follow the steps mentioned below to use the calculator properly.
Step 1
Enter the population size in the box labeled Population Size and in the second box enter the number of successes.
Step 2
In the box labeled Sample Size, enter the size of the sample taken from the population. Similarly in the last box, labeled as Successes in Sample enter the number of successes in the sample.
Step 3
Now, click on the Submit button to start the calculation of the results.
Result
The result is displayed in different sections. The first section displays the input values put in the formula of the hypergeometric distribution.
The next section shows exact results in the fraction form. After this in the next section, the decimal approximation of the result is displayed. Then the other section shows the Repeating decimal in the decimal approximation.
The number line representing the results is displayed in the next section. After this, the Egyptian fraction expansion of the result is shown in another section. And the last section displays the alternative representations of the data.
In this way, this calculator displays detailed results for the input values.
How Does the Body Type Calculator Work?
The Hypergeometric calculator works by determining the hypergeometric distribution of the variable or event. For this it uses a specific formula hence, it needs some input values like population, successes, etc. to get the results.
An understanding of the hypergeometric distribution and the related terms used in this calculator is important. So the brief description is mentioned in the next section.
What Is Hypergeometric Distribution?
A hypergeometric distribution is the probability of success in an event or experiment in which the objects are selected without any replacement. If an object is selected, it can not be replaced with any other object of the group.
The hypergeometric distribution is applicable for the finite number of populations without any replacement of objects and the trials are dependent.
This distribution is very similar to the binomial distribution but both have different properties and formulae but the core concept and basic mathematics have the same grounds.
The formula for Hypergeometric Distribution
The calculator uses the following formula for calculating the results:
\[ P(X=x) = \frac{\dbinom{K}{x} \dbinom{N-K}{n-x}}{\dbinom{N}{n}}\]
Whereas;
N = the total number of items in the population
K = the number of success in the population
n =the sample size
x = the number of successes in the sample
What Is the Population Size?
Population size is the set of the total number of objects or items in a finite population from which items are selected randomly. For example, 8 cards are picked from a deck of 52 cards in a game. In this case, 52 will be the population size.
What Is the Sample Size?
The sample size is the set of total items that are randomly selected from a finite population. For example, 8 cards are picked from a deck of 52 cards in a game. In this case, 8 will be the sample size.
What Is the Number of Successes?
The number of successes is the count of the successes in an event. Each element in the population can be either a success or a failure, true or false, etc.
Thus, the count of successes in a sample is called the number of successes in the sample and the count of successes in the population is called the number of successes in the population.
Solved Examples
A good way to understand the tool is to solve the examples using it and analyze those examples. So, some examples are solved using the hypergeometric calculator.
Example 1
The Father of Harry and Joy bought a pack of chocolates which contains 12 dark and 26 white chocolates. Father asked Harry to close his eyes and pick 10 chocolates from the pack.
The father applied a condition that has to pick them up in a single attempt, there shall be no replacement. Find the probability that Harry has picked exactly 4 dark chocolates.
Solution
The following parameters shall be given to the calculator as input
N = 48
K = 12
n = 10
x = 4
Now, the calculator applies the formula for Hypergeometric Distribution:
\[ P(X=4) = \frac{\dbinom{12}{4} \dbinom{48-12}{10-4}}{\dbinom{48}{10}}\]
The calculator displays this in the first section under the heading Input
Now, it simplifies the equation as follows:
P(X = 4) = 12!*36!*10!*38! / (48!*4!*8!*6!*30!)
= 3652110 / 24775439
This result is shown under the heading Exact Fraction.
In the next step, the calculator displays the fraction in decimal form under the heading Decimal approximation as follows
P(X=4) = 0.14740848789803482392380615333…
The next section displays the repetition of decimals under the heading Repeating Decimal:
(period 53 130)
Now, in the next section, it displays a number line representing the result.
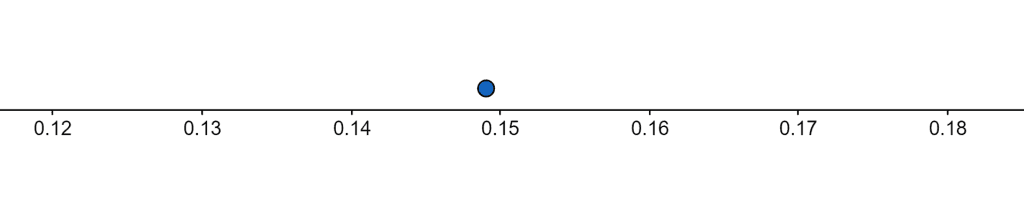
Figure 1
Example 2
Two friends are playing cards. The deck contains a total of 52 cards out of which 26 are black and 26 are red. One of the friends picks 8 cards in his turn.
Find the probability that he has pickup up exactly 6 red cards from the deck under the condition that there is no replacement.
Solution
The following parameters shall be given to the calculator as input
N = 52
K = 26
n = 8
x = 6
Now, the calculator applies the formula for Hypergeometric Distribution:
\[ P(X=6) = \frac{\dbinom{26}{6} \dbinom{52-26}{8-6}}{\dbinom{52}{8}}\]
The calculator displays this in the first section under the heading Input
Now, it simplifies the equation as follows:
P(X = 6) =715 / 7191
This result is shown under the heading Exact Fraction.
In the next step, the calculator displays the fraction in the decimal form under the heading Decimal approximation as follows
P(X=4) = 0.0994298428591294673…
The next section displays the repetition of decimals under the heading Repeating Decimal:
P(X=4) = 0.0994298428591294673…
(period 368)
Now, in the next section, it displays a number line representing the result.
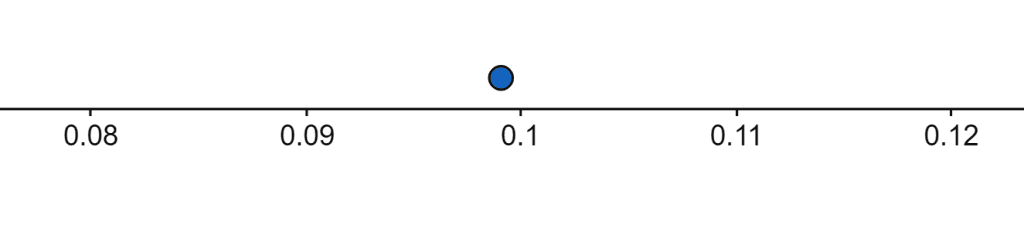
Figure 2
All the mathematical images/graphs are created using GeoGebra
