JUMP TO TOPIC
Inequality Calculator + Online Solver With Free Steps
The Inequality Calculator is a tool used to calculate the interval of the unknown variable in a linear inequality.
The calculator takes the mathematical expression for the inequality as input and in return, it finds the interval notation and number line representation with an inequalities plot.

What Is the Inequality Calculator?
The Inequality Calculator is an online calculator that allows you to determine the intervals for linear inequality problems.
Linear Inequality is an expression that uses symbols of inequality to perform a comparison between two algebraic terms. It is easy to solve these inequalities manually but for this, you need to use basic mathematical techniques and do some calculations.
Therefore we offer you this advanced Inequality Calculator that can solve any kind of linear equality within a few seconds. You only need to enter the inequality; there is no need to perform any maths.
Mathematicians and students can deal with linear equality problems without any hassle using this powerful tool. Unlike other modern tools, you don’t need to buy a subscription for using it.
This calculator is entirely free and can be accessed 24/7 with any appropriate browser. It is an effective and reliable tool because it provides the perfect solutions for your problem.
We are confronted with linear inequalities almost every day. It is mainly used in finding ranges of a parameter like maximum transaction from debit card, area of a field, calculating speed limits, persons in a lift, etc.
To know further information about the procedure and working mechanism of the calculator you may refer to the next sections.
How To Use the Linear Inequality Calculator?
To Use the Inequality Calculator, we plug in the expression of inequality required by the calculator.
The calculator’s front end consists of an empty box for the input and a click-button for acquiring the solution. This tool is simple enough for anyone to use. It can handle only one linear inequality at a time.
You must follow the given detailed guidelines, and the calculator will surely provide you with the desired results.
Step 1
Enter the linear equality in the given space. Make sure to use the correct signs of inequality according to your problem.
Step 2
After entering the expression, press the “Submit” button to start the computation.
Output
The calculator gives the solution to the problem in several steps. In the first step, it gives the input information where the user can once again validate the input.
Then the inequality plot is shown. Here, the two sides of an inequality are considered as separate terms and their respective graphs are plotted.
It gives the solution to the inequality and the proper notation of the interval for the unknown variable. Also, it provides the various alternate forms of the obtained interval.
In addition to these solutions, the calculator has an additional feature of number line representation that allows users to visualize the obtained interval in a single plane of the variable.
How Does the Inequality Calculator Work?
The inequality calculator works by solving the linear inequalities and finding its solution for the required variables. It also provides the inequality graph and its solution on the number line.
The appropriate use of this inequality calculator can be made possible when there is knowledge about inequality and its types.
What Is an Inequality?
Inequalities are mathematical expressions that are not equal on both sides. It is the relationship of expression which have a non-equal comparison.
The equal sign in between the equation is replaced by greater than, greater than or equal to, less than, less than, or equal to sign.
There are different types of inequalities such as Polynomial inequalities, Absolute value inequalities, and Rational inequalities.
Polynomial Inequalities
Polynomial inequalities contain polynomials on both sides of the inequality. Polynomial inequalities are further divided into different types but the most important ones are Linear inequalities and Quadratic inequalities.
This calculator focuses on solving linear inequalities therefore the explanation and method of solving linear inequalities are given below.
Linear Inequalities
The algebraic inequality in which two linear polynomials are compared using the inequality symbols is known as linear inequality. The expression on both sides of inequality must be a polynomial having the highest power equal to one.
Rules of Inequalities
The four basic arithmetic operators are applied to linear inequalities for solving them. However, there are some rules for these operators that should know before using them.
Addition Rule
The addition rule states that when a number is added on both sides of inequality there is no change in the inequality symbol. For instance, adding a number in the inequality ‘x < y’ results in ‘x+a < y+a’.
Subtraction Rule
When a constant is subtracted from the inequality, the inequality sign does not change according to the subtraction rule. If there is inequality such as ‘z > x’ then after subtracting a number it gives ‘z-b > x-b’.
Multiplication Rule
The multiplication rule changes the inequality symbol according to the positive or negative number that is multiplied. If the positive number is multiplied on both sides of an inequality, the symbol does not change.
Whereas, multiplication with a negative number results in a change of the inequality symbol. For example, the inequality ‘y > z’ when multiplied by the negative constant ‘a < 0’ gives ‘y*a < z*a’.
Division Rule
The division rule implies that the inequality symbol does not change when there is a division of positive numbers. However, when a negative number is divided into both sides of inequality, then the symbol is reversed.
If the inequality ‘x < y’ is divided by a negative constant ‘c < 0’ then it results in ‘(x/c) > (y/c)’.
Solving the Linear Inequality
The linear inequalities can be solved by simplifying the inequalities expressions for the required variables. The above-mentioned rules for basic operators should be followed while solving these inequalities.
If it is required to find the solution, first write the inequality as an equation and then solve the equation for the desired variable and obtain the required value.
The solution for the variable is less than or greater than the obtained value if there is a strict inequality. Whereas the solution is less than or equal to or greater than or equal to the value when there is not a strict inequality.
Finally represent the solution on the number line. Then draw the open dot at the endpoint for the excluded value of the solution and for the included value draw the closed dot.
Linear Inequality With Two Variables
Linear inequalities in two variables show the inequality between two algebraic expressions that involve distinct variables. The solution to these inequalities is the values of ‘x’ and ‘y’ usually written in ordered pairs as (x,y).
These ordered pairs contain those values for which the given inequality stands true for both variables. The linear inequality in two variables is solved in the same manner as it is solved in one variable and according to the rules for basic arithmetic operators.
Solved Examples
In order to understand the working of the tool, we need to solve some problems and analyze their result. So let’s review the problems solved by this exceptional tool.
Example 1
Tyler wants to buy a suit of cost $185. He has a total savings of $31 and he earns $7 per hour from his job. Calculate the number of hours he has to work to collect the amount equal to the price of the suit.
This problem can be written in the form of expression as follows:
7h + 31 $\ge$ 185
Here the variable is hours and is represented as ‘h.’
Solution
The solution to the above problem by the calculator is given below.
Inequality Plot
Figure 1 shows the plot for the inequality in the x-y plane.
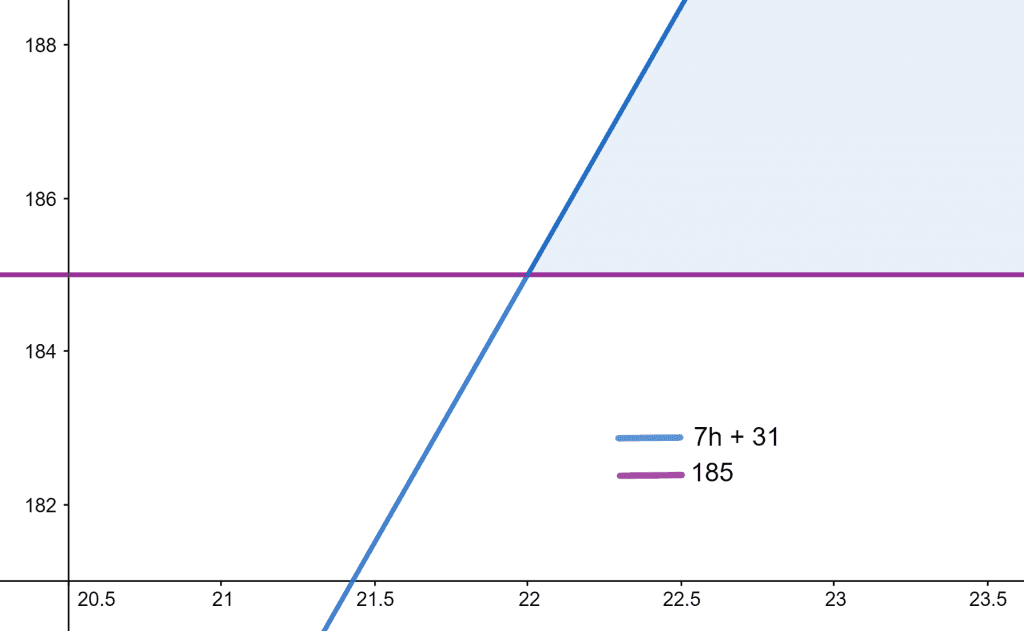
Figure 1
Result
After solving the inequality, some values from the obtained interval of the unknown variable are given below.
h = 22, h = 23, h = 24, h = 25
Interval Notation
The proper notation for the interval of the unknown variable ‘h’ is given below:
[ 22, + $\infty$)
Alternate Form
The solution can also be written in the form of inequality.
h $\ge$ 22
So Tyler has to work for at least 22 hours to buy the suit.
Number Line
The interval can be plotted in a single plane for better understanding which is shown in figure 2.

Figure 2
Example 2
A maths student appears in an exam. He is asked to solve the following inequality and find the proper interval notation for the variable ‘x.’
– 3x – 7 < x + 9
Solution
According to the given expression, the calculator gives the following answer.
Inequality Plot
Both algebraic terms of inequality are separately drawn as a line in the cartesian plane in figure 3.
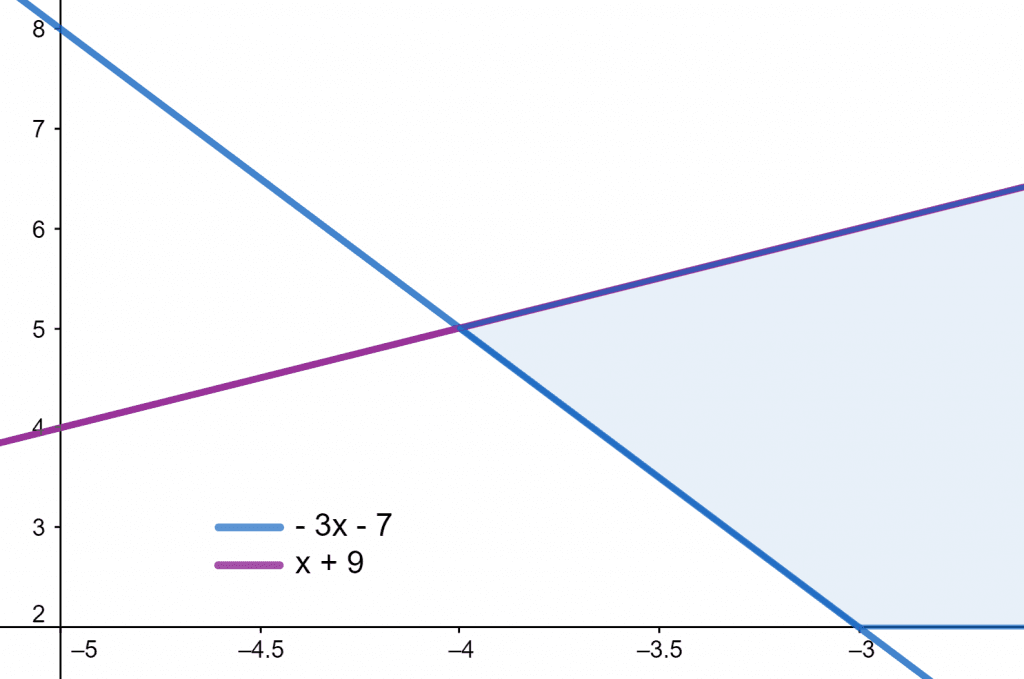
Figure 3
Result
The solution for variable ‘x’ is given as:
x > – 4
Interval Notation
The interval notation is provided below.
(- 4, – $\infty$)
Alternate Form
The alternate form for the resultant interval are given below:
x > – 4
x + 4 > 0
Number Line
Figure 4 illustrates the interval as a number line.

Figure 4
