JUMP TO TOPIC
Smart Calculator + Online Solver With Free Steps
The online Smart Calculator is a calculator that takes different types of equations and finds the results.
The Smart Calculator is a powerful tool that professionals and students can use to solve different complex equations quickly.

What Is a Smart Calculator?
A Smart Calculator is an online calculator that allows you to input different types of equations, providing you with instant results for them.
The Smart Calculator only requires a single input or equation, and the calculator analysis and solves the equation accordingly.
How To Use a Smart Calculator?
To use the Smart Calculator, we only need to input the equation and click the “Submit” button. The calculator instantly finds the results and displays them in a separate window.
Here are some detailed instructions on how to use the Smart Calculator:
Step 1
In the first step, we enter the equation given to us into the Smart Calculator.
Step 2
After entering the equation in the Smart Calculator, we click the “Submit” button. The calculator quickly performs the calculation and displays them in a new window.
How Does a Smart Calculator Work?
The Smart Calculator works by taking a complex equation as input and solving it quickly. The Smart Calculator analyzes the equation and determines what type of equation is provided to the calculator. After choosing the type of equation, the Smart Calculator solves the equation accordingly.
The Smart Calculator can solve several different equations, including:
- Linear Equations
- Quadratic Equations
- Cubic Equations
- Higher Degree Polynomials
What Is a Linear Equation?
A linear equation is an equation in which the variable’s maximum power is consistently one. Another name for it is a one-degree equation. A linear equation with one variable has the conventional form Ax + B = 0. In this case, the variables x and A are variables, while B is a constant.
A linear equation with two variables has the conventional form Ax + By = C. Here, the variables x and y, the coefficients A and B, and the constant C are all present.
This equation always produces a straight line when it is graphed. It is called a “linear equation” for this reason.
The following equation is an example of linear equations:
y= 3x – 3
What Is a Quadratic Equation?
A quadratic equation is an algebraic equation of the second degree in x and is written as $ax^{2} + bx + c = 0$, where a and b are the coefficients, x is the variable, and c is the constant term.
A non-zero term (a $\neq$ 0) for the coefficient of $x^{2}$ is a prerequisite for an equation to be a quadratic equation. The $x^{2}$ term is written first, then the x term, and finally, the constant term is written when constructing a quadratic equation in standard form. The numerical values of a, b, and c are typically expressed as integral values rather than fractions or decimals.
The following equation is an example of a quadratic equation:
\[ 4x^{2} + 4x – 2 = 0 \]
When a quadratic equation is solved, the two values of x that result are known as the roots of the equation. The zeros in the equation are another name for these quadratic equation roots.
What Is a Cubic Equation?
A cubic equation is a polynomial equation with the greatest exponent of three and is commonly used to calculate volumes, but they have many more uses after you study more advanced mathematics, such as calculus. In the 20th century BC, the ancient Babylonians were the first known humans to apply the cubic equation.
The general cubic equation formula is $ax^{3} + bx^{2} + cx + d=0$, where each equation variable is a real number and a $\neq$ 0. This is also known as the cubic equation’s standard form.
The variable’s exponents must be in decreasing order in standard form, and all terms must be on one side of the equation. A cubic equation is illustrated below:
\[ 7x^{3} + 5x^{2} + 2x + 4 \]
Solved Examples
The Smart Calculator quickly analyzes the type of equation used and calculates the results instantly.
Here are some examples solved using the Smart Calculator:
Example 1
While working on his homework, a high school student comes across the following equation:
\[ 4x^{2} + 5x = 0 \]
To complete his homework, the student needs to solve this equation. Using the Smart Calculator solve the equation to find the answer.
Solution
We can use the Smart Calculator to find the equation’s result instantly. First, you need to enter the given equation into the Smart Calculator; the given equation is $4x^{2} + 5x = 0$.
After entering the equation into its respective box, we click the “Submit” button on the Smart Calculator. The calculator quickly displays the results in a separate window.
The following results are generated using the Smart Calculator:
Input:
\[ 4x^{2} + 5x = 0 \]
Root Plot:
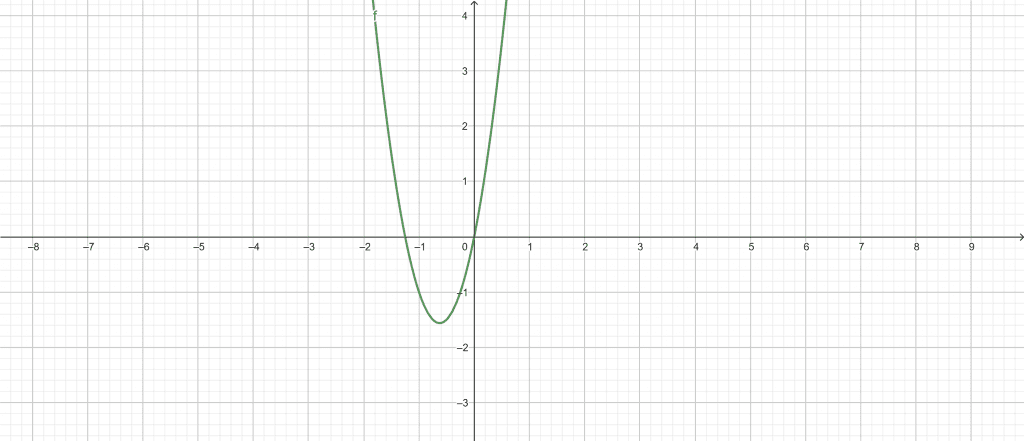
Figure 1
Alternate Forms:
x(4x + 5) = 0
\[ 4(x+\frac{5}{8})^{2}-\frac{25}{16}=0\]
Number Line:
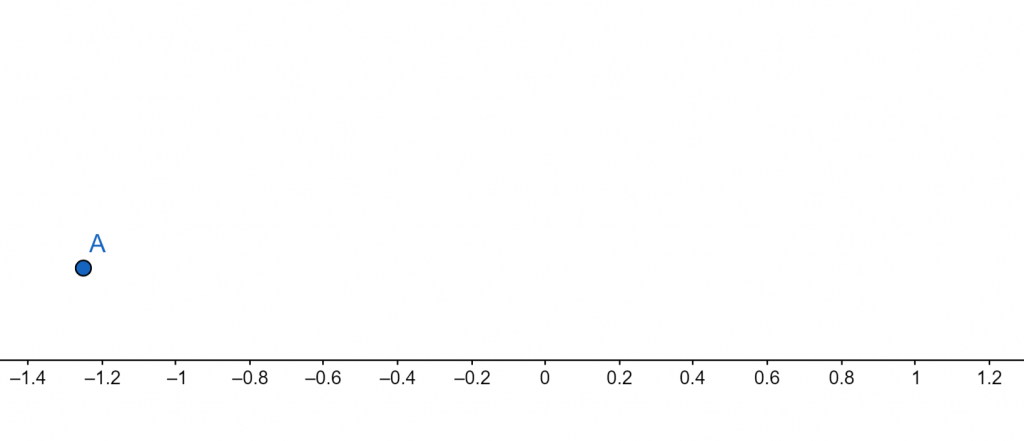
Figure 2
Solutions:
\[ x = -\frac{5}{4} \]
x = 0
Sum of Roots:
\[ -\frac{5}{4} \]
Product of Roots:
0
Example 2
During his research, a mathematician comes across the following equation:
\[ 13x^{2} + 3x + 4\]
To complete his research, the mathematician needs to solve this equation. With the Smart Calculator’s help, solve the equation given above.
Solution
We can utilize the Smart Calculator to determine the equation’s solution quickly. To begin, insert the given equation into the Smart Calculator; the given equation is $13x^{2} + 3x + 4$.
After typing the equation into the appropriate field, we use the Smart Calculator to click the “Submit” button. The calculator presents the results in a different window rapidly.
The Smart Calculator produces the following results:
Input:
\[ 13x^{2} + 3x + 4\]
Plot:
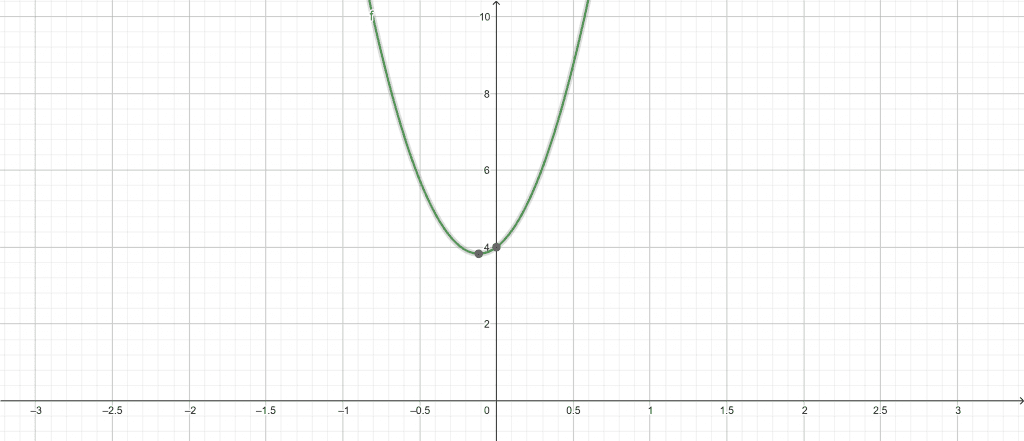
Figure 3
Geometric Figure:
Parabola
Alternative Forms:
x(13x + 3) + 4
\[ 13(x+\frac{3}{26})^{2} + \frac{199}{52} \]
\[ \frac{1}{52}(26x + 3)^{2} + \frac{199}{52} \]
Polynomial Discriminant:
\[ \Delta = -199 \]
Derivative:
\[ \frac{d}{dx}(13x^{2} + 3x + 4) = 26x + 3 \]
Indefinite Integral:
\[ \int (13x^{2} + 3x + 4)dx = \frac{13x^{3}}{3} + \frac{3x^{2}}{2} + 4x + \text{constant} \]
Example 3
While experimenting, a scientist needs to calculate the following equation:
\[ \sin^{2}{x} + \sin{x} – 5 \]
With the help of the Smart Calculator, solve the equation.
Solution
We can use the Smart Calculator to determine the equation’s solution quickly. First, enter the supplied equation into the Smart Calculator; the given equation is sin (x).
After entering the equation into their respective area on the Smart Calculator, we press the “Submit” button. The calculator instantly displays the findings in a different window.
The Smart Calculator yields the following results:
Input:
\[ \sin^{2}{x} + \sin{x} – 5 \]
Plots:
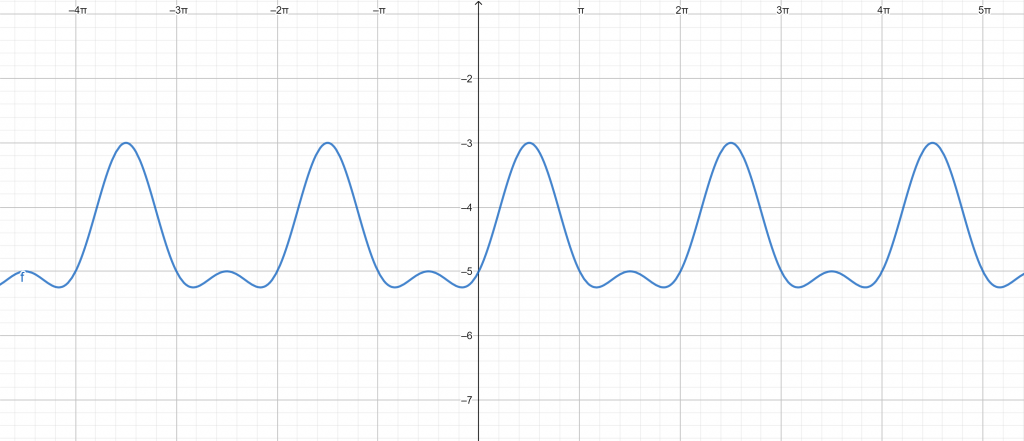
Figure 4
Alternate Forms:
\[ \sin{(x)} – \cos^{2}{(x)} – 4 \]
\[ \frac{1}{2}(2\sin{(x) – 2\cos{(2x) – 9}}) \]
\[ \frac{1}{2}i e^{-i x}-\frac{1}{2}i e^{i x} – \frac{1}{4}i e^{-2i x} – \frac{1}{4}i e^{2i x} – \frac{9}{2} \]
Domain:
\[ \mathbb{R} \]
Range:
\[ \left \{ y \in \mathbb{R}: – \frac{21}{4}\leq y \leq -3 \right \} \]
Derivative:
\[ \frac{d}{dx}\sin^{2}{(x)} + \sin{(x)} – 5 = (2\sin{(x) + 1}) \cos{(x)}) \]
Indefinite Integral:
\[ \int \sin^{2}{(x)} + \sin{(x)} – 5 = -\frac{9x}{2} – \frac{1}{4}\sin{(2x)} – \cos{(x)} + \text{constant} \]
All Images/Graphs are made using GeoGebra.
