Reflection in Geometry – Explanation, and Examples
 A reflection in geometry is the transformation of an object by creating a mirror image of it on the other side of a given line.
A reflection in geometry is the transformation of an object by creating a mirror image of it on the other side of a given line.
Often, this line is the x-axis, y-axis, or the line $y=x$.
Before moving on, make sure to review math transformations and coordinate geometry.
This topic covers:
- What is a Reflection in Geometry?
- How to Do Geometric Reflections
- Geometry Reflection Definition
What is a Reflection in Geometry?
A reflection in geometry is a mirror image of a function or object over a given line in the plane. The most frequently used lines are the y-axis, the x-axis, and the line $y=x$, though any straight line will technically work.
A reflection reverses the object’s orientation relative to the given line. The final figure will be an equal distance from the line as the preimage but on the opposite side. If the original figure is close to the line, the reflected figure will also be close to the line. If the original figure is further from the line, the reflected figure will also be further from the line.
Put another way, the midpoint between any two corresponding points in the original image and the reflected image lies on the line of reflection.
To visualize the reflected version of an object, imagine a cut-out of the object sitting on a table. If you pick up the original and flip it over onto the backside while moving it over the given line, you will have the reflected version’s orientation.
The Line of Reflection
Any line can be a line of reflection, but the axes and the line through the origin with slope 1 are most common.
Note that we can use more than one line in a series of reflections. For example, you can reflect an object over the x-axis and then the y-axis.
What happens when an object passes through the given line?
In that case, the two sides of the object are treated separately. Reflect the part on the right to the left of the line, and then reflect the part on the left of the line onto the right side.
Any function that passes through the y-axis and maps to itself when reflected over the y-axis is an even function. Put another way, even functions are symmetric about the y-axis.
If a function that passes through the origin maps onto itself after being reflected over the y-axis and the x-axis, it is an odd function.
How to Do Geometric Reflections
Geometric reflections about the axes or other vertical and horizontal lines are simpler than reflections about other lines.
As with other types of transformations, find the coordinates of key points for the function or object and transform those. Then, “connect the dots” to complete the figure.
Reflection about the y-axis
A reflection about the y-axis changes the sign of each of the x-values of a figure’s coordinates. That is:
$(x, y) → (-x, y)$.
Reflection about the x-axis
A reflection about the x-axis changes the sign of each of the y-values of a figure’s coordinates. That is:
$(x, y) → (x, -y)$.
Other Horizontal and Vertical Lines
The easiest way to do a reflection about another horizontal or vertical line is to:
- Draw the line
- Consider the line and original object as one figure.
- Translate the entire figure to the line of reflection maps to the x-axis (for horizontal lines) or y-axis (for vertical lines).
- Reflect the original object over the axes.
- Undo the translation from step 3. That is, if you translated the figure 4 units right, translate the figure 4 units left.
Other Lines of Reflection
Other lines of reflection are more complicated. This is a situation where construction with a compass and ruler helps in coordinate geometry.
First, create a line from each key point in the figure that meets the reflection line at a right angle. Then, extend this line so that the intersection point with the line of reflection is the midpoint. The other endpoint of this line is the corresponding point in the reflection.
Example 4 covers this in greater detail.
Geometry Reflection Definition
A reflection is a transformation that casts a mirror image of a given object over a given line.
Examples
This section covers common examples of problems involving math reflections and their step-by-step solutions.
Example 1
The line segment AB maps to CD through a reflection. What is the line of reflection?
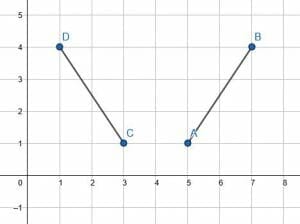
Example 1 Solution
First, to find the line of reflection, connect the key points to their corresponding point in the reflected figure. In this case, connect CA and DB.
Then, find the midpoints of each of these segments. Call them E and F.
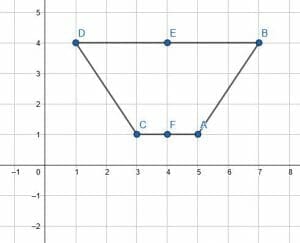
Then, connect the midpoints to find the line of reflection. In this case, the line connecting E and F is the vertical line $x=4$.
Example 2
Reflect the given object over the x-axis.
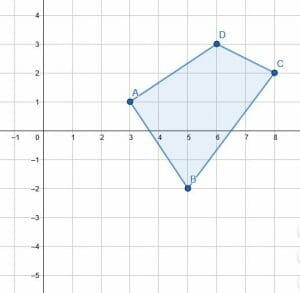
Example 2 Solution
Note that the points on the x-axis will map to themselves.
Since this is a reflection over the x-axis, we first need to find the coordinates of the figure’s vertices. These are (3, 1), (5, -2), (8, 2), and (6, 3).
Then, to find the corresponding points in the reflected figure, change the sign value of the y-coordinate of each point. This makes A’ (3, -1), B’ (5, 2), C’ (8, -2), and D’ (6, -3). Then, connect the figure A’B’C’D’ to complete the reflection.
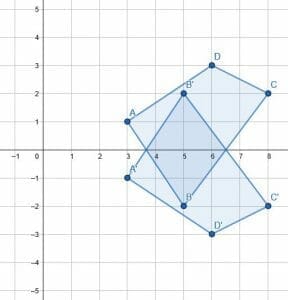
Example 3
Reflect the given function over the y-axis. Is the function even?
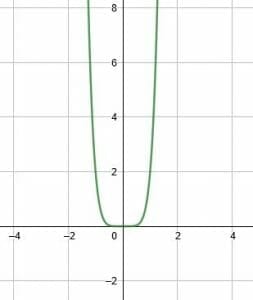
Example 3 Solution
This function passes through the y-axis and the point (0, 0). It also passes through the points (1, 2) and (-1, 2).
The reflection of the point (1, 2) over the y-axis makes the x-coordinate negative. That is, the reflection is (-1, 2), which is also a point on the function. Likewise, (-1, 2) maps to (1, 2).
Therefore, the function maps to itself when reflected over the y-axis. By definition, therefore, it is an even function.
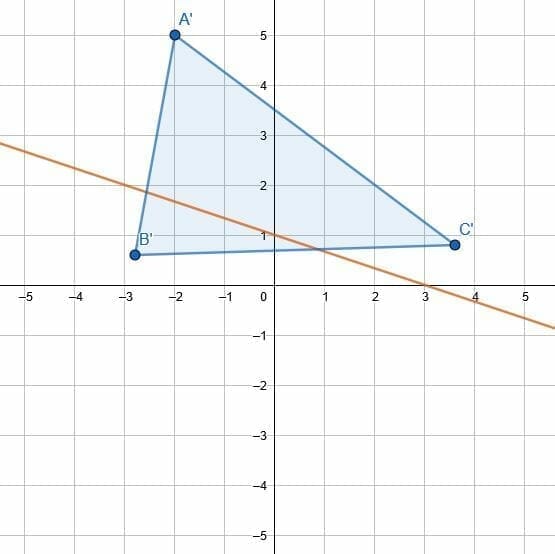
Example 4
Reflect the given triangle over the given line.
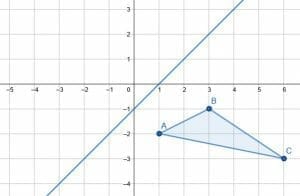
Example 4 Solution
To reflect over a non-vertical or non-horizontal line, create a line segment from each triangle’s vertex to the given line. In particular, these line segments should meet the given line at right angles.
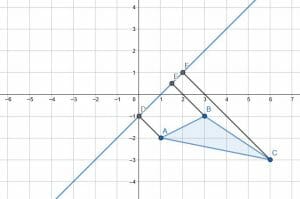
Then, extend these lines to new points so that D, E, and F are the new line segments’ center. We can do this by extending the lines with a ruler. Then, create circles with center F and radius FC, center E and radius EB, and center D and radius DA.
The intersection of the extended lines with these circles gives us the reflected vertices. Then, connect these vertices to complete the reflection.
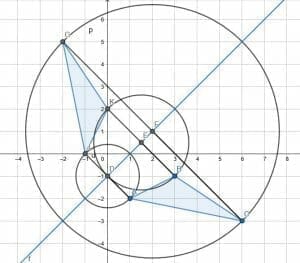
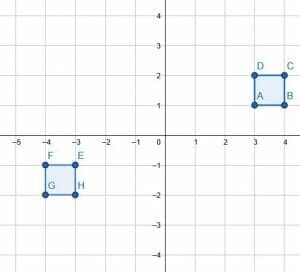
Example 5
Reflect the square over the y-axis and the x-axis.
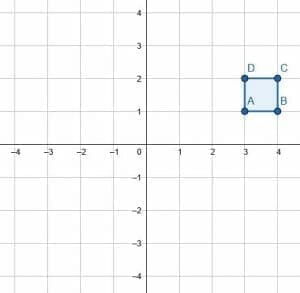
Example 5 Solution
Note that the order of reflections does not matter. The image will be the same if you first reflect over the x-axis and then the y-axis or reflect over the y-axis and then the x-axis.
Note that since the square has vertical and horizontal lines of symmetry, it will stay the same when reflected over a vertical or a horizontal line.
The original coordinates are (3, 1), (4, 1), (4, 2), and (3, 2). Since the object is reflected over both axes, both the x and y coordinates will change signs. Therefore, the coordinates of the reflection are (-3, -1), (-4, -1), (-4, -2), and (-3, -2).
Practice Questions
![]()
Open Problems
1. Reflect the function over the x-axis and the y-axis.
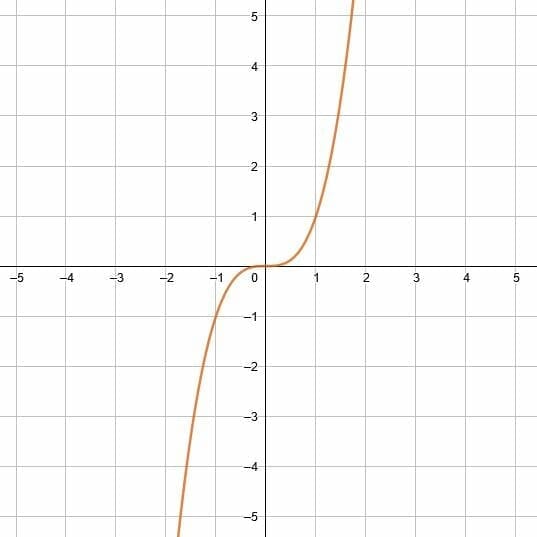
2. Reflect the given object over the given line.
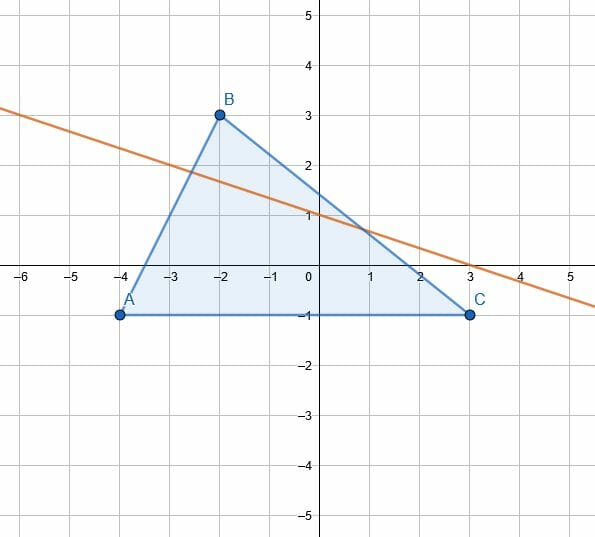
Open Problem Solutions
1.

2.
Images/mathematical drawings are created with GeoGebra.
