Reflex Angle – Explanation and Examples

A reflex angle is an angle greater than a straight angle and less than a circle.

In degrees, a reflex angle measures greater than $180$ degrees and less than $360$ degrees. In radians, a reflex angle measures greater than $\pi$ radians and less than $2\pi$ radians.

Reflex angles, like other types of angles, are important in many areas of science, mathematics, and engineering.

Before moving on with this section, read over angles and types of angles.

This section covers:

• What is Reflex Angle?
• Reflex Angle Definition
• Reflex Angle Examples

What is Reflex Angle?

A reflex angle is an angle greater than a straight angle but less than a circle.

These angles have measures between $180$ and $360$ degrees not inclusive or between $\pi$ and $2\pi$ radians not inclusive.

Sometimes, obtuse angles are defined as any angle greater than a right angle, $90$ degrees, or $\frac{\pi}{2}$. But, a more precise definition specifies that an obtuse angle is also less than a straight angle. That is, it must be less than $180$ degrees or $\pi$ radians.

For this reason, reflex angles may occasionally be categorized as obtuse angles or as a special type of obtuse angle. It is more precise, however, to categorize them as a separate type of angle entirely.

To imagine a reflex angle, picture any acute or obtuse angle.

Then, instead of measuring that angle, measure the wider angle formed by the rays. This will be a reflex angle.

Concave Figures

Recall that a polygon is any closed figure made of only straight lines.

A convex polygon is a polygon whose interior angles are all less than a straight angle but greater than a zero angle. That is, all of the interior angles will be acute or obtuse.

A concave polygon, however, has at least one reflex angle

Reflex Angle Definition

A reflex angle is an angle that is larger than a straight angle but smaller than a circle.

For any reflex angle $\alpha$ the following are true.

$180 < \alpha < 360$ when $\alpha$ is measured in degrees.

$\pi < \alpha < 360$ when $\alpha$ is measured in radians.

Reflex Angle Examples

Some examples of the measures of reflex angles in degrees are:

• $180.0001$ degrees
• $200$ degrees
• $270$ degrees
• $300$ degrees
• $359.999$ degrees

Some examples of the measure of reflex angles in radians are:

• $\frac{101}{100} \pi$ radians
• $\frac{6}{5} \pi$ radians
• $\frac{3}{2} \pi$ radians
• $\frac{15}{8} \pi$ radians
• $\frac{199}{100} \pi$ radians

Common Examples

This section covers common examples of problems involving reflex angles and their step-by-step solutions.

Example 1

Prove that the external angles of a triangle are always reflex angles.

(Clarification: external angle here refers to the angle outside the vertex of the triangle)

Solution

The exterior angles of a triangle are the angles of the triangle measured in the opposite direction. They are the larger angles that lie outside the triangle.

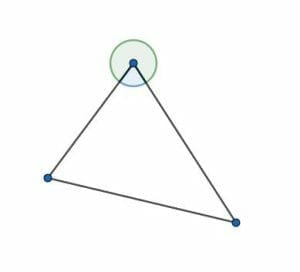
In the above illustration, the green angle is the exterior angle and the blue angle is the interior angle.

Note that the two angles, together, make a complete circle. Additionally, recall that the sum of the interior angles of a triangle is $180$ degrees and that each angle inside a triangle is greater than the zero angle.

If three angles with measures, $a$, $b$, and $c$ add up to $180$ degrees and each is greater than the zero angle, $0 < a < 180$, $0 < b < 180$, and $0 < c < 180$. In radians, $0 < a < \pi$, $0 < b < \pi$ and $0 < c < \pi$ radians.

Then the measure of the exterior of each of these angles will be $360-a$, $360-b$, and $360-c$. Because of the above inequalities, however, $360-0 > 360-a > 360-180$. That is, $360 > a > 180$ degrees. Similarly, $360 > b > 180$ degrees and $360 > c > 180$ degrees.

Thus, all three of these exterior angles are between $180$ degrees and $360$ degrees not inclusive. By definition, these angles are reflex angles.

Example 2

Find the sum of the external angles of a triangle.

(Clarification: external angle here refers to the angle outside the vertex of the triangle)

Solution

As shown above, an interior angle and an exterior angle measured together make a circle.

In degrees, a circle has $360$ degrees. Since the interior angle and its corresponding exterior angle will make a circle for each of the triangle’s three angles, the total of the interior angles plus the exterior angles will be three circles, or $360\times3 =  1080$ degrees

Additionally, it is known that the interior angles of a triangle measure $180$ degrees.

Therefore, the sum of the exterior angles will be $1080-180 = 900$ degrees. This is equivalent to two and a half circles.

In radians, this is $6\pi – \pi = 5\pi$.

Example 3

Prove that the sum of an obtuse angle and a right angle will always be a reflex angle.

Solution

Like the previous problem, this reflex angle example uses inequalities to show that a given angle’s measure is between the measure of a straight angle and the measure of a circle.

In this case, the measure of the right angle in degrees is $90$ degrees. Such an angle has a measure of \frac{\pi}{2}$ radians.

The measure of the obtuse angle will be between the measure of a right angle and a straight angle not inclusive. In degrees, its measure will be greater than $90$ degrees and less than $180$ degrees. In radians, its measure will be between $\frac{\pi}{2}$ radians and $\pi$ radians not inclusive.

Let $\alpha$ be the measure of the right and obtuse angle together. Therefore, $\alpha$ will be greater than two right angles and less than a straight line plus a right angle. In degrees, its measure will be strictly greater than $180$ degrees and less than $270$ degrees. In radians, its measure will be greater than $\pi$ radians and less than $\frac{3\pi}{2}$ radians.

Since a reflex angle has a measure greater than $180$ degrees but less than $360$ degrees or greater than $\pi$ radians and less than $2\pi$ radians, the angle $\alpha$ will be a reflex angle.

Example 4

Is there an angle supplement for a reflex angle? If so, what is it?

Solution

Whether or not there is an angle supplement for a reflex angle depends on the system being used.

Why?

Some systems use negative angles. For example, a positive angle on a unit circle used in most trigonometry systems is measured counterclockwise while a negative angle is measured clockwise. Generally, negative angles are used to denote a certain orientation in space and to graph functions that have angles as inputs.

In such a system, a reflex angle has a supplement. The supplement is the value of $180-\alpha$, where $\alpha$ is the reflex angle. Since $180 < \alpha$ < 360$, the supplementary angle will be between $0$ and $-180$ degrees not inclusive.

In radians, the measure of the supplementary angle will be between $0$ and $-\pi$ radians not inclusive.

Example 5

Prove that the angle $BAD$ is a reflex angle.

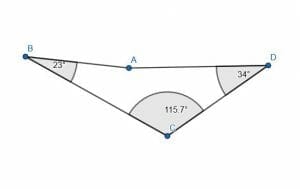
Solution

The angle $BAD$ is one of four angles in the quadrilateral $BADC$. It is known that the interior angles of a quadrilateral measure $360$ degrees. Therefore, the measure of $BAD$ is equal to $360$ minus the sum of the other three angles. Fortunately, these three angles are given.

$115.7+34+23 = 172.7$. Therefore, the measure of the angle $BAD$ must be $360-172.7 =  187.3$ degrees. Since this angle has a measure greater than $180$ degrees and less than $360$ degrees, it is a reflex angle by definition.

More Examples with Explanation

1. Prove that the exterior angles of any convex polygon are reflex angles.
2. Find the total sum of the exterior angles of any n-gon.
3. What kind of angle will two reflex angles create?
4. Prove that a concave quadrilateral has at least two acute angles.
5. Prove that there can be at most $n-3$ concave angles in a concave polygon.

Answer Key

1. Any convex polygon will have only acute or obtuse angles. That is, all of its interior angles will have a measure between $0$ and $180$ degrees not inclusive or between $0$ and $\pi$ radians not inclusive. The sum of an interior angle and its corresponding exterior angle will be a full circle. That is, it will be $360$ degrees or $2\pi$ radians.
   Therefore, if all of the interior angles of a polygon are less than $180$ degrees or $\pi$ radians, the corresponding exterior angles will be greater than $360-180 = 180$ or $2\pi-\pi = \pi$ and less than $360-0 = 360$ or $2\pi-0 = 2\pi$. Thus, their measure will be that of a reflex angle.
2. For any n-gon, the sum of the interior angles will be $180n-360$. The total of the interior and exterior angles of the n-gon will be $360n$, since each interior angle and corresponding exterior angle is $360$ degrees.
   Therefore, the sum of the exterior angles will be the difference $360n-(180n-360) = 180n+360$. That is, the exterior angles will always have a measure total $720$ degrees greater than the interior angle measure total.
3. Such an angle will be greater than the angle of a circle but less than the measure of three straight lines. It will be the equivalent of an acute or an obtuse angle with a circle.
4. A quadrilateral has four angles with an interior angle total of $360$ degrees. Suppose one of those angles was greater than $180$ degrees. The sum of the remaining three angles must therefore be $180$ degrees. Since each angle is greater than $0$, none of the angles can be greater than or equal to $180$ degrees.
   Now, of these three angles, at most one can be greater than or equal to a right angle or $90$ degrees. If there were two angles with a measure greater than or equal to $90$ degrees, they would have a measure greater than or equal to $180$ degrees. This means the third angle would have to be zero degrees or less. Since it must be positive, there must be at least two acute angles in a concave quadrilateral.
5. The interior angle measure of an n-gon is $180n-360$ degrees. The measure of a reflex angle is greater than 180 degrees. Therefore, the total angle measure of the concave angles is greater than $180m$ for $m<n$ concave angles. But, $180m$ must be less than $180n-360$.
   Then, $180m-180n < -360$. Therefore, $-180(n-m) < -360$. Thus, $n-m > 2$. Solving for $m$ yields $n-2 > m$, so $m$ cannot be more than $n-3$, since it must be a whole number.

Images/mathematical objects created with GeoGebra.