JUMP TO TOPIC
Straight Angle – Explanation and Examples
A straight angle is the measure of the inclination of two rays that lie on the same line.
Unlike a zero angle, these two rays will point in opposite directions of the vertex. In degrees, a straight angle measures $180^{\circ}$, and in radians it measures $\pi$ radians.
Straight angles are part of straight lines and play an important role in all areas of mathematics, including geometry, algebra, trigonometry, and calculus. They’re also important in sciences, statistics, engineering, and architecture.
Before moving on with this topic, review angles and their subcategories.
This section includes:
- What is a Straight Angle?
- Straight Angle Definition
- Straight Angle Example
What is a Straight Angle?
A straight angle is an angle that lies on one straight line.
Recall that an angle is the measure of inclination between two rays or line segments that meet at a point. This point is called the vertex.
In the case of a straight angle, the two rays point in opposite directions on a single line.
Typically, an angle is given three points to help identify it. The first point lies on the first ray, the second point is the vertex, and the third point lies on the second ray.
Since the rays of a straight angle lie in a line together, all three points used to name the angle lie on a line. In particular, the middle point (the vertex) will be between the other two points.
Straight Angle vs. Zero Angle
A zero angle also lies on a line, but it is different from a straight angle.
In a zero angle, the two rays that form the angle point in the same direction on the line. The vertex will lie to either the right or the left of the other two points.
In a straight angle, the vertex lies between the two points and the rays point in opposite directions.
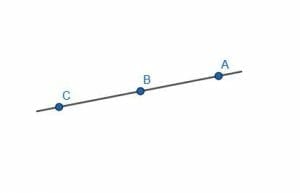
For example, in the given figure, the angles $CAB$, $BAC$, $ACB$, and $BCA$ are zero angles because in each case the vertex is on the same side of the other two points. In the first two angles, the vertex $A$ is to the right of $B$ and $C$. In the second two angles, $C$ is to the left of $B$ and $A$.
However, the angles $CBA$ and $ABC$ are straight angles. This is because the vertex, $B$, lies between other two points $A$ and $C$ which both lie on the same line as $B$.
Additionally, when something makes turns the zero angle, it doesn’t move. When something turns in a straight angle, it turns the exact opposite direction. This is why the expression “make a $180$” means to turn around or completely change opinion.
Straight Angle Definition
A straight angle is the measure of an angle that opens up along a straight line. I measures $180$ degrees or $\pi$ radians.
The two rays that form a straight angle point in opposite directions along the same line.
When three points are used to name a straight angle, all three points will lie on the same line, and the vertex will lie between the other two points.
Straight Angle Example
A circle contains $360$ degrees.
Now, consider the diameter of a circle. It is a straight line that stretches across a circle.
Since the diameter cuts the circle in half through the center, the measure of the upper side of the diameter is $180$ degrees and the measure of the lower side of the diameter is $180$ degrees.
That is, the diameter, as a straight line, forms a straight angle.
Consequently, the arc length of each semicircle formed by the diameter is also $180$ degrees.
Common Examples
This section covers common examples of problems involving straight angles and their step-by-step solutions.
Example 1
Identify all of the straight angles on the given figure.
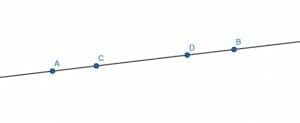
Use the three angle naming system where the first point lies on the first ray, the middle point is the vertex, and the third point lies on the second ray.
Solution
The straight angles in the figure are all of the angles where the vertex lies between the the other two points used to name the angle.
Since $A$ and $B$ don’t have any points to their left and right respectively, they cannot be the vertex of any straight angle.
Instead, $C$ and $D$ must be the vertices.
Therefore, all of the straight angles in the figure are:
- $ACB$ and $BCA$
- $ADB$ and $BDA$
- $ACD$ and $DCA$
- $CDB$ and $BDC$
Note, however, that the angles $ADB$ and $CDB$ are the same along with the angles $BDA$ and $BDC$ because $A$ and $C$ are two points on the same ray. For the a similar reason, the pairs $ACD$ and $ACB$ and $DCA$ and $BCA$ are also the same. In this case, $D$ and $B$ lie on the same ray.
Any angles that double back, such as $ADC$ are not straight angles but instead are zero angles. This is because the two ray points ($A$ and $C$ in this case) lie on the same ray.
Example 2
Find the measure of three straight angles. Give the answer in both radians and degrees.
Solution
It is hard to visualize what three straight angles looks like on the plane.
Instead, think of three straight angles as something that turns in a straight angle three times. What is the total measure of the angle at the end?
If something turns in a straight angle twice, it makes a circle. In the end, it will be back where it started. Then, if it turns another straight angle, it will be facing the exact opposite direction it was facing initially.
The final turn will be $180+180+180 = 540$ degrees or $\pi+\pi+\pi = 3\pi$ radians.
Example 3
Recall that a supplementary angles are two angles that, when added together, total a straight angle.
What angle, then, is the supplementary angle for a straight angle? Answer in both degrees and radians.
Solution
To find the angle supplement’s measure in degrees, subtract the angle measure from $180$. To find the angle supplement’s measure in radians, subtract the angle measure from $\pi$.
In this case, however $180-180 = 0$ and $\pi-\pi = 0$. Therefore, the angle supplement has a measure of $0$ degrees or $0$ radians. It is, consequently, the zero angle.
Similarly, the straight angle is the supplement for the zero angle.
Example 4
What is one-third of a straight angle?
Solution
This question is actually answered with a straightforward application of division.
To find the angle measure, divide the measure of a straight angle by $3$. In degrees, this is $\frac{180}{3} = 60$ degrees. In radians, it is $\frac{\pi}{3}$ radians.
Example 5
In the given figure, $FC$ is a diameter for the circle with center $G$, and $GH$ is a diameter for the circle with center $C$. Additionally, the line $CD$ bisects the angles $GCI$ and the line $DG$ bisects the angle $EGC$. Prove that the angle $EDI is a straight angle.
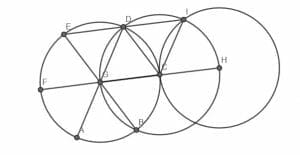
Solution
The main thing to note in this figure is that $DGC$ is an equilateral triangle because the circles with center $G$ and $C$ have the same radius and all three sides are radii of one or both circles.
Since the line $CD$ bisects the angles $GCI$, the angles $GCD$ and $DCI$ are equal.
Then, the triangle $GCD$ is congruent to the triangle $DCI$ by side-angle-side. This is because $CG$, $CD$, and $CI$ are all radii of the same circle, and consequently the same length and the angles $GCD$ and $DCI$ were just proved equal.
Therefore, the third side of each triangle, $DG$ and $DI$, are also equal.
Similarly, since $DG$ bisects $EGC$ and $EG$, $DG$, and $GC$ are radii of the same circle, triangle $DGE$ is congruent to triangle $CGD$.
But, these are equilateral triangles, which also have equal angles. These angles must measure $\frac{180}{3} = 60$ degrees or $\frac{\pi}{3}$ radians. This means that the angles $EDG$, $GDC$, and $CDI$ are all equal and total to a straight line. Thus, the angle $EDI$ is a straight line.
More Examples with Explanation
- Use the fact that a straight angle and a zero both lie on the same line but in opposite directions to make a prediction about how trigonometric functions with the zero angle as an input compare to trigonometric functions with the straight angle as the input.
- Does the straight angle have an angle complement? If so, what is it? If there is a complement, give its measure in radians and degrees.
- Name straight angles on this figure.
- Find measure of $5$ straight angles together.
- $ABCD$ is a parallelogram. Prove that the angle $AEB$ is a straight angle.
Answer Key
- A reasonable prediction is that one output is the negative of the other. This is actually the case.
- It’s complement is a negative right angle. This is equal to $-90$ degrees or $-\frac{\pi}{2}$ radians. In a system with no negative angles, it does not have a complement.
- $ABG$, $GBA$, $CBF$, $FBC$, $EBD$, and $DBE$ are all straight angles.
- To find this, multiple the straight angle by $5$. This angle will have a measure of $900$ degrees or $5\pi$ radians.
- A parallelogram is a quadrilateral. This means that the only sides on the figure are $AC$, $CD$, $DB$, and $BA$. Therefore, the point $E$ must lie on the line $AB$. Otherwise, this would be a five-sided figure instead. Therefore, since $E$ lies on the line $AB$ in between $A$ and $B$, $AEB$ is a straight angle.
Images/mathematical objects created with GeoGebra.
