Tangent Graph – Explanation and Examples

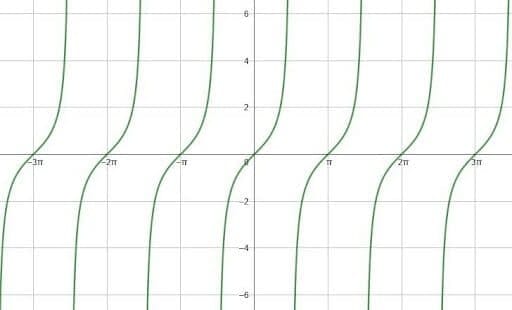
The graph of the tangent function is periodic but discontinuous.

While the sine graph and cosine graphs are continuous and have a wave shape, the tangent graph is undefined at points where cosine is equal to $0$. The tangent graph has applications in electronics, specifically battery eliminator circuits.

Before reading this article, read up on the sine graph and the basics of the tangent function.

How To Graph Tangent

To graph the tangent function, find the value of tangent at major quadrantal angles first. These angles are the angles of the unit circle that lie on the x and y axes. Specifically, they are $0$, $\frac{\pi}{2}$, $\pi$, $\frac{3\pi}{2}$, and all angles coterminal with them.

Since tangent is equal to the sine ratio divided by the cosine ratio, it helps to first consider the values of these functions at the quadrantal angles.

At $0$, sine is $0$ and $cosine$ is $1$. Similarly, at $\pi$ radians, sine is $0$ and cosine is $-1$. In either case, tangent is equal to $0$. But at $\frac{\pi}{2}$ and $\frac{3\pi}{2}$, cosine is equal to $0$. Division by zero is impossible, so the function is undefined here.

Limits of Tangent

What happens as the function gets closer and closer to the angles $\frac{\pi}{2}$ and $\frac{3\pi}{2}$ radians?

The sine of $\frac{\pi}{2}$ is $1$, and the sine is increasing on the interval $(0, \frac{\pi}{2})$. Cosine is positive on this interval and decreases to $0$. This means that the tangent will be positive and will get larger and larger as cosine decreases. Thus, the limit as tangent approaches $\frac{\pi}{2}$ from the right is positive infinity.

After $\frac{\pi}{2}$, the values of sine decrease, and the cosine values also decrease, becoming negative. Therefore, on the left side of $\frac{\pi}{2}$, the tangent function has positive sine values divided by very small cosine values. Thus, the limit as tangent approaches $\frac{\pi}{2}$ from the left is negative infinity.

Similarly, since sine and cosine are both negative in the third quadrant, the limit as tangent approaches $\frac{3\pi}{2}$ from the right is positive infinity. But the limit as tangent approaches it from the left is negative infinity.

Thus, the general shape of the periods in the tangent graph is similar to the shape of the $x^3$ function. They go to negative infinity on the left and positive infinity on the right with a little plateau near the x-axis.

What Is the Period of a Tangent Function?

The period of the tangent function is only $\pi$. This is because the absolute value of sine and cosine repeat over the intervals [-\frac{\pi}{2}, \frac{\pi}{2}] and [\frac{\pi}{2}, \frac{3\pi}{2}]. 

Their sign values, however, are the opposite on each of these intervals. But, since tangent is equal to sine divided by cosine, its sign is the same over each of these two intervals. The sign of sine and the sign of cosine will still either be the same as each other (resulting in a positive tangent) or opposite to each other (resulting in a negative tangent).

Examples

This section goes over common examples of problems involving tangent graphs and their step-by-step solutions.

Example 1

Find the intervals over which the tangent graph is positive and negative on the segment $[0, 3\pi]$. 

Solution

To find these intervals, it helps to find the intervals over which sine is positive and over which cosine is positive.

Recall the mnemonic “All Students Take Calculus.” This means that all of the functions are positive in the first quadrant of the unit circle. Then, sine is positive in the second, tangent is positive in the third, and cosine is positive in the fourth.

The mnemonic says outright that tangent is positive in the third quadrant. This represents angles between $\pi$ and $\frac{3\pi}{2}$. Additionally, since all of the functions are positive in the first quadrant, tangent must be positive there. These are the angles between $0$ radians and $\frac{\pi}{2}$ radians.

Although sine is positive in the second quadrant, cosine is not. Therefore, all of the tangent values will be equal to a positive number divided by a negative number, which will be negative. Similarly, tangent is negative in the fourth quadrant where cosine is positive but sine is negative.

Therefore, the tangent is negative on the interval $(\frac{\pi}{2}, \pi)$, which is the second quadrant, and $(\frac{3\pi}{2}, 2\pi)$, which is the fourth quadrant.

Example 2

What is the period of a transformed tangent function of the form $y=tan(bx)$?

Solution

Like sine and cosine, the period of a transformed tangent function is the original period length divided by the coefficient of $x$. Since, in this case, the initial period is $\pi$, the new period will be $\frac{\pi}{b}$.

Example 3

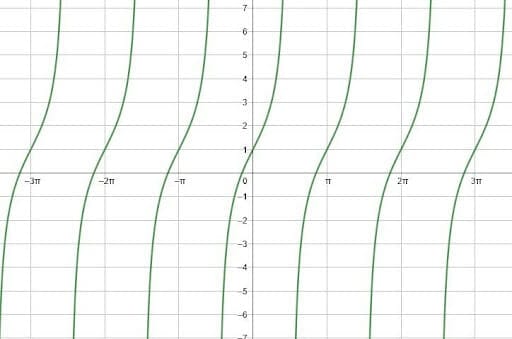
Graph the tangent function $y=2tan(x)+1$.

Solution

This function has a vertical shift of $+1$. This means that the flat part of the function will cross the line $y=1$ instead of the x-axis. 

Additionally, the function has a vertical stretch by a factor of $2$. Thus, all of the tangent values are multiplied by $2$, and the function will grow to infinity and minus infinity more quickly. 

The graph will look like this.

Example 4

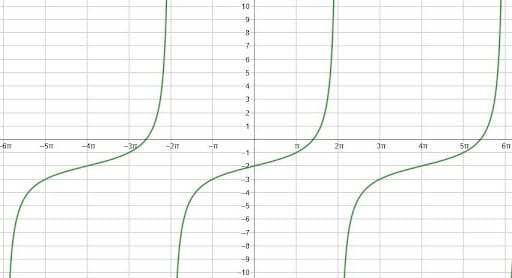
What is the equation for the tangent function shown?

Solution

First, note that there has been a vertical shift in this function. The flattened part of the graph that normally passes through the x-axis crosses the line $y=-2$. This means that there is a vertical shift of $-2$.

Then, note that the period of the function is different. In fact, from one vertical asymptote to another is $4\pi$. Since the period of a transformed function $y=tan(bx)$ is $\frac{\pi}{b}$, $b$ is equal to $\frac{\pi}{4\pi)$. This simplifies to $\frac{1}{4}$.

Therefore, the equation of the function is $y=tan(\frac{1}{4}x)-2$.

Example 5

How is the graph of the function $y=tan(x-\pi)$ different from the graph of the function $y=tanx$?

Solution

These functions will actually be the same.

Since $\pi$ is inside the parentheses, the function shifts $\pi$ radians to the right. But, since the function is $\pi$ periodic, the value $\pi$ radians to the right is the same. Thus, there will be no difference in the appearance of the graphs.