Trigonometric Ratios – Explanation and Examples

Trigonometric ratios are the ratios of certain sides in a right triangle given an angle measure.

These trigonometric ratios are the trigonometric functions sine, cosine, tangent, and their inverses. Each function represents a different ratio in a right triangle given an angle measure.

Trigonometric ratios are important in trigonometry, geometry, and all branches of physical science and engineering.  Before we go ahead with explaining the elements of this section, make sure to review trigonometric functions.

What Are Trigonometric Ratios?

Trigonometric ratios are ratios of the sides of a right triangle given one of the non-right angles of the triangle. Recall that a right triangle always has one right angle with a measure of $90$ degrees or $\frac{\pi}{2}$ radians. Therefore, knowing one of the other angles means the third angle is also known.

Since all triangles have $180$ degrees or $\pi$ radians, the measure of the third angle is equal to $180-90-\alpha$ degrees or $\pi-\frac{\pi}{2}-\alpha$ radians, where $\alpha$ is the measure of the known angle. These formulas simplify to $90-\alpha$ degrees and $\frac{\pi}{2}-\alpha$ radians. 

Trigonometric Functions

Knowing the angles of a triangle is not enough information to determine its side lengths. But, it is enough information to determine the ratio of each side to the others. This is where trigonometric functions come in. Recall that trigonometric (or “trig”) functions have an angle measure as an input and a ratio as an output. This input angle is the known non-right angle in a right triangle.

The ratio found with sine is the length of the opposite leg relative to the hypotenuse. That is, sine equals opposite divided by hypotenuse. Cosine is the ratio of the adjacent leg to the hypotenuse, and tangent is the ratio of the opposite leg over the adjacent leg.

Here, the “opposite leg” is the leg that does not form part of the angle. The hypotenuse is the leg across from the right angle, and the “adjacent leg” is the leg that, together with the hypotenuse, makes up the given angle. 

Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively. They are therefore hypotenuse over opposite, hypotenuse over adjacent, and adjacent over opposite.

Remembering Ratios

There is a simple mnemonic used to remember which trig function gives which angle ratio. It is “SOHCAHTOA.” (Pronounced “sockatowa”)

Here, S means sine, and the letters following it are O and H. Therefore, sine is opposite over hypotenuse.

Similarly, since A and H follow C, cosine is adjacent over the hypotenuse.

Finally, since O and A follow T, the tangent is opposite over adjacent.

Then, just recall that cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.

Relationship Between Ratios

Knowing either sine or cosine is enough to determine the other five trigonometric ratios.

There is a simple trig identity that helps with this. In particular, $sin^2\theta + cos^2\theta = 1$ for all angle measures $\theta$ in degrees or radians.

Therefore, knowing either sine or cosine and this identity allows one to solve for the other. From there, tangent is equal to sine divided by cosine. Then, the other trigonometric ratios are reciprocals of these three.

How To Find Trigonometric Ratios

There are several ways to find trigonometric ratios; one option is using a calculator, but this masks the math behind the ratio, and another option is to analyze particular triangles. For example, an isosceles right triangle has two $45$ degree angles (or two $\frac{\pi}{4}$ radians angles). 

Now, consider such a triangle on the unit circle. Since the Pythagorean Theorem holds for all right triangles, the triangle will have two legs of length $1$ and a hypotenuse of length $\sqrt{1^2+1^2} = \sqrt{2}$. 

Generalizing this for an isosceles triangle with a side length of $a$, the hypotenuse will have a length of $\sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}$.

Now, it is possible to look at the trigonometric ratios for this triangle.

The tangent is easiest because for either $45$ degree angle, the opposite is $a$ and the adjacent is $a$. Therefore, the ratio is $1$.

Since sine is opposite over hypotenuse, the sine will be $\frac{a}{a\sqrt{2}}$, which simplifies to $\frac{1}{\sqrt{2}}$.

Finally, cosine is adjacent over the hypotenuse. Therefore, it is also $\frac{a}{a\sqrt{2}} = \frac{1}{\sqrt{2}}$.

This triangle, along with a 30-60-90 triangle and a few trig identities, establishes a method for finding the trig ratios without a calculator.

Examples

This section goes over common examples of trigonometric ratios and their step-by-step solutions.

Example 1

The sine of a particular angle is $\frac{1}{5}$. What is the secant of the angle?

Solution

Since $sin\theta = \frac{1}{5}$ and secant is the reciprocal of cosine, it is necessary to use the identity $sin^2\theta + cos^2\theta = 1$ to find cosine first.

$(\frac{1}{5})^2=\frac{1}{25}$.

$1-\frac{1}{25} = \frac{24}{25}$.

The square root of this is $\frac{2\sqrt{6}}{5}$.

Then, the secant is $\frac{5}{2\sqrt{6}}$.

Example 2

What is the sine of angle $ABC$? What is the cosine of angle $ABC$? 

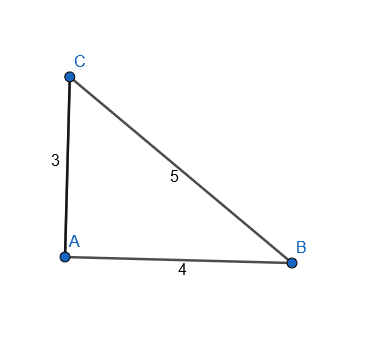
Solution

In this case, the side lengths are given. Therefore, one can just plug these values into the ratios. 

Since sine is opposite over hypotenuse and the side of length $3$ is opposite $ABC$, the sine is $\frac{3}{5}$.

Similarly, cosine is adjacent over hypotenuse. Therefore, cosine is $\frac{4}{5}$.

Example 3

Use limits to make a prediction about what happens to the cosine as $ABC$ goes to a right angle ($90$ degrees or $\frac{\pi}{2}$ radians).

Solution

As the angle $ABC$ gets larger and larger, the adjacent angle stays the same. All the while, the hypotenuse increases in length. 

Therefore, the ratio will get smaller and smaller. For example, if the adjacent side has a length of $1$ and the hypotenuse is $10$, the ratio of cosine is $\frac{1}{10}$. When the angle lengthens and the hypotenuse becomes $100$, the ratio is $\frac{1}{100}$. When the angle gets even longer and the hypotenuse has length $10,000$, the cosine will be $\frac{1}{10,000}$.

Therefore, the ratio gets closer and closer to $0$ as the angle gets larger and larger.

Example 4

Simplify the trig ratio represented by $\frac{sec}{tan}$.

Solution

$\frac{sec}{tan} = \frac{\frac{1}{cos}}{\frac{sin}{cos}} = \frac{1}{cos}\times\frac{cos}{sin} = \frac{cos}{cos\times sin} = \frac{1}{sin}$.

This is the reciprocal of sine, the cosecant.

Example 5

Use the fact that, in a 30-60-90 triangle, the hypotenuse is twice as long as the shorter side to find the three main trigonometric ratios for $30$ and $60$ degrees.

Hint: The shorter side is adjacent to the $60$ degree angle.

Solution

Start with the $60$ degree angle.

Here, the adjacent side is half of the hypotenuse. That is, $\frac{a}{h} = \frac{1}{2}$. Therefore, the cosine is $\frac{1}{2}$.

Using the identity $sin^2\theta + cos^2\theta = 1$, the sine of $60$ is $\frac{\sqrt{3}}{2}$.

This means that tangent is $\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}$.

Then consider the other angle. The shorter side is opposite this angle, so the sine is $\frac{1}{2}$. 

Therefore, the cosine is $\frac{\sqrt{3}}{2}$ and the tangent is $\frac{1}{\sqrt{3}}$.