They are a subset of real numbers, which exclude negative numbers, decimals, and fractions. Whole numbers include counting numerals as well. Whole numbers are defined as natural numbers plus zero (0). We are aware that the term “natural numbers” refers to a group of counting numbers beginning with 1, 2, 3, 4, and so on.

Whole numbers are a collection of numbers that don’t contain any fractions, decimals, or even negative integers. It is made up of zero and positive integers. Alternately, we may define whole numbers as the collection of non-negative integers. The inclusion of zero in the set of whole numbers marks the main distinction between them and natural numbers. Figure 1 illustrates the real line of whole numbers.

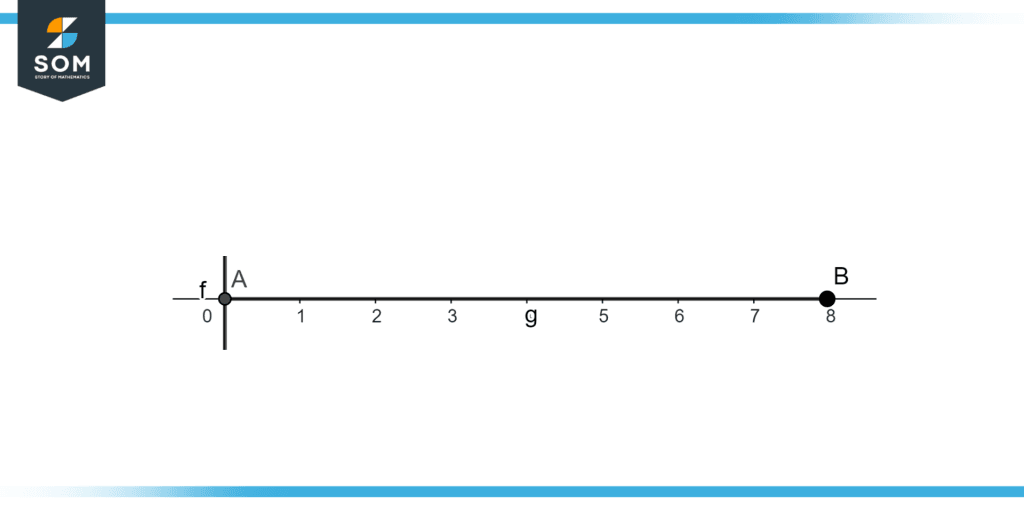
Figure 1 – Whole numbers on the real line

Whole numbers are a kind of natural numbers that include the number 0. The letter W stands for the set of whole integers in mathematics, which are 0 through 9.

Due to the fact that whole numbers begin at 0, 0 is the lowest whole number (from the definition of whole numbers). On a number line, zero sits in the middle of the positive and negative numbers. Although it has no value, zero is employed as a stand-in. In light of this, zero is a number that cannot be either positive or negative.

We realize that a characteristic number is any entire number that isn’t zero. All regular numbers are entire numbers, as well. The set of whole numbers is therefore a subset of the set of natural numbers. Natural numbers are a subset of the whole number set, as shown in Figure 2.

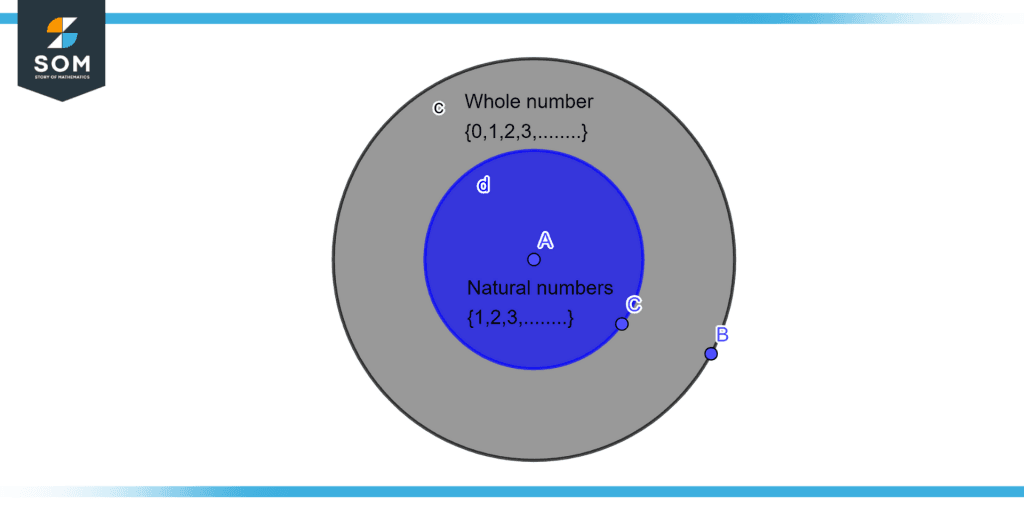
Figure 2 – Natural numbers and whole numbers as sets.

There is no biggest whole number, which is an intriguing aspect of the entire set of numbers. B + 1 is a whole number if b is the highest whole number. However, b + 1 is bigger than b. This method demonstrates that a larger whole number is always possible to find.

Difference between Whole numbers and Natural number

The complete set of all whole numbers is W = [0, 1, 2, 3,…]. The smallest total number is zero. A natural number is any whole number. The natural number range is given by N = 1, 2, 3, etc. 1. It is the lowest natural number. Except for 0, every whole number is a natural number.

Properties of the Whole number

Mathematical operations including combining, subtracting, dividing, and multiplying form the foundation of complete number characteristics. Two whole numbers can be joined, added, or subtracted to make the whole number. As a result, using the division method, we may also obtain a fraction. Here are some of the characteristics of whole numbers.

• Closure Property
• Associative Property
• Commutative Property
• Distributive Property

Closure Property

A whole number is always the result of two whole numbers when they are added and multiplied together.

Associative Property

The product or sum of any three whole numbers remains the same regardless of the numbers’ order.

Commutative Property

Even after changing the numbers’ order, the total and product of two whole numbers stay the same. According to this feature, the value of the total is unaffected by changes in the sequence of addition. A and B should be two entire numbers. A + B Equals B + A, according to the commutative property.

Distributive Property

According to this characteristic, a whole number’s multiplication is dispersed throughout the sum or difference of the whole numbers. It indicates that if two numbers, such as a and b, are multiplied by the same number c, and then added, the result may be obtained by multiplying the total of a and b by c. The formula for this attribute is: a (b + c) = (axb) + (axc).

Further Properties

Additive Identity

If w is a whole number, then w + 0 equals w, and w + 0 equals w. This means that adding a whole number to 0 has no effect on its value.

Multiplicative Identity

If w is a whole number, then w $\times$ 1 equals w. Thus, the multiplicative identity of all whole numbers is unity (1).

Multiplication of the Whole Number With Zero

When a whole number is multiplied by zero the result will be zero.

Division of the Whole Number With Zero

When a whole number is divided by zero the result will be undefined.

A whole number cannot be considered “large.” There is either a number immediately preceding or immediately preceding every value. There is only a percentage or decimal for two whole numbers; there is no whole number. There is no natural number zero; It’s an entire number. There are five initial whole numbers: 0, 1, 2, 3, and 4. Zero is the lowest entire number. Unless they can be reduced to a natural number or whole number, negative integers, fractions, and decimals are not natural numbers or whole numbers.

Some Examples of Whole Numbers

Example 1

Identify whether {-2,-1,0,1,2} are whole numbers.

Solution

The set of the whole number starts from zero and whole numbers are always non-negative since the first two elements of the set are -1 and -2 and they are negative so {-2,-1,0,1,2} are not a set of whole numbers.

Example 2

Add three whole numbers 20, 30, and 40 using the associative property of Whole numbers.

Solution

By using the associative property, we have:

• First Method

20 + (30 + 40)

= 20 + 70

= 90

• Second Method

(20 + 30) + 40

= 50 + 40

= 90

• Third Method

(20 + 40) + 30

= 60 + 30

= 90

Example 3

Solve 7(5+3) using the distributive property.

Solution

By the distributive property a (b+c)=a(b)+a(c) we have

 By distributive property 7(5+3) can be written as

7(5) + 7(3)

= 35 + 21

= 56

Example 4

Express the set {0,1,2,3,4,5} on the real line.

Solution

As {0,1,2,3,4,5} includes zero, and are positive so set is a whole number and figure 3 illustrates the real line of whole numbers.

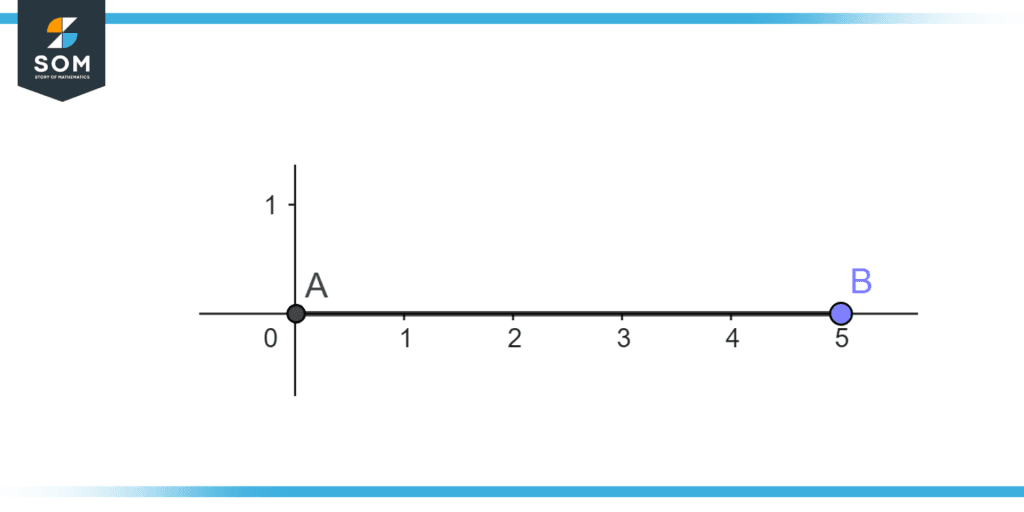
Figure 3 – Whole numbers from 0 to 5 on the real line.

All images/mathematical drawings were created using GeoGebra.

Whole Definition < Glossary Index > Width Definition