20TH CENTURY MATHEMATICS
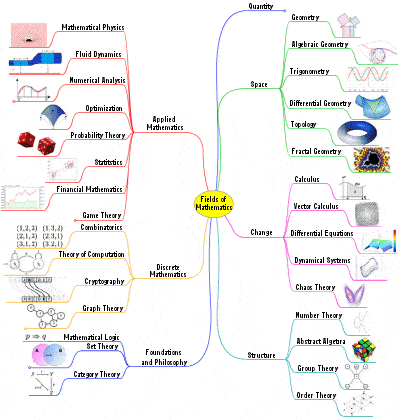 |
Fields of Mathematics |
The 20th Century continued the trend of the 19th towards increasing generalization and abstraction in mathematics, in which the notion of axioms as “self-evident truths” was largely discarded in favour of an emphasis on such logical concepts as consistency and completeness.
It also saw mathematics become a major profession, involving thousands of new Ph.D.s each year and jobs in both teaching and industry, and the development of hundreds of specialized areas and fields of study, such as group theory, knot theory, sheaf theory, topology, graph theory, functional analysis, singularity theory, catastrophe theory, chaos theory, model theory, category theory, game theory, complexity theory and many more.
The eccentric British mathematician G.H. Hardy and his young Indian protégé Srinivasa Ramanujan, were just two of the great mathematicians of the early 20th Century who applied themselves in earnest to solving problems of the previous century, such as the Riemann hypothesis. Although they came close, they too were defeated by that most intractable of problems, but Hardy is credited with reforming British mathematics, which had sunk to something of a low ebb at that time, and Ramanujan proved himself to be one of the most brilliant (if somewhat undisciplined and unstable) minds of the century.
Others followed techniques dating back millennia but taken to a 20th Century level of complexity. In 1904, Johann Gustav Hermes completed his construction of a regular polygon with 65,537 sides (216 + 1), using just a compass and straight edge as Euclid would have done, a feat that took him over ten years.
The early 20th Century also saw the beginnings of the rise of the field of mathematical logic, building on the earlier advances of Gottlob Frege, which came to fruition in the hands of Giuseppe Peano, L.E.J. Brouwer, David Hilbert and, particularly, Bertrand Russell and A.N. Whitehead, whose monumental joint work the “Principia Mathematica” was so influential in mathematical and philosophical logicism.
 |
Part of the transcript of Hilbert’s 1900 Paris lecture, in which he set out his 23 problems |
The century began with a historic convention at the Sorbonne in Paris in the summer of 1900 which is largely remembered for a lecture by the young German mathematician David Hilbert in which he set out what he saw as the 23 greatest unsolved mathematical problems of the day. These “Hilbert problems” effectively set the agenda for 20th Century mathematics, and laid down the gauntlet for generations of mathematicians to come. Of these original 23 problems, 10 have now been solved, 7 are partially solved, and 2 (the Riemann hypothesis and the Kronecker-Weber theorem on abelian extensions) are still open, with the remaining 4 being too loosely formulated to be stated as solved or not.
Hilbert was himself a brilliant mathematician, responsible for several theorems and some entirely new mathematical concepts, as well as overseeing the development of what amounted to a whole new style of abstract mathematical thinking. Hilbert‘s approach signalled the shift to the modern axiomatic method, where axioms are not taken to be self-evident truths. He was unfailingly optimistic about the future of mathematics, famously declaring in a 1930 radio interview “We must know. We will know!”, and was a well-loved leader of the mathematical community during the first part of the century.
However, the Austrian Kurt Gödel was soon to put some very severe constraints on what could and could not be solved, and turned mathematics on its head with his famous incompleteness theorem, which proved the unthinkable – that there could be solutions to mathematical problems which were true but which could never be proved.
Alan Turing, perhaps best known for his war-time work in breaking the German enigma code, spent his pre-war years trying to clarify and simplify Gödel’s rather abstract proof. His methods led to some conclusions that were perhaps even more devastating than Gödel’s, including the idea that there was no way of telling beforehand which problems were provable and which unprovable. But, as a spin-off, his work also led to the development of computers and the first considerations of such concepts as artificial intelligence.
With the gradual and wilful destruction of the mathematics community of Germany and Austria by the anti-Jewish Nazi regime in the 1930 and 1940s, the focus of world mathematics moved to America, particularly to the Institute for Advanced Study in Princeton, which attempted to reproduce the collegiate atmosphere of the old European universities in rural New Jersey. Many of the brightest European mathematicians, including Hermann Weyl, John von Neumann, Kurt Gödel and Albert Einstein, fled the Nazis to this safe haven.
Emmy Noether, a German Jew who was also forced out of Germany by the Nazi regime, was considered by many (including Albert Einstein) to be the most important woman in the history of mathematics. Her work in the 1920s and 1930s changed the face of abstract algebra, and she made important contributions in the fields of algebraic invariants, commutative rings, number fields, non-commutative algebra, and hypercomplex numbers. Noether’s theorem on the connection between symmetry and conservation laws was key in the development of quantum mechanics and other aspects of modern physics.
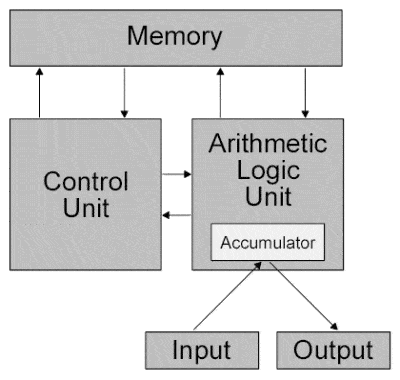 |
Von Neumann’s computer architecture design |
John von Neumann is considered one of the foremost mathematicians in modern history, another mathematical child prodigy who went on to make major contributions to a vast range of fields. In addition to his physical work in quantum theory and his role in the Manhattan Project and the development of nuclear physics and the hydrogen bomb, he is particularly remembered as a pioneer of game theory, and particularly for his design model for a stored-program digital computer that uses a processing unit and a separate storage structure to hold both instructions and data, a general architecture that most electronic computers follow even today.
Another American, Claude Shannon, has become known as the father of information theory, and he, von Neumann and Alan Turing between them effectively kick-started the computer and digital revolution of the 20th Century. His early work on Boolean algebra and binary arithmetic resulted in his foundation of digital circuit design in 1937 and a more robust exposition of communication and information theory in 1948. He also made important contributions in cryptography, natural language processing and sampling theory.
The Soviet mathematician Andrey Kolmogorov is usually credited with laying the modern axiomatic foundations of probability theory in the 1930s, and he established a reputation as the world’s leading expert in this field. He also made important contributions to the fields of topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity.
André Weil was another refugee from the war in Europe, after narrowly avoiding death on a couple of occasions. His theorems, which allowed connections to be made between number theory, algebra, geometry and topology, are considered among the greatest achievements of modern mathematics. He was also responsible for setting up a group of French mathematicians who, under the secret nom-de-plume of Nicolas Bourbaki, wrote many influential books on the mathematics of the 20th Century.
Perhaps the greatest heir to Weil’s legacy was Alexander Grothendieck, a charismatic and beloved figure in 20th Century French mathematics. Grothendieck was a structuralist, interested in the hidden structures beneath all mathematics, and in the 1950s he created a powerful new language which enabled mathematical structures to be seen in a new way, thus allowing new solutions in number theory, geometry, even in fundamental physics. His “theory of schemes” allowed certain of Weil‘s number theory conjectures to be solved, and his “theory of topoi” is highly relevant to mathematical logic. In addition, he gave an algebraic proof of the Riemann-Roch theorem, and provided an algebraic definition of the fundamental group of a curve. Although, after the 1960s, Grothendieck all but abandoned mathematics for radical politics, his achievements in algebraic geometry have fundamentally transformed the mathematical landscape, perhaps no less than those of Cantor, Gödel and Hilbert, and he is considered by some to be one of the dominant figures of the whole of 20th Century mathematics.
Paul Erdös was another inspired but distinctly non-establishment figure of 20th Century mathematics. The immensely prolific and famously eccentric Hungarian mathematician worked with hundreds of different collaborators on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory. As a humorous tribute, an “Erdös number” is given to mathematicians according to their collaborative proximity to him. He was also known for offering small prizes for solutions to various unresolved problems (such as the Erdös conjecture on arithmetic progressions), some of which are still active after his death.
 |
The Mandelbrot set, the most famous example of a fractal |
The field of complex dynamics (which is defined by the iteration of functions on complex number spaces) was developed by two Frenchmen, Pierre Fatou and Gaston Julia, early in the 20th Century. But it only really gained much attention in the 1970s and 1980s with the beautiful computer plottings of Julia sets and, particularly, of the Mandelbrot sets of yet another French mathematician, Benoît Mandelbrot. Julia and Mandelbrot fractals are closely related, and it was Mandelbrot who coined the term fractal, and who became known as the father of fractal geometry.
The Mandelbrot set involves repeated iterations of complex quadratic polynomial equations of the form zn+1 = zn2 + c, (where z is a number in the complex plane of the form x + iy). The iterations produce a form of feedback based on recursion, in which smaller parts exhibit approximate reduced-size copies of the whole, and which are infinitely complex (so that, however much one zooms in and magifies a part, it exhibits just as much complexity).
Paul Cohen is an example of a second generation Jewish immigrant who followed the American dream to fame and success. His work rocked the mathematical world in the 1960s, when he proved that Cantor‘s continuum hypothesis about the possible sizes of infinite sets (one of Hilbert’s original 23 problems) could be both true AND not true, and that there were effectively two completely separate but valid mathematical worlds, one in which the continuum hypothesis was true and one where it was not. Since this result, all modern mathematical proofs must insert a statement declaring whether or not the result depends on the continuum hypothesis.
Another of Hilbert’s problems was finally resolved in 1970, when the young Russian Yuri Matiyasevich finally proved that Hilbert’s tenth problem was impossible, i.e. that there is no general method for determining when polynomial equations have a solution in whole numbers. In arriving at his proof, Matiyasevich built on decades of work by the American mathematician Julia Robinson, in a great show of internationalism at the height of the Cold War.
In additon to complex dynamics, another field that benefitted greatly from the advent of the electronic computer, and particulary from its ability to carry out a huge number of repeated iterations of simple mathematical formulas which would be impractical to do by hand, was chaos theory. Chaos theory tells us that some systems seem to exhibit random behaviour even though they are not random at all, and conversely some systems may have roughly predictable behaviour but are fundamentally unpredictable in any detail. The possible behaviours that a chaotic system may have can also be mapped graphically, and it was discovered that these mappings, known as “strange attractors“, are fractal in nature (the more you zoom in, the more detail can be seen, although the overall pattern remains the same).
An early pioneer in modern chaos theory was Edward Lorenz, whose interest in chaos came about accidentally through his work on weather prediction. Lorenz’s discovery came in 1961, when a computer model he had been running was actually saved using three-digit numbers rather than the six digits he had been working with, and this tiny rounding error produced dramatically different results. He discovered that small changes in initial conditions can produce large changes in the long-term outcome – a phenomenon he described by the term “butterfly effect” – and he demonstrated this with his Lorenz attractor, a fractal structure corresponding to the behaviour of the Lorenz oscillator (a 3-dimensional dynamical system that exhibits chaotic flow).
 |
Example of a four-colour map |
1976 saw a proof of the four colour theorem by Kenneth Appel and Wolfgang Haken, the first major theorem to be proved using a computer. The four colour conjecture was first proposed in 1852 by Francis Guthrie (a student of Augustus De Morgan), and states that, in any given separation of a plane into contiguous regions (called a “map”) the regions can be coloured using at most four colours so that no two adjacent regions have the same colour. One proof was given by Alfred Kempe in 1879, but it was shown to be incorrect by Percy Heawood in 1890 in proving the five colour theorem. The eventual proof that only four colours suffice turned out to be significantly harder. Appel and Haken’s solution required some 1,200 hours of computer time to examine around 1,500 configurations.
Also in the 1970s, origami became recognized as a serious mathematical method, in some cases more powerful than Euclidean geometry. In 1936, Margherita Piazzola Beloch had shown how a length of paper could be folded to give the cube root of its length, but it was not until 1980 that an origami method was used to solve the “doubling the cube” problem which had defeated ancient Greek geometers. An origami proof of the equally intractible “trisecting the angle” problem followed in 1986. The Japanese origami expert Kazuo Haga has at least three mathematical theorems to his name, and his unconventional folding techniques have demonstrated many unexpected geometrical results.
The British mathematician Andrew Wiles finally proved Fermat’s Last Theorem for ALL numbers in 1995, some 350 years after Fermat’s initial posing. It was an achievement Wiles had set his sights on early in life and pursued doggedly for many years. In reality, though, it was a joint effort of several steps involving many mathematicians over several years, including Goro Shimura, Yutaka Taniyama, Gerhard Frey, Jean-Pierre Serre and Ken Ribet, with Wiles providing the links and the final synthesis and, specifically, the final proof of the Taniyama-Shimura Conjecture for semi-stable elliptic curves. The proof itself is over 100 pages long.
The most recent of the great conjectures to be proved was the Poincaré Conjecture, which was solved in 2002 (over 100 years after Poincaré first posed it) by the eccentric and reclusive Russian mathematician Grigori man. However, Perelman, who lives a frugal life with his mother in a suburb of St. Petersburg, turned down the $1 million prize, claiming that “if the proof is correct then no other recognition is needed”. The conjecture, now a theorem, states that, if a loop in connected, finite boundaryless 3-dimensional space can be continuously tightened to a point, in the same way as a loop drawn on a 2-dimensional sphere can, then the space is a three-dimensional sphere. Perelman provided an elegant but extremely complex solution involving the ways in which 3-dimensional shapes can be “wrapped up” in even higher dimensions. Perelman has also made landmark contributions to Riemannian geometry and geometric topology.
John Nash, the American economist and mathematician whose battle against paranoid schizophrenia has recently been popularized by the Hollywood movie “A Beautiful Mind”, did some important work in game theory, differential geometry and partial differential equations which have provided insight into the forces that govern chance and events inside complex systems in daily life, such as in market economics, computing, artificial intelligence, accounting and military theory.
The Englishman John Horton Conway established the rules for the so-called “Game of Life” in 1970, an early example of a “cellular automaton” in which patterns of cells evolve and grow in a grid, which became extremely popular among computer scientists. He has made important contributions to many branches of pure mathematics, such as game theory, group theory, number theory and geometry, and has also come up with some wonderful-sounding concepts like surreal numbers, the grand antiprism and monstrous moonshine, as well as mathematical games such as Sprouts, Philosopher’s Football and the Soma Cube.
Other mathematics-based recreational puzzles became even more popular among the general public, including Rubik’s Cube (1974) and Sudoku (1980), both of which developed into full-blown crazes on a scale only previously seen with the 19th Century fads of Tangrams (1817) and the Fifteen puzzle (1879). In their turn, they generated attention from serious mathematicians interested in exploring the theoretical limits and underpinnings of the games.
Computers continue to aid in the identification of phenomena such as Mersenne primes numbers (a prime number that is one less than a power of two – see the section on 17th Century Mathematics). In 1952, an early computer known as SWAC identified 2257-1 as the 13th Mersenne prime number, the first new one to be found in 75 years, before going on to identify several more even larger.
 |
Approximations for π |
With the advent of the Internet in the 1990s, the Great Internet Mersenne Prime Search (GIMPS), a collaborative project of volunteers who use freely available computer software to search for Mersenne primes, has led to another leap in the discovery rate. Currently, the 13 largest Mersenne primes were all discovered in this way, and the largest (the 45th Mersenne prime number and also the largest known prime number of any kind) was discovered in 2009 and contains nearly 13 million digits. The search also continues for ever more accurate computer approximations for the irrational number π, with the current record standing at over 5 trillion decimal places.
The P versus NP problem, introduced in 1971 by the American-Canadian Stephen Cook, is a major unsolved problem in computer science and the burgeoning field of complexity theory, and is another of the Clay Mathematics Institute’s million dollar Millennium Prize problems. At its simplest, it asks whether every problem whose solution can be efficiently checked by a computer can also be efficiently solved by a computer (or put another way, whether questions exist whose answer can be quickly checked, but which require an impossibly long time to solve by any direct procedure). The solution to this simple enough sounding problem, usually known as Cook’s Theorem or the Cook-Levin Theorem, has eluded mathematicians and computer scientists for 40 years. A possible solution by Vinay Deolalikar in 2010, claiming to prove that P is not equal to NP (and thus such insolulable-but-easily-checked problems do exist), has attracted much attention but has not as yet been fully accepted by the computer science community.
The Chinese-born American mathematician, Yitang Zhang, working in the area of number theory, achieved perhaps the most significant result since Perelman, when he provided a proof of the first finite bound on gaps between prime numbers in 2013.
<< Back to Poincaré | Forward to Hardy and Ramanujan >> |
