19TH CENTURY MATHEMATICS
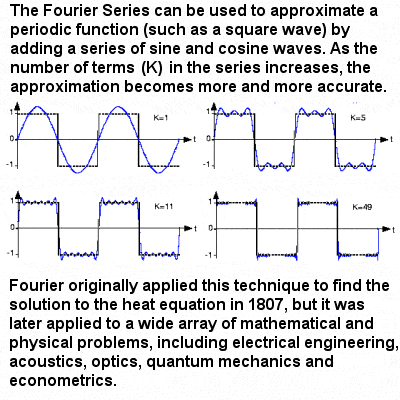 |
Approximation of a periodic function by the Fourier Series |
The 19th Century saw an unprecedented increase in the breadth and complexity of mathematical concepts. Both France and Germany were caught up in the age of revolution which swept Europe in the late 18th Century, but the two countries treated mathematics quite differently.
After the French Revolution, Napoleon emphasized the practical usefulness of mathematics and his reforms and military ambitions gave French mathematics a big boost, as exemplified by “the three L’s”, Lagrange, Laplace and Legendre (see the section on 18th Century Mathematics), Fourier and Galois.
Joseph Fourier’s study, at the beginning of the 19th Century, of infinite sums in which the terms are trigonometric functions were another important advance in mathematical analysis. Periodic functions that can be expressed as the sum of an infinite series of sines and cosines are known today as Fourier Series, and they are still powerful tools in pure and applied mathematics. Fourier (following Leibniz, Euler, Lagrange and others) also contributed towards defining exactly what is meant by a function, although the definition that is found in texts today – defining it in terms of a correspondence between elements of the domain and the range – is usually attributed to the 19th Century German mathematician Peter Dirichlet.
In 1806, Jean-Robert Argand published his paper on how complex numbers (of the form a + bi, where i is √-1) could be represented on geometric diagrams and manipulated using trigonometry and vectors. Even though the Dane Caspar Wessel had produced a very similar paper at the end of the 18th Century, and even though it was Gauss who popularized the practice, they are still known today as Argand Diagrams.
The Frenchman Évariste Galois proved in the late 1820s that there is no general algebraic method for solving polynomial equations of any degree greater than four, going further than the Norwegian Niels Henrik Abel who had, just a few years earlier, shown the impossibility of solving quintic equations, and breaching an impasse which had existed for centuries. Galois‘ work also laid the groundwork for further developments such as the beginnings of the field of abstract algebra, including areas like algebraic geometry, group theory, rings, fields, modules, vector spaces and non-commutative algebra.
Germany, on the other hand, under the influence of the great educationalist Wilhelm von Humboldt, took a rather different approach, supporting pure mathematics for its own sake, detached from the demands of the state and military. It was in this environment that the young German prodigy Carl Friedrich Gauss, sometimes called the “Prince of Mathematics”, received his education at the prestigious University of Göttingen. Some of Gauss’ ideas were a hundred years ahead of their time, and touched on many different parts of the mathematical world, including geometry, number theory, calculus, algebra and probability. He is widely regarded as one of the three greatest mathematicians of all times, along with Archimedes and Newton.
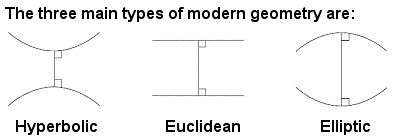 |
Euclidean, hyperbolic and elliptic geometry |
Later in life, Gauss also claimed to have investigated a kind of non-Euclidean geometry using curved space but, unwilling to court controversy, he decided not to pursue or publish any of these avant-garde ideas. This left the field open for János Bolyai and Nikolai Lobachevsky (respectively, a Hungarian and a Russian) who both independently explored the potential of hyperbolic geometry and curved spaces.
The German Bernhard Riemann worked on a different kind of non-Euclidean geometry called elliptic geometry, as well as on a generalized theory of all the different types of geometry. Riemann, however, soon took this even further, breaking away completely from all the limitations of 2 and 3 dimensional geometry, whether flat or curved, and began to think in higher dimensions. His exploration of the zeta function in multi-dimensional complex numbers revealed an unexpected link with the distribution of prime numbers, and his famous Riemann Hypothesis, still unproven after 150 years, remains one of the world’s great unsolved mathematical mysteries and the testing ground for new generations of mathematicians.
British mathematics also saw something of a resurgence in the early and mid-19th century. Although the roots of the computer go back to the geared calculators of Pascal and Leibniz in the 17th Century, it was Charles Babbage in 19th Century England who designed a machine that could automatically perform computations based on a program of instructions stored on cards or tape. His large “difference engine” of 1823 was able to calculate logarithms and trigonometric functions, and was the true forerunner of the modern electronic computer. Although never actually built in his lifetime, a machine was built almost 200 years later to his specifications and worked perfectly. He also designed a much more sophisticated machine he called the “analytic engine“, complete with punched cards, printer and computational abilities commensurate with modern computers.
Another 19th Century Englishman, George Peacock, is usually credited with the invention of symbolic algebra, and the extension of the scope of algebra beyond the ordinary systems of numbers. This recognition of the possible existence of non-arithmetical algebras was an important stepping stone toward future developments in abstract algebra.
In the mid-19th Century, the British mathematician George Boole devised an algebra (now called Boolean algebra or Boolean logic), in which the only operators were AND, OR and NOT, and which could be applied to the solution of logical problems and mathematical functions. He also described a kind of binary system which used just two objects, “on” and “off” (or “true” and “false”, 0 and 1, etc), in which, famously, 1 + 1 = 1. Boolean algebra was the starting point of modern mathematical logic and ultimately led to the development of computer science.
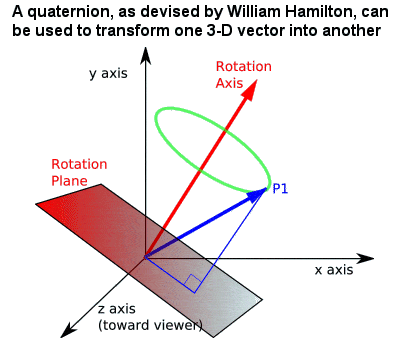 |
Hamilton’s quaternion |
The concept of number and algebra was further extended by the Irish mathematician William Hamilton, whose 1843 theory of quaternions (a 4-dimensional number system, where a quantity representing a 3-dimensional rotation can be described by just an angle and a vector). Quaternions, and its later generalization by Hermann Grassmann, provided the first example of a non-commutative algebra (i.e. one in which a x b does not always equal b x a), and showed that several different consistent algebras may be derived by choosing different sets of axioms.
The Englishman Arthur Cayley extended Hamilton’s quaternions and developed the octonions. But Cayley was one of the most prolific mathematicians in history, and was a pioneer of modern group theory, matrix algebra, the theory of higher singularities, and higher dimensional geometry (anticipating the later ideas of Klein), as well as the theory of invariants.
Throughout the 19th Century, mathematics in general became ever more complex and abstract. But it also saw a re-visiting of some older methods and an emphasis on mathematical rigour. In the first decades of the century, the Bohemian priest Bernhard Bolzano was one of the earliest mathematicians to begin instilling rigour into mathematical analysis, as well as giving the first purely analytic proof of both the fundamental theorem of algebra and the intermediate value theorem, and early consideration of sets (collections of objects defined by a common property, such as “all the numbers greater than 7” or “all right triangles“, etc). When the German mathematician Karl Weierstrass discovered the theoretical existence of a continuous function having no derivative (in other words, a continuous curve possessing no tangent at any of its points), he saw the need for a rigorous “arithmetization” of calculus, from which all the basic concepts of analysis could be derived.
Along with Riemann and, particularly, the Frenchman Augustin-Louis Cauchy, Weierstrass completely reformulated calculus in an even more rigorous fashion, leading to the development of mathematical analysis, a branch of pure mathematics largely concerned with the notion of limits (whether it be the limit of a sequence or the limit of a function) and with the theories of differentiation, integration, infinite series and analytic functions. In 1845, Cauchy also proved Cauchy’s theorem, a fundamental theorem of group theory, which he discovered while examining permutation groups. Carl Jacobi also made important contributions to analysis, determinants and matrices, and especially his theory of periodic functions and elliptic functions and their relation to the elliptic theta function.
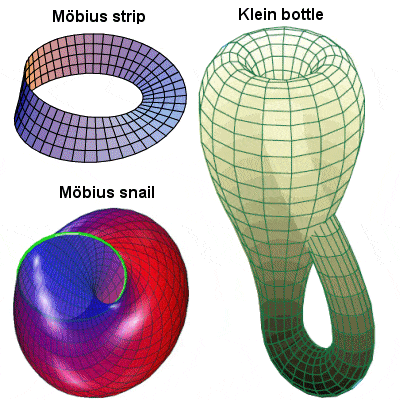 |
Non-orientable surfaces with no identifiable “inner” and “outer” sides |
August Ferdinand Möbius is best known for his 1858 discovery of the Möbius strip, a non-orientable two-dimensional surface which has only one side when embedded in three-dimensional Euclidean space (actually a German, Johann Benedict Listing, devised the same object just a couple of months before Möbius, but it has come to hold Möbius’ name). Many other concepts are also named after him, including the Möbius configuration, Möbius transformations, the Möbius transform of number theory, the Möbius function and the Möbius inversion formula. He also introduced homogeneous coordinates and discussed geometric and projective transformations.
Felix Klein also pursued more developments in non-Euclidean geometry, include the Klein bottle, a one-sided closed surface that cannot be embedded in three-dimensional Euclidean space, only in four or more dimensions. It can be best visualized as a cylinder looped back through itself to join with its other end from the “inside”. Klein’s 1872 Erlangen Program, which classified geometries by their underlying symmetry groups (or their groups of transformations), was a hugely influential synthesis of much of the mathematics of the day, and his work was very important in the later development of group theory and function theory.
The Norwegian mathematician Marius Sophus Lie also applied algebra to the study of geometry. He largely created the theory of continuous symmetry, and applied it to the geometric theory of differential equations by means of continuous groups of transformations known as Lie groups.
In an unusual occurrence in 1866, an unknown 16-year old Italian, Niccolò Paganini, discovered the second smallest pair of amicable numbers (1,184 and 1210), which had been completely overlooked by some of the greatest mathematicians in history (including Euler, who had identified over 60 such numbers in the 18th Century, some of them huge).
In the later 19th Century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity, and which has since become the common language of nearly all mathematics. In the face of fierce resistance from most of his contemporaries and his own battle against mental illness, Cantor explored new mathematical worlds where there were many different infinities, some of which were larger than others.
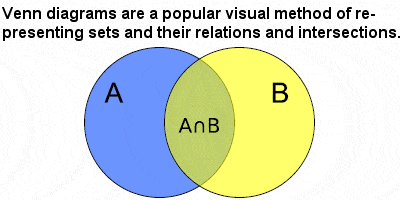 |
Venn diagram |
Cantor’s work on set theory was extended by another German, Richard Dedekind, who defined concepts such as similar sets and infinite sets. Dedekind also came up with the notion, now called a Dedekind cut which is now a standard definition of the real numbers. He showed that any irrational number divides the rational numbers into two classes or sets, the upper class being strictly greater than all the members of the other lower class. Thus, every location on the number line continuum contains either a rational or an irrational number, with no empty locations, gaps or discontinuities. In 1881, the Englishman John Venn introduced his “Venn diagrams” which become useful and ubiquitous tools in set theory.
Building on Riemann’s deep ideas on the distribution of prime numbers, the year 1896 saw two independent proofs of the asymptotic law of the distribution of prime numbers (known as the Prime Number Theorem), one by Jacques Hadamard and one by Charles de la Vallée Poussin, which showed that the number of primes occurring up to any number x is asymptotic to (or tends towards) x⁄log x.
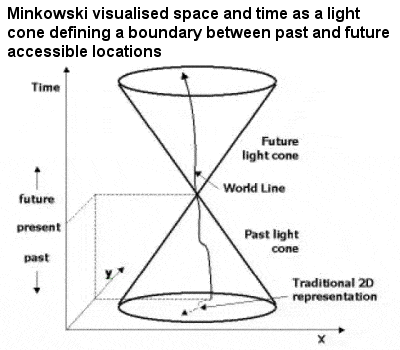 |
Minkowski space-time |
Hermann Minkowski, a great friend of David Hilbert and teacher of the young Albert Einstein, developed a branch of number theory called the “geometry of numbers” late in the 19th Century as a geometrical method in multi-dimensional space for solving number theory problems, involving complex concepts such as convex sets, lattice points and vector space. Later, in 1907, it was Minkowski who realized that the Einstein’s 1905 special theory of relativity could be best understood in a four-dimensional space, often referred to as Minkowski space-time.
Gottlob Frege’s 1879 “Begriffsschrift” (roughly translated as “Concept-Script”) broke new ground in the field of logic, including a rigorous treatment of the ideas of functions and variables. In his attempt to show that mathematics grows out of logic, he devised techniques that took him far beyond the logical traditions of Aristotle (and even of George Boole). He was the first to explicitly introduce the notion of variables in logical statements, as well as the notions of quantifiers, universals and existentials. He extended Boole‘s “propositional logic” into a new “predicate logic” and, in so doing, set the stage for the radical advances of Giuseppe Peano, Bertrand Russell and David Hilbert in the early 20th Century.
Henri Poincaré came to prominence in the latter part of the 19th Century with at least a partial solution to the “three body problem”, a deceptively simple problem which had stubbornly resisted resolution since the time of Newton, over two hundred years earlier. Although his solution actually proved to be erroneous, its implications led to the early intimations of what would later become known as chaos theory. In between his important work in theoretical physics, he also greatly extended the theory of mathematical topology, leaving behind a knotty problem known as the Poincaré conjecture which remined unsolved until 2002.
Poincaré was also an engineer and a polymath, and perhaps the last of the great mathematicians to adhere to an older conception of mathematics, which championed a faith in human intuition over rigour and formalism. He is sometimes referred to as the “Last Univeralist” as he was perhaps the last mathematician able to shine in almost all of the various aspects of what had become by now a huge, encyclopedic and incredibly complex subject. The 20th Century would belong to the specialists.
<< Back to Euler | Forward to Galois >> |
