- Home
- >
- Calculus
Calculus
Calculus is the study of things in motion or things that are changing. It uses concepts from algebra, geometry, trigonometry, and precalculus. The word itself comes from a Latin word meaning “pebble” because pebbles used to be used in calculations.
Calculus has applications in both engineering and business because of its usefulness in optimization.
For example, an engineer could use calculus to find out the least amount of material needed for a machine to still operate correctly. Alternatively, a human resource director can use it to figure out the minimum number of employees needed for a new site to operate.
Calculus is often divided up as calculus I, II, and III.
Calculus I will typically cover both differential and integral calculus like this guide.
Calculus II explores more complex topics of integral calculus and series and sequences, while calculus III is normally the study of multi-variable calculus.
Alternatively, many high schools in the United States break calculus up as calculus AB and calculus BC. Calculus AB will cover the equivalent of calculus I while calculus BC will cover most of calculus I and II.
 Although Isaac Newton generally gets the credit “inventing” or “discovering” calculus, the concepts of calculus were derived independently by Isaac Newton and Gottfried Wilhelm Leibnitz at about the same time. For Newton, calculus was necessary for describing the physics of gravity that he was simultaneously studying.
Although Isaac Newton generally gets the credit “inventing” or “discovering” calculus, the concepts of calculus were derived independently by Isaac Newton and Gottfried Wilhelm Leibnitz at about the same time. For Newton, calculus was necessary for describing the physics of gravity that he was simultaneously studying.
This guide mainly focuses on the topics learned in calculus I. It begins with an in-depth explanation of differential calculus, including limits, the product and quotient rules, the chain rule, derivatives of different functions, and optimization.
The second section deals with integral calculus, including Riemann sums, the fundamental theorem of calculus, indefinite integrals, and different methods for calculating integrals.
The final section explores the concepts of polar coordinates and parametric equations that are often covered at the end of calculus courses.
Differential Calculus
Differential calculus is concerned with rates of change and motion. It can be used to calculate the rate of change of a curve at any particular point or find the maxima or minima of curves. The functions used to derive these values are called “derivatives.” For example, the first derivative of any function can be used to find a line tangent to a curve at any given point. In the image, the line that is tangent to the function e^x at the point (0,1) is y=x+1.
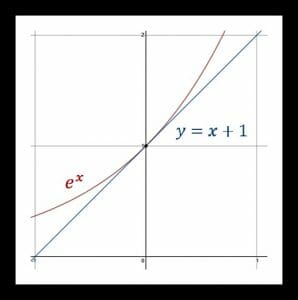
Newton and Leibnitz used the concept of a limit to find the derivative of a function. Once one learns the derivatives of common functions, one can use certain rules to find the derivates of more complicated functions.
This section begins with an introduction to calculus, limits, and derivatives. It then introduces rules for finding derivatives including the power rule, product rule, quotient rule, and chain rule.
The guide also includes resources for finding the derivatives of different types of functions, including trigonometric and logarithmic functions. Next, there are resources explaining how to take derivatives of derivates and the applications of that.
Finally, the topic ends with a discussion of optimization and more advanced differential calculus subtopics.
- Introduction to Calculus
- The Limits of a Function
- Derivatives
- Power Rule
- Product Rule
- Quotient Rule
- Chain Rule
- Derivative Rules
- Trigonometric Derivatives
- Inverse Trigonometric Derivatives
- Trigonometric Substitution
- Deriving the Derivative Formulas for Trigonometric Functions
- Derivatives of Exponential Functions
- Derivative of the Natural Log
- Logarithmic Differentiation
- Implicit Differentiation
- Second Derivative and Higher Derivatives
- Maxima and Minima
- Finding Critical Numbers
- Concavity
- Sketching Curves
- Mean Value Theorem
- Asymptotes
- Hyperbolic Functions
- L’Hopital’s Rule
- Optimization with Derivatives
- Related Rates with Derivatives
- Newton’s Method
Integral Calculus
Integral calculus makes up of the second half of the first part of calculus. It is essentially a way of working backwards from derivatives. That is, rather than finding the derivative of a function, one finds which function or functions a derivative corresponds to.
Whereas the derivative can be used to calculate the rate of change on a curve at any given point, an integral can be used to find the area under a curve over any interval. The relationship between integrals and derivatives forms the backbone of the fundamental theorem of calculus, which will be discussed in detail in this topic.
The relationship between integrals and areas under curves is best explained through Riemann sums, which are loosely illustrated in the image below.
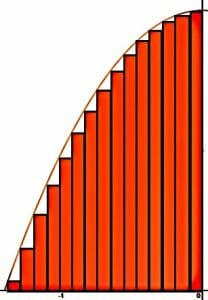
Note that the area under this curve can be nearly approximated by the sum of the area of the rectangles. If the width of the rectangles were smaller, the approximation would be even closer. This is discussed in more thoroughly in the subtopic about Riemann sums.
This guide first discusses antiderivatives, definite integrals, and methods for approximating definite integrals. It then introduces and explains the fundamental theorem of calculus. After that, the exploration of integrals continues with different methods that can be used for integration and how to integrate different functions such as exponential and hyperbolic functions. Finally, the topic ends with an exploration of more advanced topics in integral calculus.
- Antiderivative
- Definite Integral
- Approximating Integrals using Rectangles, the Trapezoid Rule, and Simpson’s Rule
- Calculating Definite Integrals with Riemann Sums
- The Fundamental Theorem of Calculus
- Indefinite Integrals
- Improper Integrals
- Integration by Parts
- Integration using U-Substitution
- Integration using Partial Fractions
- Integrating Exponential Functions
- Integrating Hyperbolic Functions
- Trigonometric Integrals
- Integration using Inverse Trigonometric Functions
- Integral Test
- Area under a Curve
- Centroids and Center of Mass
- Volume of Revolution
- Laplace Transform
- Inverse Laplace Transform
Parametric Curves and Polar Coordinates
Precalculus courses often introduce the topics of parametric curves and polar coordinates. Most calculus courses discuss them in more detail and explain how derivatives and integrals work with both parametric curves and polar coordinates.

This guide also explains the relationship between parametric curves and calculus and polar coordinates and calculus. It begins with a review of parametric curves before introducing how to find integrals and derivates for them.
It then reviews polar coordinates and explains how calculus can be used to find the rate of change and area under curves in the polar coordinate system.
The guide ends with a review of the graphs of polar curves.
